Fonction exponentielle : cours de maths en 1ère en PDF.

La fonction exponentielle à travers un cours de maths en 1ère sur ses propriétés et sa définition. Nous étudierons sa fonction dérivée, sa courbe représentative et ses variations.Ainsi que, ses limites aux bornes de son ensemble de définition.

I. Définition et variations de la fonction exponentielle.

Définition :

Soit un réel strictement positif.

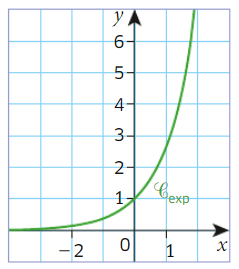
Une fonction f définie pour tout réel $x\in\,[0;+\infty[$ par est une fonction exponentielle.

Propriété :

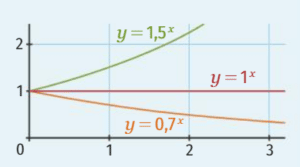
Une fonction exponentielle f définie sur $[0;+\infty[$ par avec >0 est :

strictement croissante sur $[0;+\infty[$ si, et seulement si, >1;
strictement décroissante sur $[0;+\infty[$ si, et seulement si, 0 < < 1;
constante sur $[0;+\infty[$ si, et seulement si, = 1.

II. Les propriétés algébriques de la fonction exponentielle.

Propriétés :

Pour tous réels positifs et et pour tous réels strictement positifs et , on a :

$a^x\times \,a^y=a^{x+y}$ ;
$\frac{a^x}{a^y}=a^{x-y}$ ;
$(a^x)^y=a^{x\times \,y}$ ;
$a^x\times \,b^x=(a\times \,b)^x$ ;
$\frac{a^x}{b^x}=\,(\,\frac{a}{b}\,\,)^x$ .

Propriété : cas de la puissance $\frac{1}{n}$ .

Soient et deux nombres réels strictement positifs et un nombre entier non nul.

L’équation x^n=a admet comme unique solution positive le réel $x=\sqrt[n]{a}$ = $a^{\frac{1}{n}}$ appelée racine n-ième de .

Propriété :

Si une grandeur subit une évolution de taux , alors elle atteint la même valeur en subissant évolutions successives de même taux $(1+t)^{\frac{1}{n}}-1$ où un nombre entier naturel non nul.

Définition:

Le nombre $(1+t)^{\frac{1}{n}}-1$ est appelé taux moyen des évolutions successives de taux global .

Télécharger puis imprimer cette fiche en PDF.

Télécharger ou imprimer cette fiche «fonction exponentielle : cours de maths en 1ère en PDF.» au format PDF afin de pouvoir travailler en totale autonomie.

Vous devez vous inscrire ou vous connecter à votre compte afin de pouvoir télécharger ce document au format PDF.