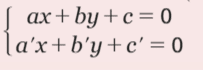équation de droites et orthogonalité: cours de maths en 1ère.

sommaire

1 I. Vecteurs directeurs et équation cartésienne
- 1.1 1.Vecteur directeur d’une droite.
- 1.2 2. Equation cartésienne de droite.
2 II. Positions relatives de droites

L’orthogonalité et les équations de droites à travers un cours de maths en 1ère. Nous utiliserons le produit scalaire pour les vecteurs normaux et les vecteurs colinéaires ainsi que, la détermination de l’équation réduite ou cartésienne d’une droite du plan.

I. Vecteurs directeurs et équation cartésienne

Dans tout ce chapitre, on se place dans un repère orthonormé $(O,\vec{i},\vec{j})$ .

1.Vecteur directeur d’une droite.

Définition :

On appelle vecteur directeur d’une droite (d) tout représentant du vecteur $\vec{AB}$ où

A et B sont deux points quelconques et distincts de la droite (d).

Exemple :

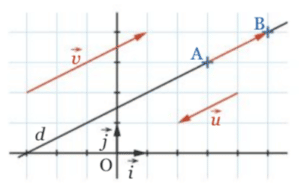
Dans l’image ci-dessous, les vecteurs $\vec{AB}(2;1)$ , $\vec{u}(-2;-1)$ et $\vec{v}(4;2)$ sont des vecteurs

directeurs de la droite (d).

Application et méthode :

On calcule les coordonnées d’un vecteur directeur de la droite.
La droite (BC) et sa parallèle ont les mêmes vecteurs directeurs, il suffi d’en prendre un représentant d’origine A.

Exemple :

Soient trois points A(1;5), B(-3;2) et C(2;-1) dans un repère orthonormé.

Déterminer un vecteur directeur de la droite (BC).
Détailler la construction de la parallèle à (BC) passant par A.

2. Equation cartésienne de droite.

Théorème :

Dans un repère orthonormé, les coordonnées de l’ensemble des points M(x;y)

d’une droite vérifient une relation où a, b et c sont des nombres réels.

Démonstration :

Soient et deux points d’une droite (d).

Alors, pour tout point appartenant à (d), nous avons :

les vecteurs $\vec{PM}(x-x_P;y-y_P)$ et $\vec{PQ}(x_Q-x_P;y_Q-y_P)$ sont colinéaires.

On a donc $det(\vec{PM};\vec{PQ})=0$ .

C’est-à-dire .

donc .

En posant ; et ,

on a donc l’équation de la droite (d) qui est de la forme .

Définition :

La relation s’appelle une équation cartésienne de la droite (d).

Propriété :

Le vecteur $\vec{u}(-b;a)$ est un vecteur directeur de la droite (d) d’équation cartésienne .

Exemple :

Si la droite (d) a pour équation cartésienne , alors le vecteur $\vec{u}(-4;5)$

est un vecteur directeur de cette droite.

II. Positions relatives de droites

1.Droites parallèles ou sécantes

Théorème :

Soient deux droites (d) et (d’) d’équations cartésiennes respectives et où sont des nombres réels.

Les droites (d) et (d’) sont parallèles si, et seulement si, $ab'-a'b\neq0$ .

Preuve :

Des vecteurs directeurs des droites (d) et (d’) sont, respectivement, $\vec{u}(-b;a)$ et $\vec{v}(-b';a')$ .

Les droites (d) et (d’) sont sécantes si, et seulement si, les vecteurs $\vec{u}$ et $\vec{v}$ ne sont pas colinéaires.

Autrement dit, si le déterminant de ces deux vecteurs est non nul.

Soit, $-ba'-(a(-b'))=-ba'+ab'=ab'-a'b\neq0$ .

2. Droites sécantes et systèmes d’équation

Théorème :

Lorsque deux droites sont sécantes, les coordonnées (x;y) de leur point d’intersection

sont solution du système :

3. Droites perpendiculaires

Théorème :

Soient deux droites (d) et (d’) d’équations cartésiennes respectives et où sont des nombres réels.

Les vecteurs directeurs des droites (d) et (d’) sont, respectivement, $\vec{u}(-b;a)$ et $\vec{v}(-b';a')$ .

Les droites (d) et (d’) sont perpendiculaires si, et seulement si, $\vec{u}.\vec{v}=0$ soit .

Preuve :

Les vecteurs directeurs des droites (d) et (d’) sont, respectivement, $\vec{u}(-b;a)$ et $\vec{v}(-b';a')$ .

Les droites sont perpendiculaires si, et seulement si, ces deux vecteurs directeurs sont orthogonaux.

Ce qui revient à dire que le produit scalaire de ces deux vecteurs est nul, soit :

$\vec{u}.\vec{v}=0$

Ce qui équivaut à :

$-b\times \,(-b')+a\times \,a'=0$ soit .

Télécharger puis imprimer cette fiche en PDF.

Télécharger ou imprimer cette fiche «orthogonalité et équations de droites : cours de maths en 1ère en PDF.» au format PDF afin de pouvoir travailler en totale autonomie.

Réviser les cours et exercices avec nos Q.C.M :

Q.C.M en 6ème Q.C.M en 5ème Q.C.M en 4ème Q.C.M en 3ème Q.C.M en 2de Q.C.M en 1ère Q.C.M en Terminale

D'autres ressources pour progresser en autonomie :

Chronomètre Horloge France Tables Multiplication Arrondir des décimaux Rapporteur et Angles Médiatrice Symétrie Axiale d'un triangle Symétrie Centrale d'un triangle Translation d'un triangle Rotation Homothétie Bissectrice Tracer droite parallèle Conversion Aires et Volumes Addition de deux relatifs Soustraction Relatifs Addition et soustraction de trois relatifs Produit Deux Relatifs Produit Trois Relatifs Quotient Relatifs Carré Entier Racine Carrée Théorème Pythagore Liste Diviseurs Décomposition Facteurs Premiers Calcul du PGCD PGCD Algorithme Euclide Test Nombre Premier Déterminer Fonction Linéaire Déterminer Fonction Affine Traceur Courbe Trigonométrie Angle Trigonométrie Longueur Périmètre d'un Cercle Aire d'un Disque Volume du Parallélépipède Rectangle Volume du cylindre Surface d'une Sphère et Volume d'une boule Volume d'une pyramide à base rectangulaire Section d'une pyramide Visualiser Section Cône en 2D Section d'un Cône Carte Mondiale Coordonnées Géographiques

Mathématiques Web c'est 2 250 077 fiches de cours et d'exercices téléchargées.