Suites numériques : exercices de maths en 1ère corrigés en PDF.

Les suites numériques à travers des exercices de maths en 1ère corrigés afin de réviser votre chapitre en ligne.

Vous retrouverez dans ces fiches les notions suivantes :

définition d’une suite numérique;
suite arithmétique;
terme de rang n d’une suite arithmétique et somme des premiers termes;
terme de rang n d’une suite géométrique et somme des premiers termes;
sens de variation d’une suite (croissante et décroissante ou monotone).

L’élève devra être capable de calculer le terme de rang n d’une suite ainsi que la somme de ses termes. Vous devrez savoir étudier son sens de variation et calculer sa limite en l’infini. Ces énoncés sont accompagnés de leur correction, ainsi, vous pourrez vous auto-corriger afin de combler vos lacunes en première.

Exercice 1 :

Soit la suite définie pour tout $n\in \mathbb{N}$ par .

Calculer et .

Exercice 2 :

Soit la suite définie pour tout $n\in \mathbb{N}$ par $u_n=\frac{n+1}{2n-3}$ .

Calculer et $u_{10}$ .

Exercice 3 :

On considère la suite définie pour tout $n\in \mathbb{N}$ par .

Exprimer $u_{n+1},u_{n-1},u_{2n}$ et en fonction de n.

Exercice 4 :

On considère la suite définie par et, pour tout $n\in \mathbb{N}$ , $u_{n+1}=\frac{2u_n-2}{u_n-3}$ .

1) Calculer et .

2)A l’aide de la calculatrice, donner une valeur approchée de $u_{15}$ à $10^{-2}$ près.

Exercice 5 :

Soit la suite définie pour tout $n\in \mathbb{N}$ par .

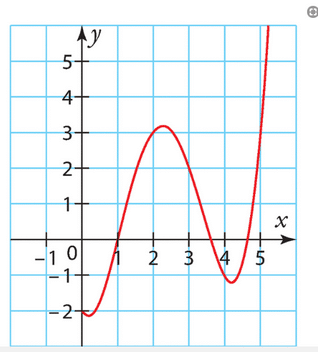
On donne ci-dessous la courbe représentative de la fonction f.

Déterminer la valeur des cinq premiers termes de la suite .

Exercice 6 :

Soit une suite arithmétique de raison 2 et de premier terme .

1)Exprimer en fonction de n.

2)Calculer $u_{20}$ .

Exercice 7 :

Les suites suivantes sont-elles arithmétiques ? Justifier.

a) définie par et, pour tout $n\in\mathbb{N},u_{n+1}=u_n-4$ .

b) définie pour tout $n\in \mathbb{N}$ par .

c) définie pour tout $n\in \mathbb{N}$ par .

Exercice 8 :

Les suites suivantes sont-elles géométriques ? Justifier.

a) définie par et, pour tout $n\in\mathbb{N},u_{n+1}=\frac{u_n}{2}$ .

b) définie pour tout $n\in \mathbb{N}$ par .

c) définie pour tout $n\in \mathbb{N}$ par $w_n=\frac{1}{4^n}$ .

Exercice 9 :

Yacine a préparé un gâteau au chocolat qu’il a déposé
dans une assiette dans la cuisine. À chaque fois qu’il passe
devant, il se sert la moitié de ce qui reste.

On note , la proportion du gâteau qui reste dans l’assiette
après que Yacine se soit servi n fois.

1. Donner la valeur de et de .

2. Justifier que la suite est une suite géométrique et préciser sa raison.

Exercice 10 :

En étudiant le signe de $u_{n+1}-u_n$ , étudier les variations des suites ,

définies pour tout $n\in \mathbb{N}$ .

$b)u_n=\frac{4}{n+1}$ .

Exercice 11 :

Soit la suite définie pour tout entier $n\geq\, 1$ par $u_n=\frac{2^n}{n}$ .

1)Calculer $\frac{u_{n+1}}{u_n}$ .

2)Résoudre l’inéquation $\frac{2n}{n+1}>1$ .

3)En déduire les variations de la suite .

Exercice 12 :

Yanis a une grande collection de poupées russes.

On s’intéresse à une série de poupées russes.

La plus petite figurine mesure 1 cm de hauteur.

Chaque poupée se trouve dans une poupée qui mesure 0,5 cm de plus qu’elle.

On note , la taille de la n-ième poupée (dans l’ordre croissant).
On a donc .

1. Exprimer en fonction de n.

2. Quelle est la taille de la 10° poupée ?

3. Si, au lieu d’emboîter les poupées on les empilait, quelle
serait la hauteur d’une pile formée de 10 poupées ?

Exercice 13 :

1.Soit la suite définie pour tout $n\in \mathbb{N}$ par .
Calculer , et .

2. Soit la suite définie tout $n\in \mathbb{N}$ par $u_n=\frac{n+1}{2n-3}$
Calculer et $u_{10}$ .

3. On considère la suite définie pour tout $n\in \mathbb{N}$ par .
Calculer les cinq premiers termes de la suite .

4. On considère la suite définie pour tout $n\in \mathbb{N}$ par .
Exprimer $u_{n+1};u_{n-1};u_{2n};u_{n}+1$ en fonction de n.

5. Soit la suite définie pour tout $n\in \mathbb{N}$ par .
Exprimer $u_{n+1};u_{n-1};u_{2n};u_{n}+1$ en fonction de n.

Exercice 14 :

Un matin, Mathéo décide de poser un récipient dans son jardin, contenant 200 g de noisettes.
Chaque après-midi, un écureuil vient manger la moitié du récipient, puis Mathéo remet 80 g
de noisettes le soir.
On note la quantité en grammes de noisettes dans le récipient le n-ième jour au matin.
1. Donner la valeur de et .
2. Exprimer $u_{n+l}$ en fonction de .

Exercice 15 :

Soit la suite définie pour tout $n\in \mathbb{N}$ par .
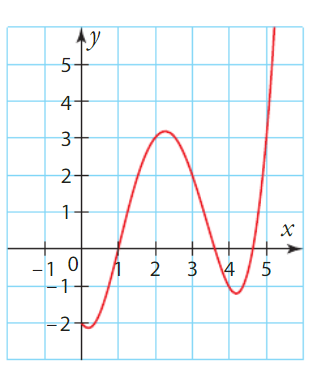
On donne ci-dessous la courbe représentative de la fonction f.
Déterminer la valeur des cinq premiers termes de la suite .

Exercice 16 :

Soit la suite définie par et, pour tout $n\in \mathbb{N}$ par $v_{n+1} = f(v_n)$ .
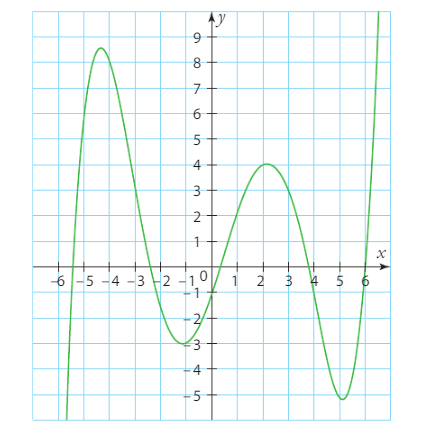
On donne ci-dessous la courbe représentative de la fonction f.
Déterminer la valeur des cinq premiers termes de la suite .

Exercice 17 :

Soit une suite arithmétique de raison 4 et de premier terme .
Calculer et .
Soit une suite arithmétique de raison 2 et de premier terme .
1.Exprimer en fonction de n.
2.Calculer $u_{20}$ .

Exercice 18 :

En étudiant le signe de $u_{n+1}- u_n$ , étudier les variations des suites définies pour tout $n \in \mathbb{N}.$

$a)u_n=n^2+2n\\b)u_n=\frac{4}{n+1}\\c)u_n=-5^n$

Exercice 19 :

Soit la suite définie pour tout entier $n\geq\, 1$ par $u_n=\frac{2^n}{n}$ .
1. Calculer $\frac{u_{n+1}}{u_n}$ .
2. Résoudre l’inéquation $\frac{2n}{n+1}>1$ .
3. En déduire les variations de la suite .

Exercice 20 :

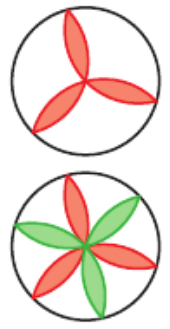
Étape O : Valentine trace une rosace à trois pétales.
Étape 1 : Elle décide de décorer davantage sa rosace et rajoute un pétale entre deux pétales
consécutifs.

A chaque étape, elle rajoute chaque fois un pétale entre deux pétales consécutifs.
On note le nombre de pétales l’étape n.
On a .
1. Tracer la rosace à l’étape 2.
2. En déduire la valeur de et .
3. Exprimer $u_{n+1}$ en fonction de .
4. En déduire l’expression de .

Exercice 21 :

On s’intéresse à une feuille de papier carrée de côté 20 cm.
A chaque étape, on replie les coins de cette feuille pour obtenir un nouveau carré.

On veut étudier la suite qui correspond à la longueur des côtés du carré à l’étape n, en cm.

On a .

1. Déterminer la valeur de .
2. Déterminer une relation entre et $u_{n+1}$ .
3. En déduire les variations de la suite .
4. Conjecturer la limite de la suite
On veut maintenant étudier la suite qui correspond à l’épaisseur du pliage, en m, à l’étape n.
La feuille de papier initiale a une épaisseur de 0,1 mm.
5. Déterminer la valeur de et de .
6. Déterminer une relation entre et $v_{n+1}$ .
7. En déduire les variations de la suite .
8. En déduire l’expression de en fonction de n.
9. A l’aide de la calculatrice, déterminer le nombre d’étapes qu’il faudrait pour que le pliage fasse la hauteur de la tour Eiffel, c’est-à-dire 324 m.

3.7/5 - (47 votes)

Télécharger puis imprimer cette fiche en PDF.

Télécharger ou imprimer cette fiche «suites numériques : exercices de maths en 1ère corrigés en PDF.» au format PDF afin de pouvoir travailler en totale autonomie.

D'autres cours et exercices à consulter

Mathématiques Web c'est 2 268 522 fiches de cours et d'exercices téléchargées.