Equation et inéquations du second degré : exercices en 1ère.

Les équations et les inéquations du second degré à une inconnue à travers des exercices de maths en 1ère corrigés. Cette fiche permet à l’élève de bien réviser et il aura l’occasion de s’entraîner davantage sur des énoncés à difficultés variables. Vous devrez savoir calculer la valeur du discriminant et déterminer les racines ainsi que savoir mettre en place le tableau de signe. L’objectif est de savoir résoudre une équation ou une inéquation du second degré par le calcul ou graphiquement. Vous retrouverez les notions suivantes :

forme canonique;
méthode de résolution avec le discriminant delta;
résolution d’une inéquation du second degré à une inconnue;
résolution d’une inéquation par la méthode graphique.

Ces ressources disposent de leur correction pour que vous puissiez voir vos erreurs et ils peuvent être téléchargés ou imprimés en PDF en première.

Exercice 1 :

Résoudre dans $\mathbb{R}$ les équations suivantes.

2) Soit f la fonction définie sur $\mathbb{R}$ par .

Déterminer le nombres de solutions réelles de l’équation f(x)=0.

Exercice 2 :

déterminer la ou les éventuelles racines des fonctions suivantes.

$b)g(x)=x^2+x+\frac{1}{4}.$

2) Déterminer toutes les solutions réelles des équations suivantes.

Exercice 3 :

Soit f la fonction définie sur $\mathbb{R}$ par $f(x)=-7x^2-\frac{49}{2}x+14$ .

déterminer le nombre de racines de la fonction f, en justifiant.
Vérifier que – 4 est une racine de f.
En utilisant la somme ou le produit des racines, déterminer la valeur de l’autre racine.

Exercice 4 :

Pour chaque fonction ci-dessous, déterminer si c’est une fonction polynôme de degré 2.

$a)f(x)=x^2+2x-\sqrt{2}$ .

$b)g(x)=x^2+\frac{1}{x}-1$ .

Exercice 5 :

Soit f la fonction définie sur $\mathbb{R}$ par .

1)Développer l’expression .

2)En déduire la forme canonique de f.

Exercice 6 :

Déterminer la forme canonique des fonctions suivantes.

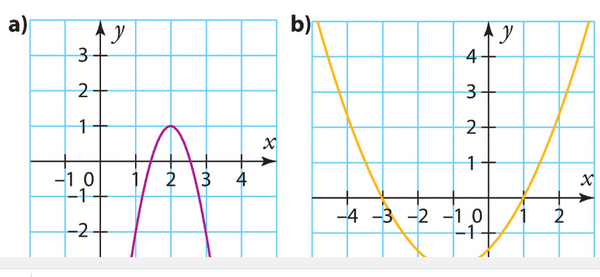
Exercice 7 :

Pour chaque fonction représentée ci-dessous,

déterminer les coordonnées du sommet, l’axe de symétrie et le signe de .

Exercice 8 :

Pour chaque équation de parabole donnée ci-dessous,

déterminer son axe de symétrie et les coordonnées du sommet.

Exercice 9 :

Factoriser les expressions suivantes, en utilisant des identités remarquables.

Exercice 10 :

Pour chaque trinôme ci-dessous, calculer le discriminant $\Delta$ .

Exercice 11 :

Résoudre dans $\mathbb{R}$ les équations suivantes.

$c)2x^2-2x+\frac{1}{2}=0.$

Exercice 12 :

Résoudre dans $\mathbb{R}$ les inéquations suivantes sans utiliser le discriminant.

$b)x^2-81\leq\, 0.$

Exercice 13 :

Soit f une fonction polynôme de degré 2 définie sur $\mathbb{R}$ par
, avec $a\neq 0$ .

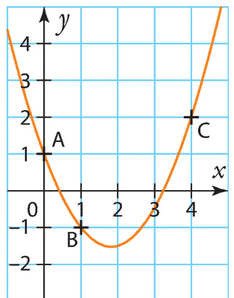
La courbe représentative de f est donnée ci-dessous.

1. À l’aide des coordonnées du point A, déterminer la valeur de c.
2. À l’aide des coordonnées des points B et C, déterminer la valeur
des coefficients a et b.

3. En déduire l’expression de f(x) en fonction de x.

Exercice 14 :

Pour chaque trinôme ci-dessous, calculer le discriminant $\Delta$ .

Exercice 15 :

Déterminer le nombre de solutions réelles de chaque équation ci-dessous.

$c)-\frac{1}{3}x^2+2x-3=0$

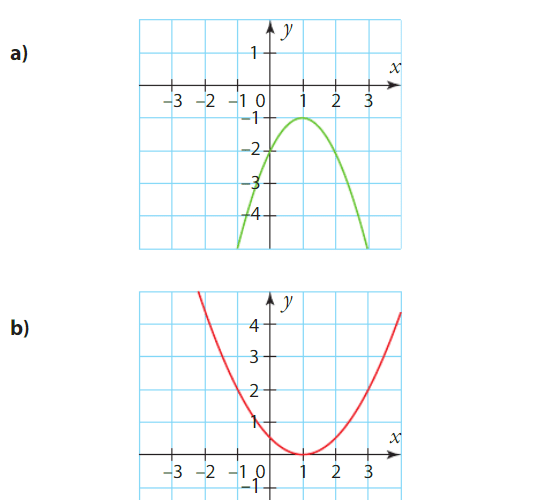
Exercice 16 :

Pour chaque trinôme représenté graphiquement ci-dessous, déterminer le signe de $\Delta$ .

Exercice 17 :

Dresser le tableau de signes de chaque fonction définie ci-dessous.

Exercice 18 :

Résoudre dans $\mathbb{R}$ les inéquations suivantes sans utiliser le discriminant.

$b)x^2-81\leq\, 0$

Exercice 19 :

Résoudre dans $\mathbb{R}$ les inéquations suivantes.
$a) 3x^2 -4x+\frac{4}{3}\leq\, 0$

Déterminer l’ensemble des solutions réelles des inéquations suivantes.
$a)-6x^2+ 15x-4 \leq\, 2$

Exercice 20 :

Soit fla fonction définie sur $\mathbb{R}$ par .
1. Déterminer la forme canonique de f, en utilisant les identités remarquables.
2. Déterminer la forme factorisée de f, en utilisant les identités remarquables.
3. En utilisant la forme adaptée, résoudre :

$a) f(x)=0\\ b) f(x)=-27\\ c) f(x)=-36$

4.Soit g la fonction définie sur $\mathbb{R}$ par $g(x) = 2x^2-\frac{3}{2}x-\frac{1}{2}$ .
a) Vérifier que 1 est racine de g.
b) En utilisant la somme ou le produit des racines déterminer la valeur de l’autre racine de g.
5.Résoudre f(x) < g(x).

4.3/5 - (24 votes)

Télécharger puis imprimer cette fiche en PDF.

Télécharger ou imprimer cette fiche «equations et inéquations du second degré : exercices de maths en 1ère corrigés en PDF.» au format PDF afin de pouvoir travailler en totale autonomie.

D'autres cours et exercices à consulter

Mathématiques Web c'est 2 268 522 fiches de cours et d'exercices téléchargées.