Probabilités : cours de maths en 1ère à télécharger en PDF.

Sommaire de cette fiche

Les probabilités à travers un cours de maths en 1ère à télécharger gratuitement au format pdf.

I. Calculer des fréquences

Définition :

Dans une série statistique à deux variables (ou série statistique bivariée), les valeurs sont généralement représentées dans un tableau croisé d’effectifs.
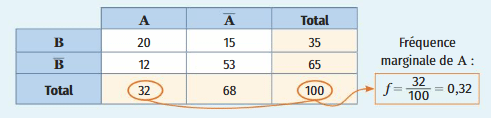
Les sommes des lignes et des colonnes d’un tableau double entrée sont appelées les marges du tableau.
Elles apparaissent en jaune dans le tableau ci-dessous.
La fréquence marginale d’une valeur est le quotient de l’effectif total de cette valeur par l’effectif total.

Remarque :

On parle de fréquence marginale car on utilise uniquement les nombres situés dans la marge du tableau.

Exemple :
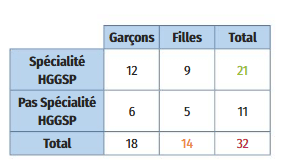
On considère une classe de première constituée de 32 élèves ayant choisi ou non la spécialité HGGSP.
Sur l’ensemble des 32 élèves de la classe, 21 ont choisi la spécialité HGGSP.

La fréquence marginale de la valeur « spécialité HGGSP » est donc $\frac{21}{32}$ .
Sur l’ensemble des 32 élèves de la classe, 14 sont des filles.
La fréquence marginale de la valeur « filles » est donc égale à $\frac{14}{32}$ soit 43,75 %.

Définition :

Lorsque l’on cherche la fréquence d’apparition de la valeur A uniquement pour une sous-population non
vide B de la série statistique, on dit que l’on calcule la fréquence conditionnelle de la valeur A parmi B.
Cette fréquence conditionnelle, notée f_B(A) , est égale à $f_B(A)=\frac{effectif\,verifiant\,a\,la\,fois\,A\,parmi\,B}{effectif\,de\,B}$ .

Remarque :

On parle de fréquence conditionnelle car on calcule la fréquence d’une valeur en imposant une condition.

Exemple :
On reprend l’exemple ci-dessus et on cherche connaitre la fréquence de filles (valeur A) parmi les élèves
n’ayant pas choisi la spécialité HGGSP (sous-population B).

Dans le tableau, on lit qu’il y a 5 filles qui n’ont pas choisi la spécialité HGGSP sur un total de 11 élèves qui ne suivent pas cette spécialité.
5
Ainsi, $f_B(A)=\frac{5}{11}\simeq 0,455$ .

Parmi les élèves qui ne sont pas inscrits en HGGSP, il y a environ 45,5 % de filles.

II. Calculer des probabilités

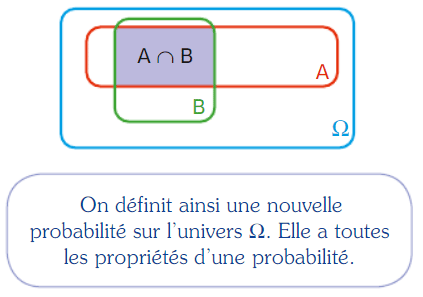
Soit A et B deux événements d’un même univers de probabilité non nulle.

Définition :

La probabilité conditionnelle que l’événement B se réalise sachant que l’événement A s’est déjà réalisé se note P_A (B) et est définie par $P_A (B)=\frac{P(A\cap B)}{P(A)}$ .

Exemple :

On reprend l’exemple précédent. On choisit un élève de la classe au hasard et on considère les événements :
A : « L’élève a choisi la spécialité HGGSP » et B : « L’élève est un garçon ».

On utilise le tableau pour trouver $P_A (B)=\frac{12}{21}=\frac{4}{7}$ .

La probabilité de choisir un garçon sachant que l’élève choisi suit la spécialité HGGSP est de $\frac{4}{7}$ .

Définition :

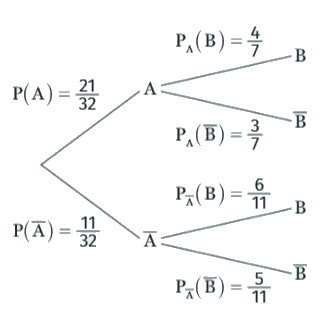
Lorsqu’on réalise une expérience aléatoire mettant en jeu plusieurs événements, il est plus facile d’organiser les différentes issues en utilisant un arbre de probabilités.

La première série de branche sépare les issues selon la réalisation du premier événement.

La deuxième série de branche selon le deuxième événement, etc.
On indique sur chaque branche de l’arbre la probabilité correspondante comme indiquée sur l’arbre ci-dessous.
Les probabilités du deuxième niveau de l’arbre sont des probabilités conditionnelles.

Propriétés :

1. Dans un arbre de probabilité, la somme des probabilités sur les branches issues d’un même noeud est
égale à 1.
2. On appelle chemin une suite de branches décrivant une succession d’événements. La probabilité d’un
chemin est égale au produit des probabilités situées sur les branches qui le composent.
3.La probabilité d’un événement est la somme des probabilités des chemins qui y aboutissent.

Définition :

Les événements A et B sont dits indépendants lorsque ou, de manière symétrique, lorsque .

Remarque :

Intuitivement, cela signifie que la probabilité que B se réalise ne dépend pas de la réalisation de l’événement A.

Exemple :

En conservant le même exemple, on observe que $P_B(A)= \frac{12}{18}=\frac{2}{3}$ et $P(A)=\frac{21}{32}$ .
On en déduit que les événements A et B ne sont pas indépendants.

5/5 - (4 votes)

Télécharger puis imprimer cette fiche en PDF.

Télécharger ou imprimer cette fiche «probabilités : cours de maths en 1ère en PDF.» au format PDF afin de pouvoir travailler en totale autonomie.

D'autres cours et exercices à consulter

Mathématiques Web c'est 2 268 189 fiches de cours et d'exercices téléchargées.