Produit scalaire : cours de maths en 1ère à télécharger en PDF.

Sommaire de cette fiche

Le produit scalaire à travers un cours de maths en 1ère qui est à télécharger gratuitement au format PDF . Ainsi, il fait intervenir respectivement les notions suivantes :

– définition:

– norme d’un vecteur;

– cosinus et produit scalaire;

– vecteurs orthogonaux;

– bilinéarité du produit scalaire;

– symétrie;

– équation cartésienne et réduite d’une droite;

– équation d’un cercle.

I. Norme d’un vecteur

Propriétés :

Soit $\vec{u}$ un vecteur de coordonnées ( ; ) dans une base orthonormée du plan.

a. On appelle norme du vecteur $\vec{u}$ , notée $\| \vec{u} \|$ , le nombre $\| \vec{u} \|=\sqrt{x^2+y^2}$ .

b. Si est un nombre réel, alors $\| k\vec{u} \|= | k |\times \| \vec{u} \|$ .

II. Critère d’orthogonalité de deux vecteurs

Définition :

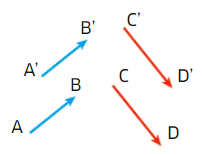
Soient $\vec{u}$ et $\vec{v}$ deux vecteurs non nuls de représentants respectifs $\vec{AB}$ et $\vec{CD}$ .
Les vecteurs $\vec{u}$ et $\vec{v}$ sont orthogonaux lorsque les droites (AB) et (CD) sont perpendiculaires.

On note dans ce cas $\vec{u}\perp \vec{v}$ .

Remarque :

La définition ne dépend pas des représentants des vecteurs.
En effet, Si $\vec{AB} =\vec{A'B'}$ et $\vec{CD} =\vec{C'D'}$ et que $(AB)\perp (CD)$ alors $(A'B')\perp (C'D')$ .

Propriété :

Soient $\vec{u}$ et $\vec{v}$ deux vecteurs non nuls
Les vecteurs $\vec{u}$ et $\vec{v}$ sont orthogonaux si, et seulement si, $\| \vec{u}+\vec{v} \|^2= \| \vec{u} \|^2+ \| \vec{v} \|^2$ (1).

Remarques :

L’égalité (1) provient du théorème de Pythagore.

L’égalité (1) est encore vérifiée si un des deux vecteurs est nul.
Ainsi, on considère que le vecteur nul $\vec{0}$ et $\vec{v}$ sont orthogonaux ou encore que $\vec{0}$ est orthogonal à tous les vecteurs du plan.

Propriété :

Soient $\vec{u}$ et $\vec{v}$ deux vecteurs de coordonnées respectives (X ; Y) et (X’ ; Y’)
dans une base orthonormée du plan.
Les vecteurs $\vec{u}$ et $\vec{v}$ sont orthogonaux si et seulement si .

Démonstration :

D’après la propriété précédente, les vecteurs $\vec{u}$ et $\vec{v}$ sont orthogonaux si, et seulement si, $\| \vec{u}+\vec{v} \|^2= \| \vec{u} \|^2+ \| \vec{v} \|^2$ .

Or les coordonnées de $\vec{u}+\vec{v}(X+X';Y+Y')$ .

L’égalité précédente nous donne :

$\vec{u}$ et $\vec{v}$ sont orthogonaux si, et seulement si, $\| \vec{u}+\vec{v} \|^2= \| \vec{u} \|^2+ \| \vec{v} \|^2$ .

$\vec{u}$ et $\vec{v}$ sont orthogonaux si, et seulement si,

soit

d’où

Soit

et donc les vecteurs $\vec{u}$ et $\vec{v}$ sont orthogonaux si et seulement si .

III. Définitions du produit scalaire

Définition
Soient $\vec{u}$ et $\vec{v}$ deux vecteurs de coordonnées respectives (X ; Y) et (X ‘ ; Y ‘) dans une base orthonormée.
On appelle produit scalaire de $\vec{u}$ et $\vec{v}$ , noté $\vec{u}.\vec{v}$ , le nombre réel défini par $\vec{u}.\vec{v}$ = XX’ + YY’.

IV. Cas des vecteurs colinéaires ou orthogonaux

Propriétés :

Soit $\vec{u}$ et $\vec{v}$ deux vecteurs.

Les vecteurs $\vec{u}$ et $\vec{v}$ sont orthogonaux si, et seulement si, $\vec{u}.\vec{v}$ =0.
Nous avons $\vec{u}.\vec{u}= \| \vec{u} \|^2$ .
Si les vecteurs $\vec{u}$ et $\vec{v}$ sont colinéaires de même sens , alors $\vec{u}.\vec{v}\geq\, 0$ .
Si les vecteurs $\vec{u}$ et $\vec{v}$ sont colinéaires de sens contraires, alors $\vec{u}.\vec{v}\leq\, 0$ .

V. Symétrie et bilinéarité

Propriétés :

Soient $\vec{u}$ et $\vec{v}$ des vecteurs et k un réel.
On dit que le produit scalaire est symétrique et bilinéaire.

C’est-à-dire que :

$\vec{u}.\vec{v}=\vec{v}.\vec{u}$ (symétrique)
$\vec{u}.(\vec{v}+\vec{w})=\vec{u}.\vec{v}+\vec{u}.\vec{w}$ et $(\vec{u}+\vec{v}).\vec{w}.=\vec{u}.\vec{w}+\vec{v}.\vec{w}$ (linéarité)
$(k\vec{u}) .\vec{v}=\vec{u}.(k\vec{v})=k\vec{u}.\vec{v}$

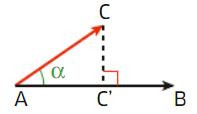
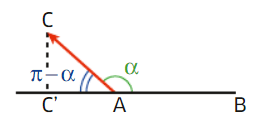
VI. Produit scalaire et angle

Propriété :

Soit A, B et C trois points.

Nous avons le produit scalaire $\vec{AB}.\vec{AC}=AB\times AC\times cos(\widehat{BAC})$ .

Télécharger puis imprimer cette fiche en PDF.

Télécharger ou imprimer cette fiche «produit scalaire : cours de maths en 1ère en PDF.» au format PDF afin de pouvoir travailler en totale autonomie.

Vous devez vous inscrire ou vous connecter à votre compte afin de pouvoir télécharger ce document au format PDF.

D'autres cours et exercices à consulter

Mathématiques Web c'est 2 268 671 fiches de cours et d'exercices téléchargées.