Corrigé des exercices sur les fonctions en 1ère.

EXERCICE 1:

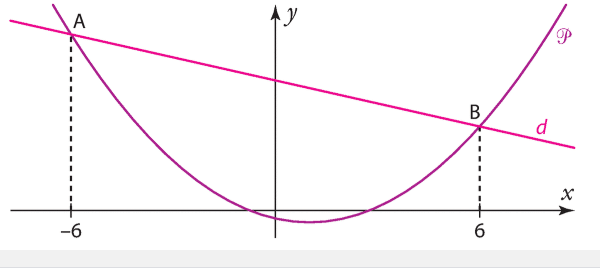
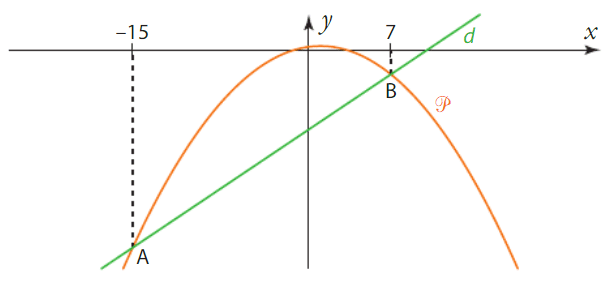
1) a) « La parabole P et la droite d se coupent en deux points, un seul point ou pas du tout. »

b) « La parabole P est située strictement au-dessus de la droite d sur l’intervalle d’intersection si les coordonnées des points d’intersection de P et d sont tous de y strictement supérieurs aux coordonnées des points d’intersection du deuxième tronçon de P et de la droite d.

La parabole P est située strictement en-dessous de la droite d sur l’intervalle d’intersection si les coordonnées des points d’intersection de P et d sont tous de y strictement inférieurs aux coordonnées des points d’intersection du deuxième tronçon de P et de la droite d. »

2) a) Les solutions de sont les abscisses des points d’intersection de la parabole P et de la droite d.

b) Les solutions de sont les abscisses des points de la parabole P situés strictement au-dessus de la droite d sur l’intervalle d’intersection.

c) Les solutions de sont les abscisses des points de la parabole P situés strictement en-dessous de la droite d sur l’intervalle d’intersection.

EXERCICE 2:

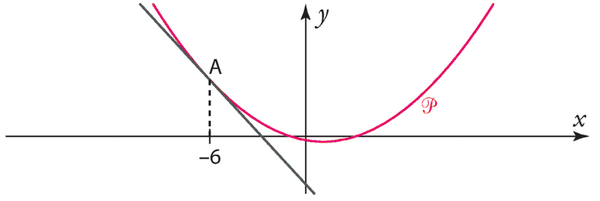
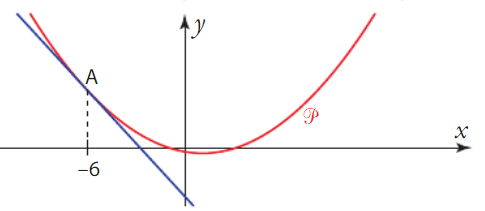
1) Pour étudier la position relative de la parabole P et de la droite d, il faut déterminer les points d’intersection de la parabole et de la droite (s’il y en a), et voir comment la parabole se positionne par rapport à la droite avant et après ces points.

2) a) Les solutions de sont les abscisses des points d’intersection de la parabole P et de la droite d.

b) Les solutions de sont les abscisses des points de la parabole P situés strictement au-dessus de la droite d sur l’intervalle d’intersection.

c) Les solutions de sont les abscisses des points de la parabole P situés strictement en-dessous de la droite d sur l’intervalle d’intersection.

EXERCICE 3:

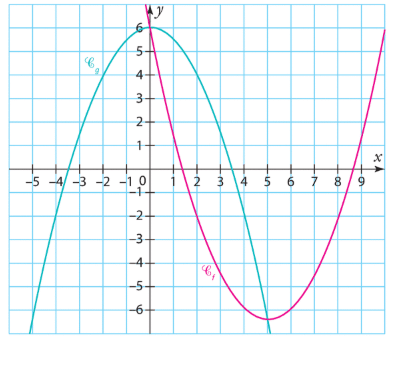
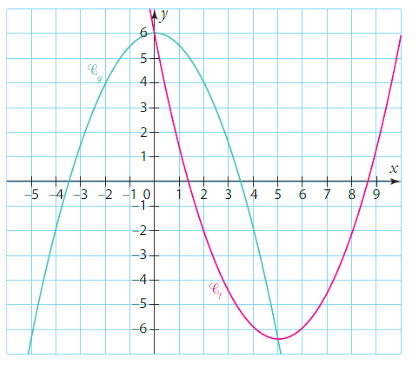
1) La position relative des courbes dépend de l’allure des courbes et de leur intersection éventuelle.

On peut voir sur le graphique que les courbes et se coupent en deux points, et que la courbe est située au-dessus de la courbe entre ces deux points.

2) a) Les solutions de sont les abscisses des points d’intersection des courbes et .

b) Les solutions de sont les abscisses des points tels que f(x) est strictement supérieur à g(x).

c) Les solutions de sont les abscisses des points tels que f(x) est strictement inférieur à g(x).

EXERCICE 4:

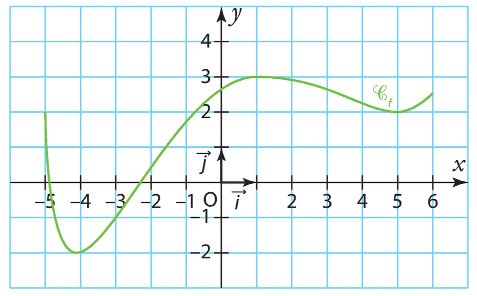
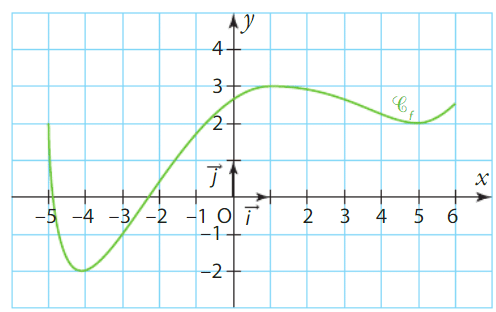
1) Les variations de f sur sont décroissantes sur , croissantes sur , puis décroissantes sur .

La fonction prend son maximum en -2 et son minimum en 3.

2) Le tableau de signes de la fonction dérivée f ‘ est :

x -5 -2 3 6

f ‘ (x) + 0 – +

EXERCICE 5:

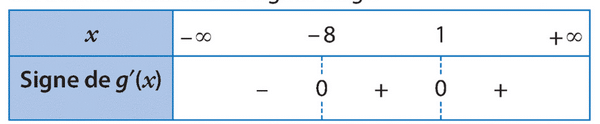
La fonction g admet un maximum local en un point où est nulle et où est strictement négative.

Dans le tableau de signes de , cela correspond à un changement de signe de + à – en 1.

Donc g admet un maximum local en , et c’est un maximum.

EXERCICE 6:

1) La fonction g admet un minimum local en un point où est nulle et où est strictement positive. Dans le tableau de signes de , cela correspond à un changement de signe de – à + en -2.

Donc g admet un minimum local en x = -2, et c’est un minimum.

2) La fonction g n’admet pas de maximum local car il n’y a pas de changement de signe de de positif à négatif.

EXERCICE 7:

1) La fonction f est de la forme , avec $a = \frac{3}{4}, b = -15$ , et c = 100.

Elle est donc de classe C² sur $\mathbb{R}$ .

Sa dérivée est $f'(x) = \frac{3}{2} x -15$ pour tout réel x.

2) Le tableau de signes de sur $\mathbb{R}$ est le suivant:

-∞ $\frac{5}{2}$ +∞
– 0 +

3) La fonction f admet un extremum local en un point où est nulle, donc en $x = \frac{5}{2}$ .

En outre, la fonction change de signe de négatif à positif en ce point, donc f admet un minimum local en $x = \frac{5}{2}$ .

EXERCICE 8:

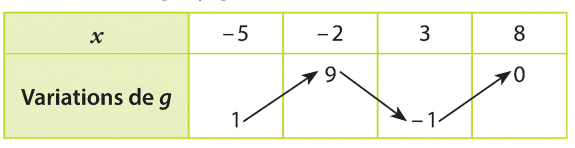
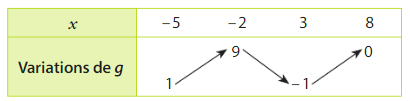
a) Pour tout x entre 3 et 8, est inférieur ou égal à 1.

b) Pour tout x entre -2 et 3, est compris entre -2 et 1.

c) Pour tout x entre -5 et 3, est compris entre -4 et 1.

d) Comme g est décroissante sur [-5;-2], est inférieur ou égal à .

e) Comme g est croissante sur [-2;3], est supérieur ou égal à .

f) Comme g est décroissante sur [-5;-2] et croissante sur [3;8], est supérieur ou égal à .

EXERCICE 9:

1. La position relative de la parabole P et de la droite d dépend de leur intersection éventuelle et de leur position relative sur les intervalles correspondants.

2. a) Les solutions de f(x) = g(x) sont les abscisses des points d’intersection de la parabole P et de la droite d.

b) Les solutions de f(x) > g(x) sont les abscisses des points de la parabole P situés strictement au-dessus de la droite d sur l’intervalle d’intersection.

c) Les solutions de f(x) < g(x) sont les abscisses des points de la parabole P situés strictement en-dessous de la droite d sur l’intervalle d’intersection.

EXERCICE 10:

1. Pour étudier la position relative de la parabole P et de la droite d, il faut déterminer leurs intersections éventuelles et voir comment la parabole se positionne par rapport à la droite avant et après ces intersections.

2. a) Les solutions de f(x) = g(x) sont les abscisses des points d’intersection de la parabole P et de la droite d.

b) Les solutions de f(x) > g(x) sont les abscisses des points de la parabole P situés strictement au-dessus de la droite d sur l’intervalle d’intersection.

c) Les solutions de f(x) < g(x) sont les abscisses des points de la parabole P situés strictement en-dessous de la droite d sur l’intervalle d’intersection.

EXERCICE 11:

1) D’après le graphique, la courbe C_f est située au-dessus de la courbe C_g sur l’intervalle [0;2] et en-dessous sur l’intervalle ]-∞;0[ et ]2;+∞[. Donc, la position relative des courbes dépend de l’intervalle considéré.

2)
a) L’équation f(x) = g(x) équivaut à l’équation f(x) – g(x) = 0, qui est également l’abscisse des points d’intersection des courbes C_f et C_g .

D’après le graphique, on peut voir qu’il y a deux points d’intersection, situés en environ -2 et 1,5.

b) L’inéquation est vraie sur l’intervalle [0;2] , où la courbe C_f est située au-dessus de C_g . Donc, les solutions de cette inéquation sont les valeurs de x appartenant à [0;2[ .

c) L’inéquation est vraie pour les valeurs de x appartenant à ]-∞;-2[ et ]2;+∞[, où la courbe C_f est située en-dessous de C_g .

Donc, les solutions de cette inéquation sont les valeurs de x appartenant à ]-∞;-2[ et ]2;+∞[.

EXERCICE 12:

1) En développant l’expression , on obtient :

2) Comme il s’agit du carré d’une expression, est toujours positif ou nul.

Donc, f(x) est toujours supérieur ou égal à g(x), pour tout x.

3) En déduire la position relative des courbes C_f et C_g : la courbe C_f est située au-dessus de la courbe C_g sur tout l’intervalle de définition commun, donc C_f est située au-dessus de C_g .

EXERCICE 13:

1) Les variations de f sur [-5;6] sont décroissantes sur [-5;3] et croissantes sur [3;6]. Le maximum est atteint en x = 3 et vaut , et le minimum est atteint en x = -5 et vaut .

2) Le tableau de signes de la fonction dérivée f’ est :

x -5 3 6
f'(x) 13 0 -3

EXERCICE 14:

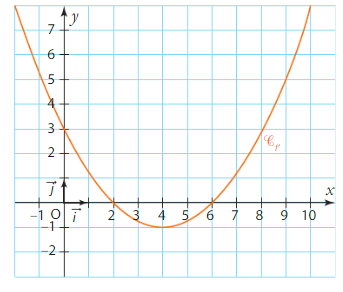
1) Sur l’intervalle [-2;10], f’ est positif sur [-2;0] et sur [4;10], et négatif sur [0;4]. Donc, le tableau de signes de est :

x -2 0 4 10
f'(x) + – – +

2) En utilisant le tableau de signes de f’, on peut dresser le tableau de variations de f :

x -2 0 4 10
f(x) déc. croiss. déc. déc.

EXERCICE 15:

D’après le tableau de signes de f’, la fonction f change de pente de positif à négatif en 2, donc f admet un maximum local en x = 2.

EXERCICE 16:

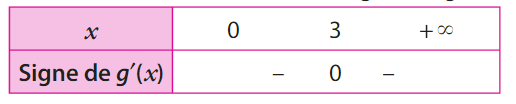
D’après le tableau de signes de g’, la fonction g change de pente de négatif à positif en 2, donc g admet un minimum local en x = 2.

EXERCICE 17:

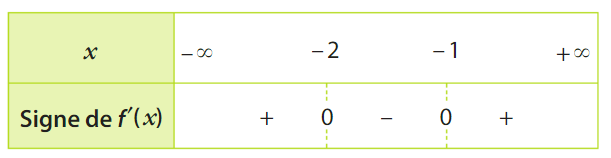
1) D’après le tableau de signes de f’, la fonction f change de pente de négatif à positif en -3, donc f admet un minimum local en x = -3.

2) D’après le tableau de signes de f’, la fonction f change de pente de positif à négatif en 1, donc f admet un maximum local en x = 1.

EXERCICE 18:

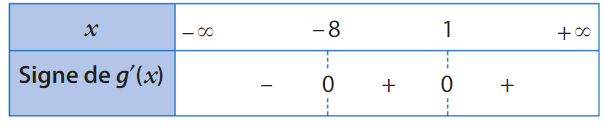
D’après le tableau de signes de g’, la fonction g ne change pas de pente, donc elle n’admet pas d’extremum local.

EXERCICE 19:

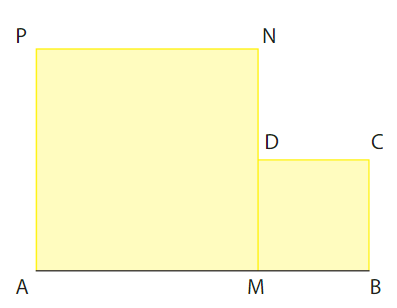
1) On a , donc $x + \frac{x}{5} + \frac{10 - x}{5}= 10$ , ce qui donne x = 2.

2) L’aire du domaine est la somme des aires des deux carrés, moins l’aire du triangle AMB. Donc :

$f(x) = 2x^2 - 10x + 100 - \frac{x(10 - x)}{2}$
$= -\frac{1 }{2}x^2 + 10x - 50$

3) La fonction f est dérivable sur son intervalle de définition, qui est , et .

4) Le maximum de f est atteint en x = 5 , où .

EXERCICE 20:

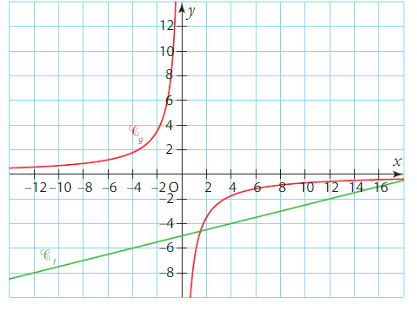
a) Pour tout réel x non nul, on a :

$f(x) - g(x) = \frac{1}{4}x^2 - 5 - \frac{-7}{x}$
= $\frac{1}{4}x^2 + \frac{7}{x} - 5$

b) Pour x > 0, le premier terme est positif, le deuxième aussi, et le troisième est négatif.

Donc est positif, ce qui implique que f(x) est supérieur à g(x) pour tout x > 0.

Pour x < 0, le premier terme est positif, le deuxième est négatif, et le troisième est négatif.

Donc est négatif, ce qui implique que f(x) est inférieur à g(x) pour tout x < 0.

Donc, f(x) est supérieur à g(x) sur ]0;+∞[ et inférieur à g(x) sur ]-∞;0[.

c) En termes de position relative des courbes C_f et C_g , la courbe C_f est donc située au-dessus de la courbe C_g sur ]0;+∞[ et en-dessous de C_g sur ]-∞;0[.

EXERCICE 21:

a) Pour tout x de [-5;8], g(x) est compris entre 17 et 33.

b) Pour tout x de [-2;3], g(x) est croissante.

c) Pour tout x de [-5;3], g(x) est décroissante.

d) Comme g est décroissante sur [-5;-2], g(b) est inférieur ou égal à g(a).

e) Comme g est croissante sur [-2;3], g(b) est supérieur ou égal à g(a).

f) Comme g est décroissante sur [-5;-2] et croissante sur [3;8], g(a) est supérieur ou égal à g(b).

Voir Corrigés 11 à 21...

Télécharger puis imprimer cette fiche en PDF.

Télécharger ou imprimer cette fiche «corrigé des exercices sur les fonctions en 1ère.» au format PDF afin de pouvoir travailler en totale autonomie.