Les fonctions et variations : cours de maths en 1ère en PDF.

Sommaire de cette fiche

Les fonctions numériques à travers un cours de maths en 1ère sur.

Cette leçon sur les fonctions et leurs variations fait intervenir les notions suivantes :

– définition d’une fonction;

– définition de l’image et de l’antécédent;

– définition de l’ensemble de définition;

– courbe représentative d’une fonction;

– sens de variation, fonction croissante, décroissante;

– tableau de variation.

Cette leçon a été rédigé par un enseignant et elle peut être télécharger gratuitement au format pdf.

I. Signe de la dérivée et sens de variation d’une fonction

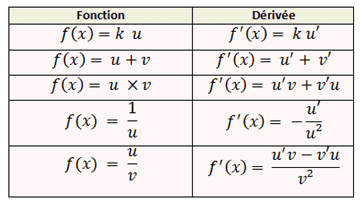
1.Rappels sur la dérivée des fonctions usuelles

2.Rappels sur les formules de dérivation

Nous admettrons sans démonstration les théorèmes suivants:

Théorème 1:

Si f est une fonction dérivable sur un intervalle [ a ; b ],
· Si, pour tout x $\in$ ] a ; b [, on a: f ‘(x) $\geq\,$ 0, alors f est croissante sur [ a ; b ].
· Si, pour tout x $\in$ ] a ; b [, on a: f ‘(x) $\leq\,$ 0, alors f est décroissante sur [ a ; b ].
· Si, pour tout x $\in$ ] a ; b [, on a: f ‘(x) = 0, alors f est constante sur [ a ; b ].

Théorème 2:

Si f est une fonction dérivable sur un intervalle I,
· Si, pour tout x $\in$ I, on a: f ‘(x) > 0 ( sauf peut-être en des points isolés où f ‘(x) = 0 ),
alors f est strictement croissante sur I.
· Si, pour tout x $\in$ I, on a: f ‘(x) < 0 ( sauf peut-être en des points isolés où f ‘(x) = 0 ),
alors f est strictement décroissante sur I.

Notons deux cas particuliers utiles:

Propriété :

Si f est une fonction dérivable sur un intervalle [ a ; b ],
· Si, pour tout x $\in$ ] a ; b [, on a f ‘(x) > 0 , alors f est strictement croissante sur [ a ; b ].
· Si, pour tout x $\in$ ] a ; b [, on a f ‘(x) < 0 , alors f est strictement décroissante sur [ a ; b ].

Exemples:

1) Soit la fonction f définie sur $\mathbb{R}$ par f(x) = x². f est dérivable sur $\mathbb{R}$ avec f ‘(x) = 2x.
· Pour tout x $\in$ ]- $\infty$ ; 0 ], on a f ‘(x) £ 0, donc f est décroissante sur ]- $\infty$ ; 0 ].
· Pour tout x $\in$ [ 0 ; + $\infty$ [, on a f ‘(x) ³ 0, donc f est croissante sur [ 0 ; + $\infty$ [.
· Pour tout x $\in$ ]- $\infty$ ; 0 [, on a f ‘(x) < 0, donc f est strictement décroissante sur ]-¥ ; 0 ].
· Pour tout x $\in$ ]0 ; + $\infty$ [, on a f ‘(x) > 0, donc f est strictement croissante sur [ 0 ; + $\infty$ [.

2) Soit la fonction f définie sur $\mathbb{R}$ par f(x) = x³. f est dérivable sur $\mathbb{R}$ avec f ‘(x) = 3x².
· Pour tout x $\in$ $\mathbb{R}$ , on a f ‘(x) ³ 0, donc f est croissante sur $\mathbb{R}$ .
· Pour tout x $\in$ ]- $\infty$ ; 0 [ È ]0 ; + $\infty$ [, on a f ‘(x) > 0, donc f est strictement croissante sur $\mathbb{R}$ .

3) Soit la fonction f définie sur $\mathbb{R}$ par f(x) = 2. f est dérivable sur $\mathbb{R}$ avec f ‘(x) = 0.
· Pour tout x $\in$ $\mathbb{R}$ , on a f ‘(x) = 0, donc f est constante sur $\mathbb{R}$ .

Nous admettrons sans démonstration les théorèmes suivants:

Théorème 3:

Si f est une fonction dérivable sur un intervalle I.
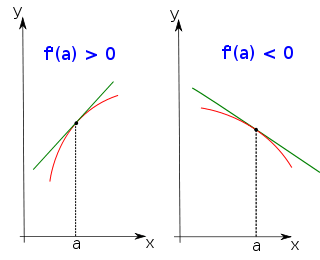
Si f admet un maximum local (ou un minimum local) en x = a différent des extrémités de l’intervalle I, alors: f ‘(a) = 0.

Théorème 4:

Si f est une fonction dérivable sur un intervalle I.
Si a $\in$ I et a différent des extrémités de I.
Si f ‘(x) s’annule pour x = a en changeant de signe.
Alors f(a) est un extremum local de f sur I.

Exemples:
1) Soit la fonction f définie sur $\mathbb{R}$ par f(x) = x². f est dérivable sur $\mathbb{R}$ avec f ‘(x) = 2x.
f ‘(x) s’annule en x = 0 en changeant de signe, donc f(0) = 0 est un extremum local de f.
Cet extremum est en réalité un minimum, car f est strictement décroissante sur ]- $\infty$ ; 0 ] et strictement croissante sur [ 0 ; + $\infty$ [. Ceci peut se résumer dans un tableau de variation.
2) Soit la fonction f définie sur $\mathbb{R}$ par f(x) = x³. f est dérivable sur $\mathbb{R}$ avec f ‘(x) = 3x².
f ‘(x) s’annule en x = 0 sans changer de signe, il n’y a donc pas d’extremum en x = 0.

5/5 - (3 votes)

Télécharger puis imprimer cette fiche en PDF.

Télécharger ou imprimer cette fiche «les fonctions et leurs variations : cours de maths en 1ère en PDF.» au format PDF afin de pouvoir travailler en totale autonomie.

D'autres cours et exercices à consulter

Mathématiques Web c'est 2 268 193 fiches de cours et d'exercices téléchargées.