Produit scalaire : exercices de maths en 1ère corrigés en PDF.

Des exercices de maths 1ère corrigés sur le produit scalaire dans le plan.

Vous retrouverez dans ces exercices sur le produit scalaire les notions suivantes :

définition du produit scalaire;
bilinéarité du produit scalaire;
symétrie du produit scalaire;
identité du parallélogramme;
produit scalaire et vecteurs orthogonaux;
équations cartésiennes et paramétriques.

Le produit scalaire dans le plan est un outil utilisé pour mesurer l’angle entre deux vecteurs. Il est défini comme le produit de la norme (ou longueur) de deux vecteurs et du cosinus de l’angle entre eux.

La bilinéarité est une propriété d’une fonction qui permet de décomposer la fonction en deux produits linéaires.

Exercice 1 :

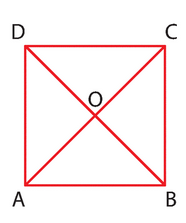
On considère le carré ABCD de centre O et de côté 8.

Calculer les produits scalaires suivants.

$a)\vec{AB}.\vec{AO}$ $b)\vec{OB}.\vec{OD}$

$c)\vec{AB}.\vec{AD}$ $d)\vec{BO}.\vec{BC}$

Exercice 2 :

On considère les vecteurs $\vec{u}$ et $\vec{v}$ tels que $\|\vec{u}\|=2$ , $\|\vec{v}\|=3$ et $\widehat{(\vec{u},,\vec{v})}=60^{\circ}$ .

Calculer leur produit scalaire.

Exercice 3 :

Déterminer une valeur en degrés de l’angle entre les vecteurs $\vec{u}$ et $\vec{v}$ tels que $\|\vec{u}\|=6$ , $\|\vec{v}\|=2$ et $\vec{u}.\vec{v},=-6$ .

Exercice 4 :

Soient les vecteurs $\vec{u},(-2;3,)$ et $\vec{v}(-1;-5)$ .

Calculer :

$a)\vec{u}.\vec{v}$ $b)(4\vec{u}).\vec{v}$ $c)(\vec{u}-\vec{v}).(\vec{u}+\vec{v})$

Exercice 5 :

On donne les points A(-3;-2) et B(1;3) et le vecteur $\vec{u}(,-5;4,)$ .

Montrer que $\vec{AB}$ et $\vec{u}$ sont orthogonaux.

Exercice 6 :

A,B,C et D étant des points quelconques du plan, montrer les égalités suivantes.

$a)\vec{AB}.\vec{CD}=\vec{BA}.\vec{DC}$ .

$b)\vec{AB}.\vec{AC}+\vec{AB}.\vec{EC}=\vec{AB}.\vec{ED}$

$c)\vec{AB}.\vec{AC}=\vec{AB}^2-\vec{BA}.\vec{BC}$

Exercice 7 :

On donne les points C et D tels que CD = 10 et H le milieu du segment [CD].

Déterminer l’ensemble des points M du plan vérifiant $\vec{MC}.\vec{MD}=-9$ .

Exercice 8 :

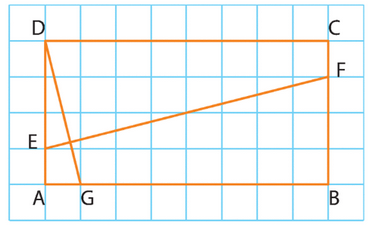
Dans un rectangle ABCD de longueur 8 et de largeur 4, on place les points E, F et G tels que :

$\vec{AE}=\frac{1}{4}\vec{AD};\vec{AG}=\frac{1}{8}\vec{AB};\vec{CF}=\frac{1}{4}\vec{CB}$ .

1. Dans le repère (A ; G,E), donner les coordonnées de tous les points de la figure.

2. Calculer le produit scalaire $\vec{EF}.\vec{DG}$ .

3. Que peut-on en déduire ?

Exercice 9 :

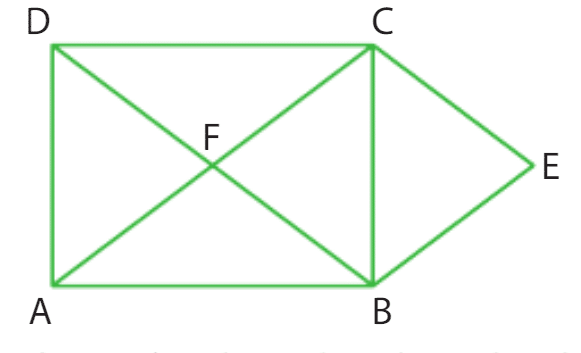
ABCD est un rectangle de centre F et E est le symétrique du point F par rapport la droite
(BC). Calculer les produits scalaires suivants.

$a)\vec{BA}.\vec{BF}\,;b)\vec{CF}.\vec{CD}\,;c)\vec{AF}.\vec{AB}\,;d)\vec{AB}.\vec{BE}$

Exercice 10 :

Soient les vecteurs $\vec{u}(2;1)$ , $\vec{v}(-3;-1)$ et $\vec{w}(1;4)$ .

Calculer les produits scalaires suivants.

$a)\vec{u}.\vec{v}\\b)\vec{w}.\vec{v}\\c)\vec{u}.(\vec{v}+\vec{w})\\d)(-2\vec{u}).\vec{v}+3(\vec{v}.\vec{w})$

Exercice 11 :

On donne les vecteurs $\vec{u}(-3;4)$ et $\vec{v}(-8;-6)$ .

Montrer que ces vecteurs sont orthogonaux.

Exercice 12 :

Donner un vecteur directeur pour chacune des droites suivantes et en déduire qu’elles sont perpendiculaires.
a) Pour les droites d1 et d2 d’équations cartésiennes 2x-3y+4=0 et 3x+2y-1= 0.
b) Pour les droites d1et d2 d’équations cartésiennes x-y+3=0 et 2x+2y-1=0.
c) Pour les droites d1 et d2 d’équations y = —3x + 1 et -x+3y-1=0.

Exercice 13 :

Soient les vecteurs $\vec{u}(-2;3)$ , $\vec{v}(-1;-5)$ .

Calculer :

$a)\vec{u}.\vec{v}\\b)(4\vec{u}).\vec{v}\\c)(\vec{u}-\vec{v}).(\vec{u}+\vec{v})$

Exercice 14 :

Soient les vecteurs $\vec{u}(-3;4)$ , $\vec{v}(-8;-6)$ .

Montrer que ces vecteurs sont orthogonaux.

2. On donne les points A(-3;-2) et B(1;3) et le vecteur $\vec{u}(-5;4)$ .

Montrer que $\vec{AB}$ et $\vec{u}$ sont orthogonaux.

Exercice 15 :

On considère les points A, B et C tels que AB = 3, AC = 4 et $\widehat{BAC}$ = 120°.

Déterminer la longueur BC.
2. On considère les points M, N et P tels que MN = 5, NP = 7 et MNP = 61°.

Déterminer la longueur MP.
3. Soit un triangle EFG tel que EF = 7, FG=6 et EG = 11.
Déterminer la valeur en degrés et arrondie à 0,1° de l’angle $\widehat{EFG}$ .
4. Soit un triangle EDF tel que EF = 5, DF = 8 et ED = 9.
Déterminer la valeur en degrés et arrondie à 0,1° de l’angle $\widehat{EDF}$ .

Exercice 16 :

soient les vecteurs $\vec{u}$ et $\vec{v}$ orthogonaux et tels que $\,\|\vec{u}\,\,\|=a$ et $\,\|\vec{v}\,\,\|=b$ .

Exprimer en fonction de a et de b les produits scalaires suivants.

$a)\vec{u}.(\vec{u}+\vec{v})\\b)(2\vec{u}-3\vec{v}).\vec{v}\\c)(\vec{u}+\vec{v})^2$

Exercice 17 :

Soit les vecteurs $\vec{u}$ ; $\vec{v}$ et $\vec{w}$ tels que : $\,\|\,\vec{u\,}\,\|=\|\vec{w\,}\,\,\|=a$ et $\vec{v}=3\vec{u}$ .

Les vecteurs $\vec{u}$ et $\vec{w}$ sont orthogonaux.

Exprimer en fonction de a les produits scalaires suivants.

$a)\vec{u}.\vec{v}\\b)\vec{v}.(\vec{u}+\vec{w})\\c)(\vec{u}+\vec{v})^2\\d)(\vec{v}+\vec{w}).(\vec{u}+\vec{w})$

Exercice 18 :

A, B, C et D étant des points quelconques du plan, montrer les égalités suivantes.
$a)\vec{AB}.\vec{CD}\,=\,BA.\vec{DC}\\b)\vec{AB}.\vec{CD}+\vec{AB}.\vec{EC}=\vec{AB}.\vec{ED}\\\,c)\vec{AB}\,.\vec{AC}=\vec{AB}\,-\vec{BA\,}-\vec{BC}$

Exercice 19 :

1.On donne les points A et B tels que AB = 12 et I le milieu du segment [AB].

Déterminer l’ensemble des points M du plan vérifiant $\vec{MA}\,.\vec{MB}\,=\,4$ .

2.On donne les points C et D tels que CD = 10 et H le milieu du segment [CD]. Déterminer l’ensemble des points M du plan vérifiant $\vec{MC}.\vec{MD\,}=\,-\,9$ .

Exercice 20 :

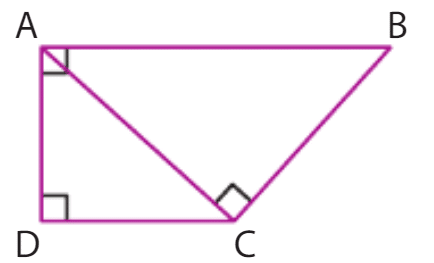
On considère un trapèze rectangle ABCD tel que la diagonale [AC] est perpendiculaire au côté [BC]. En calculant de deux manières le produit scalaire $\vec{AB}.\vec{\,AC}$ , démontrer
que $AC^2\,=\,AB\times \,CD$ .

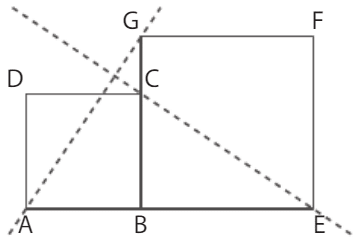
Exercice 21 :

On considère deux carrés ABCD et BEFG disposés comme sur la figure
ci-dessous tel que AB = 1 et BE = a.

A. Avec coordonnées
1. Dans le repère (A ; B, D), donner les coordonnées de tous les points de la figure.
2. Démontrer que les droites (AG) et (CE) sont perpendiculaires.

B. Sans coordonnées
1. Développer le produit scalaire $(\vec{AB}\,+\,\vec{BG}).\,(\vec{CB}\,+\,\vec{BE})$ .
2. En déduire que $\vec{AG}\,.\vec{CE}\,=\,0$ puis que les droites (AG) et (CE) sont perpendiculaires.

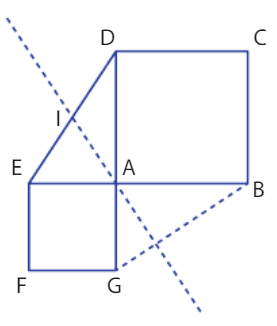
Exercice 22 :

ABCD est un carré de côté a et AEFG est un carré de côté b avec D, A et G alignés, ainsi que B, A et E comme sur la figure ci-dessous.

Le point I est le milieu du segment [DE].

A. Sans coordonnées
1. Justifier que AD + AE = 2Al.
2. Développer le produit scalaire (AD + AE) . (BA + AG).
3. En déduire que les droites (AI) et (BG) sont perpendiculaires.

B. Avec coordonnées
1. Dans le repère (A ; B, D) donner les coordonnées des points A, I, B et G.
2. En déduire que les droites (AI) et (BG) sont perpendiculaires.

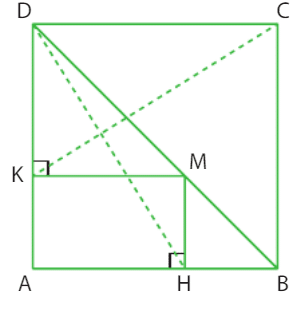
Exercice 23 :

On considère un carré ABCD de côté 1 et un point M quelconque sur le segment [BD]. On construit les projetés orthogonaux H et K du point M respectivement sur
les côtés [AB] et [AD].

1. On veut démontrer que les droites (CK) et (DH) sont perpendiculaires par deux méthodes :
a) On utilisera le repère (A ; B, D) et on notera (x;y) les coordonnées du point M.
b) On calculera le produit scalaire : $\vec{CK}.\vec{DH}$ en décomposant les vecteurs à l’aide de la relation de Chasles.
2. Démontrer que les longueurs CK et DH sont égales :
a) avec des coordonnées.
b) sans coordonnées.

3.9/5 - (25 votes)

Télécharger puis imprimer cette fiche en PDF.

Télécharger ou imprimer cette fiche «produit scalaire : exercices de maths en 1ère corrigés en PDF.» au format PDF afin de pouvoir travailler en totale autonomie.

D'autres fiches analogues :

Mathématiques Web c'est 2 243 690 fiches de cours et d'exercices téléchargées.