EXERCICE 1 :
1) Il suffit de remarquer que la droite (IJ) est incluse dans le plan (IJD) et que la droite (AC) est incluse dans le plan (ACD), donc la droite d’intersection des plans (ACD) et (IJD) est la droite (KJ). En effet, cette droite est contenue dans les deux plans et elle est non parallèle à (AC) car elle contient le point K qui est l’intersection de (AC) et (IJ).
2) Le plan P est parallèle au plan (IJD) et contient la droite (JB), donc il contient également la droite (BD) car ces deux droites sont non parallèles et situées dans le même plan. Or la droite (BD) est parallèle à (IJ) car elle est incluse dans le plan (ABC) qui est parallèle au plan (IJD) contenant (IJ). Donc D est bien parallèle à (IJ) et se trouve sur la droite D’ d’intersection de (ACD) et P.
3) Tout point de la droite D est de la forme B+t(IJ) où t est un réel. Comme D est incluse dans le plan P, tout point de D est aussi de la forme S+u(IJ)+v(BD) où u et v sont des réels. Mais BD est parallèle à (IJ) donc la droite D’ est incluse dans le plan (ACD). On en déduit que D’ est parallèle à (IJ) et donc à (DK) car K est sur la droite (IJ).
EXERCICE 2 :
1) Soit M le milieu de [IJ].
Alors , où S’ est le point d’intersection de (IJ) et (ABCD). Donc M est sur la hauteur issue de S dans le tétraèdre SIJD.
On en déduit que la droite (SM) est une hauteur de la face commune (CIJ) de ce tétraèdre et de la base ABCD. La droite (CIJ) et la droite (SM) se coupent donc en un point L qui est sur la droite (CIJ) et dans le plan de base (ABCD).
2) Le point L étant dans le plan (ABCD), il suffit de projeter la section obtenue dans ce plan sur le plan (SBC). On obtient un quadrilatère qui a pour sommets les points I, J, les intersections de la droite (IJ) avec (BC) et (CD), et le point de la droite (SM) dans le plan (SBC).
Cette section est donc un quadrilatère dont les côtés opposés sont parallèles.
1) Les plans (SAB) et (SDC) sont deux plans qui ont une droite commune (SC). Cette droite est incluse dans les deux plans, donc leur intersection est la demi-droite issue de S qui contient C.
2) Les droites (IJ) et (KL) sont toutes deux parallèles à la droite (ES) car elles sont dans le plan P qui est parallèle à (ES). Il suffit donc de montrer que les droites (IJ) et (KL) sont incluses dans le même plan pour en déduire qu’elles sont parallèles.
Or les droites (IJ) et (KL) sont toutes deux non parallèles à la droite (SC) car elles contiennent respectivement les points I et K qui ne sont pas sur (SC).
Donc la droite (IJ) et la droite (KL) sont inclues dans le plan qui contient les droites (SC) et (IL).
EXERCICE 4 :
1) Les droites (IJ) et (AD) sont toutes les deux parallèles à la droite (BC) car I, J et K sont les milieux de [SB], [SC] et [AB], donc les vecteurs SB et SC ont même direction et même sens, et le vecteur AB a même direction et même sens que le vecteur DC (car ABCD est un parallélogramme).
Ainsi, les vecteurs (IJ) et (AB) ont même direction et même sens, donc les droites (IJ) et (AD) sont parallèles.
2) Si les droites (IJ) et (AD) sont parallèles, alors le plan (SDK) (qui contient la droite (SD) et le point K) est parallèle au plan (ABCD) qui contient la droite (AD).
Mais comme (ABCD) et (SDK) ne sont pas parallèles, ils doivent se couper en une droite commune, qui est la droite (IJ).
3) La droite (SK) est incluse dans le plan (SKD), et elle coupe le plan (SBC) le long de la droite (BC), qui est incluse dans (SBC) car ABCD est un parallélogramme.
Ainsi, l’intersection des plans (SKD) et (SBC) est la droite (SK) coupée par le plan (SBC) le long de (BC). Pour construire cette intersection, on peut donc tracer la droite (SK) à partir de S et la droite (BC) à partir de B ou C (peu importe lequel), et trouver leur intersection P qui est sur la droite (SK), puis tracer la droite (SP) qui est l’intersection des deux plans recherchés.
4) Pour trouver l’intersection de la droite (IJ) avec le plan (SKD), il suffit de trouver un point de la droite (IJ) qui est dans le plan (SKD). Or, le point I est dans le plan (SKD) car la droite (IJ) est parallèle à (AD) qui est dans (SKD), donc il suffit de tracer la droite (SI) pour trouver l’intersection recherchée.
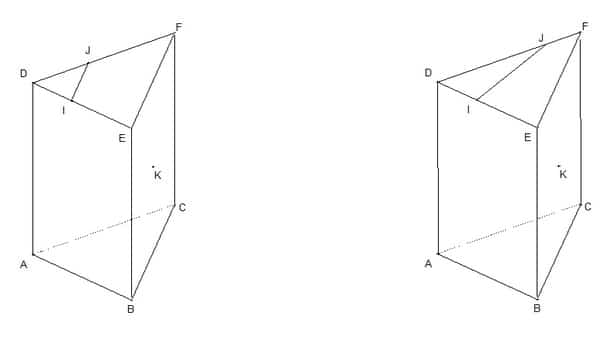
EXERCICE 5 :
1) Comme K est le centre de la face BCFE, la droite (IK) passe par K et est perpendiculaire à (BC) et (FE), donc elle est incluse dans le plan (BCF).
De même, la droite (JK) est incluse dans (BCF). Ainsi, l’intersection de (IJK) avec (BCF) est une droite qui est parallèle à la fois à (IK) et (JK), donc à (IJ).
2) Pour construire l’intersection de (IJK) avec (ABC), on peut procéder ainsi :
– On construit la droite (KL) parallèle à (BC) et passant par L. Cette droite coupe la face ABCD du prisme en un point P (car elle est incluse dans le plan (ABC) qui contient ABCD).
– On construit la droite (KM) parallèle à (AC) et passant par M. Cette droite coupe la face ABFE du prisme en un point Q (car elle est incluse dans le plan (ABFE) qui contient ABFE).
– On trace la droite (PQ), qui est incluse dans le plan (ABC) car elle est la droite d’intersection des plans (ABC) et (ABFE) (qui ont en commun la droite [AB]).
La droite (PQ) est l’intersection de (IJK) avec (ABC), car elle passe par I, J (qui sont sur (IJK)) et par P, Q (qui sont sur les plans (ABC) et (BCF) respectivement).
3) Dans ce cas, on peut procéder ainsi :
– On construit la droite (KN) qui est incluse dans le plan (BCF) et passe par K et N.
– La droite (IJ) est incluse dans le plan (DFE) qui est parallèle à (BCF), donc elle coupe (BCF) en une droite parallèle à (IJ) qu’on appellera (d).
– On trace la perpendiculaire à (d) passant par N, qui coupe (BCF) en un point L.
– On construit la droite (LK) parallèle à (BC) et passant par L. Cette droite coupe la face ABCD en un point P.
– On construit la droite (KM) parallèle à (AC) et passant par M. Cette droite coupe la face ABFE en un point Q.
– La droite (PQ) est l’intersection de (IJK) avec (ABC), comme dans le premier cas.
Il faut noter que dans ce deuxième cas, on n’a pas suffisamment d’informations pour justifier les constructions (par exemple, on n’a pas prouvé que les droites (IJ) et (KN) se croisent, ou que la droite (d) existe). Il faudrait des informations supplémentaires pour pouvoir justifier pleinement ces constructions.
Télécharger puis imprimer cette fiche en PDF.Télécharger ou imprimer cette fiche «corrigé des exercices sur la géométrie dans l’espace en 2de.» au format PDF afin de pouvoir travailler en totale autonomie.
D'autres cours et exercices à consulter
- Position relatives de droites et plans dans l’espace : cours de maths en 2de en PDF.
- Orthogonalité et équations de droites : cours de maths en 1ère en PDF.
- Théorème de Thalès : exercices de maths en 3ème corrigés en PDF.
- Produit scalaire : exercices de maths en terminale corrigés en PDF.
- Géométrie dans l’espace : cours de maths en 1ère en PDF.
- Triangle : exercices de maths en 5ème corrigés en PDF.
- Vecteurs et repères : exercices de maths en 2de corrigés en PDF.
- Géométrie dans l’espace : exercices de maths en 2de corrigés en PDF.