Nombres complexes : exercices de maths en terminale corrigés.

Mis à jour le 11 mai 2025

Les nombres complexes à travers des exercices de maths en terminale corrigés où nous aborderons les notions suivantes :

définition d’un nombre complexe;
écriture arithmétique;
écriture algébrique;
formule d’Euler;
formule de Moivre;
affixe d’un nombre complexe;
écriture exponentielle;
aspect géométrique des nombres complexes.

L’élève devra être capable d’effectuer des opérations sur les nombres complexes et déterminer sa partie arithmétique et imaginaire ainsi que, calculer son conjugué ou encore des mesures d’angles en maîtrisant les affixes et les images. Ces énoncés sont disponibles avec leur correction afin que vous puissiez augmenter vos notes en terminale.

Exercice 1 :

Donner la partie réelle et la partie imaginaire de chacun des nombres complexes suivants :

$z_1=1+2i\\z_2=3+i\\z_3=3\\z_4=6i\\z_5=\frac{-i}{2}+\frac{\sqrt{3}}{2}\\z_6=\frac{1}{3}(5+2i)$

Exercice 2 :

On considère les deux nombres complexes suivants :

$z_1=e^{i\frac{\pi}{3}}\,;\,\,z_2=e^{-i\frac{\pi}{4}}$

1. Ecrire $z_1$ et $z_2$ sous forme algébrique.

2. Déterminer les écritures sous formes algébrique, exponentielle et trigonométrique de $z_1z_2$ .

3. En déduire la valeur exacte du cosinus et sinus suivants :

$cos(\frac{\pi}{12})$ et $sin(\frac{\pi}{12})$ .

Exercice 3 :

Déterminer la forme algébrique de chacun des nombres complexes suivants :

$z_1=(1+i)+(-8+4i)\\z_2=(3+i)(5-2i)\\z_3=5i-(3+2i)\\z_4=2(5-i)+3(i-4)\\z_5=(i+2)^2-(3-5i)\\z_6=\,(\,\frac{1}{2}\,+i\frac{\sqrt{3}}{2}\,)^2\\z_7=\frac{5+i}{3+2i}$

Exercice 4 :

Dans le plan complexe, les points A,B et C ont pour affixe respectif $z_A=3+2i;z_B=-5+2i;z_C=-3i$

1.Placer les points A, B et C.

2. Déterminer les affixes des points A’ et B’ milieux respectifs des segments [BC] et [AC].

3. déterminer l’affixe du point G défini par $\vec{AG}=\frac{2}{3}\vec{AA'}$

Exercice 5 :

Dans le plan complexe A,B,C et D sont les points d’affixes :

$z_A=5+5i;z_B=3+2i;z_C=9-2i;z_D=11+i$ .

Déterminer les affixes des vecteurs $\vec{AD}$ et $\vec{BC}$ .
Déterminer un argument de $\frac{z_B-z_A}{z_D-z_A}$ .
En déduire la nature du quadrilatère ABCD.

Exercice 6 :

1.a. Résoudre dans $\mathbb{C}$ l’équation $z^2-2\sqrt{3}z+4=0$

b. Donner une forme exponentielle de chacun des solutions.

2. A et M sont les points d’affixes respectives $a=\sqrt{3}+i;m=\sqrt{3}-i$ .

a. Placer les points A et M en indiquant une méthode de construction.

b. On appelle B et C les points d’affixes respectives b=ia et c=ib.

Calculer b et c sous forme algébrique, puis placer B et C.

c. Démontrer que le triangle ABC est rectangle et isocèle.

d. Déterminer l’affixe du point D tel que ABCD soit un carré. Placer ce point D sur la figure.

Exercice 7 :

1)Déterminer la partie réelle et la partie imaginaire de chacun des nombres complexes :

$2+4i;2i;-1-3i;-4;2+\sqrt{3};-\sqrt{5}i$

2)Parmi ces complexes, lesquels sont des réels ?

Lesquels sont imaginaires purs?

Exercice 8 :

Ecrire les nombres complexes sous forme algébrique.

$z_1=2i+6-7i$

$z_2=3-(1+2i)$

$z_3=-5(3-i)$

$z_4=-4(1+2i)$

$z_5=1+i^2$

$z_6=i(3+2i)$

$z_7=3(5-i)+i(-1+5i)$

$z_8=i^3$

$z_9=i^4$

$z_{10}=(1+i)(1-i)$

$z_{11}=\frac{4+6i}{2}$

$z_{12}=\frac{2-3i}{5}$

$z_{13}=\frac{10+5i}{1-4i^2}$

Exercice 9 :

Déterminer le complexe conjugué de chacun des nombres complexes suivants :

$z_1=5+2i$

$z_2=-4$

$z_3=7i$

$z_4=-2-8i$

$z_5=3i-11$

$z_6=\frac{4-6i}{2}$

Exercice 10 :

Résoudre dans $\mathbb{C}$ les équations proposées.

On donnera les solutions sous forme algébrique.

$1)z-2+4i=0$

$2)5z+2i=4z-5+i$

$3)iz+1-i=0$

$4)-2z+3=iz+1-i$

$5)(2z-4+i)(z+3i)=0$

$6)(2z-4)(iz+2)=0$

$7)z^2=-16$

$8)z^2=-81$

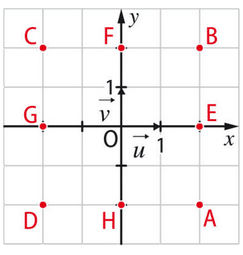
Exercice 11 :

Associer chaque complexe au point image qui lui correspond.

$z_1=2+2i$

$z_2=-2-2i$

$z_3=2$

$z_4=2i$

$z_5=-2$

$z_6=-2+2i$

Exercice 12 :

Associer chaque vecteur à l’affixe qui lui correspond.

$z_1=2+2i$

$z_2=-2+2i$

$z_3=3i$

$z_4=3-i$

$z_5=-2$

$z_6=1-i$

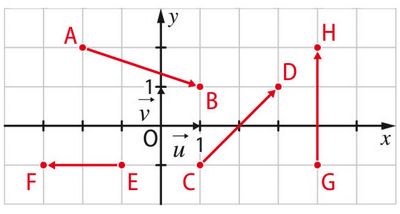
Exercice 13 :

1)Déterminer graphiquement les distances OA, OB, OC, OD, OE et OF.

2)En déduire le module de l’affixe de chacun des points A, B, C, D, E et F.

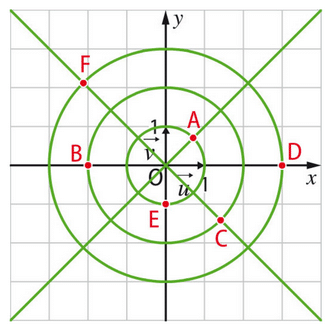
Exercice 14 :

Parmi les écritures proposées ci-dessous, dire lesquelles sont des formes trigonométriques

d’un nombre complexe.

$z_1=\sqrt{3}(cos\frac{\pi}{3}+isin\frac{\pi}{3})$

$z_2=-3(cos\frac{\pi}{4}+isin\frac{\pi}{4})$

$z_3=2(cos(\frac{5\pi}{6})+isin(-\frac{5\pi}{6}))$

$z_4=5(cos0+isin0)$

Exercice 15 :

Soit le nombre complexe $z_1$ de module 2 et d’argument $\frac{2\pi}{3}$ et le nombre complexe $z_2$

de module 4 et d’argument $-\frac{\pi}{6}$ .

1)Déterminer $|\,z_1z_2\,|$ , $|\,\frac{z_1\,}{z_2}\,|$ et $|\,z_1^5\,|$ .

2)Déterminer $arg(z_1z_2)$ , $arg(\frac{z_1}{z_2})$ et $arg(z_1^5)$ .

Exercice 16 :

Ecrire sous forme trigonométrique les nombres complexes :

$z_1=e^{i\pi}$ ; $z_2=e^{-i\frac{\pi}{2}}$ ; $z_3=e^{i\frac{2\pi}{3}}$ ; $z_4=e^{-i\frac{5\pi}{6}}$ .

Exercice 17 :

Démontrer que les nombres complexes suivants sont égaux :

$z=5i;z'=\frac{10+5i}{1-2i}$

1. En calculant la différence z’-z.

2. En calculant le quotient $\frac{z'}{z}$ .

Exercice 18 :

Ecrire sous forme algébrique le nombre complexe suivant :

$z=\frac{3+6i}{3-4i}$

Exercice 19 :

On donne $z_1=-1+3i;z_2=4-i$ .

Ecrire sous forme algébrique les nombres complexes suivants :

$a)\,z_1^2-2z_2\\b)\,z_1z_2^2\\c)\,\frac{z_1}{z_2}\\d)\,\frac{z_1}{z_2}\\,e)\,\frac{1}{z_1}+\frac{1}{z_2}\\f)\,,\frac{1}{z_1^2}+\frac{1}{z_2^2}$

Exercice 20 :

Calculer la somme $S=1+i+i^2+i^3+....+i^{2017}$ .

Exercice 21 :

On pose $j=-\frac{1}{2}+i\frac{\sqrt{3}}{2}$ .

Calculer $j^2,j^3$ puis $j^n$ suivant les valeurs du nombre entier naturel n.
Vérifier que $1+j+j^2=0$ .
Calculer la somme $S'=1+j+j^2+j^3+......j^{2017}+j^{2018}$ .

Exercice 22 :

P est le polynôme défini sur $\mathbb{C}$ par $P(z)=z^2-4z+5$ .

Vérifier que $P(2+i)=0\,et\,P(2-i)=0$ .

Exercice 23 :

Le plan complexe est rapporté à un repère orthonormé direct d’unité graphique 2 cm.

On considère les points A,B,C et H d’affixes respectives : $a=-3-i;b=-2+4i;c=3-i;h=-2$ .

1.a) Placer ces points sur une figure, qui sera complétée au fur et à mesure de l’exercice.

b) Montrer que V est le centre du cercle $\xi$ circonscrit au triangle ABC. Préciser le rayon du cercle $\xi$ .

c) Calculer, sous forme algébrique, le nombre complexe $\frac{b-c}{h-a}$ .

En déduire que les droites (AH) et (BC) sont perpendiculaires.

2. Dans la suite de cet exercice, on admet que H est l’orthocentre du triangle ABC, c’est-à-dire le point d’intersection des hauteurs du triangle ABC.

a. On note G le centre de gravité du triangle ABC.

L’affixe du point G vérifie $g=\frac{1}{3}(a+b+c)$ .

Placer le point G sur la figure.

b) Montrer que le centre de gravité G, l’orthocentre H et le centre du cercle circonscrit au triangle ABC, noté V, sont alignés. Le vérifier sur la figure.

c) On note A’ le milieu de [BC] et K celui de [AH]. Déterminer la nature du quadrilatère KHA’V.

Remarque : dans un triangle, le centre de gravité, l’orthocentre et le centre du cercle circonscrit au triangle sont alignés sur une droite (d) appelée droite d’Euler.

Exercice 24 :

On considère le plan complexe P rapporté à un repère orthonormé $(O\,;\vec{u},\vec{v})$ , et on considère
les points A, B et C distincts situés sur le cercle de centre O et de rayon r.
Les points A’, B’ et C’ sont les images de A, B et C par la rotation de centre O et d’angle $\frac{\pi}{3}$ .
Les points U, V et W sont les milieux des segments [A’B], [B’C], [C’A] ; montrer que le triangle UVW est équilatéral.

Exercice 25 :

Le plan complexe est rapporté à un repère orthonormé $(O\,;\vec{u},\vec{v})$ , et on considère l’application
f du plan complexe dans lui-même qui au point M d’affixe z associe le point M’ d’affixe $f(z)=\frac{z+i\overline{z}}{2}$ .

1. Montrer que l’ensemble (d) des points M dont l’affixe z vérifie f(z) = z est une droite.
2. Montrer que le nombre $\frac{f(z)-z}{1-i}$ est réel.
3. En déduire que M’ appartient à la droite ∆ passant par M et de vecteur directeur $\vec{u}-\vec{v}$
4. Montrer que pour tout nombre complexe z, $f(f(z))=f(z)$ .
5. Déduire des questions précédentes que M’ est le point d’intersection des deux droites (d) et
∆.
6. Caractériser géométriquement l’application f.

Exercice 26 :

On considère le plan complexe rapporté à un repère orthonormé $(O\,;\vec{u},\vec{v})$ .
On désigne par A le point d’affixe 1 et par C le cercle de centre A et de rayon 1.

PARTIE A :
Soit F le point d’affixe 2, B le point d’affixe $z_B=1+e^{i\frac{\pi}{3}}$ et E le point d’affixe $z_E=1+z_B^2$ .

Montrer que le point B appartient au cercle C.
Déterminer une mesure en radians de l’angle $\,(\,\vec{AF},\vec{AB}\,\,)$ . Placer le point B.
Déterminer la forme exponentielle des nombres complexes $z_B-z_A$ et $z_E-z_A$ .
En déduire que les points A, B et E sont alignés. Placer le point E.

PARTIE B :
Pour tout nombre complexe z tel que $z\neq\,1$ , on considère les points M et M’ d’affixes respectives z et z’ où $z'=1+z^2$ .
Pour $z\neq\,0$ et $z\neq\,1$ , donner, à l’aide des points A, M et M’ une interprétation géométrique d’un argument du nombre complexe $\frac{z'-1}{z-1}$ .
En déduire que les points A, M et M’ sont alignés si et seulement si $\frac{z^2}{z-1}$ est un réel.

Exercice 27 :

On considère le plan complexe rapporté à un repère orthonormé $(O\,;\vec{u},\vec{v})$ , et l’application
f du plan complexe dans lui-même qui au point M d’affixe z associe le point M’ d’affixe $z^3-3z^2+3z$ .
On considère les points B et C d’affixe respectives i et $i\sqrt{3}$ .

1. Calculer les affixes des points images de O, B et C par f.
2. Placer les points B et C et leur image B’ et C’ .
3. L’application f conserve-t-elle l’alignement ?
4. Montrer qu’un point M d’affixe z est invariant par f si et seulement si z vérifie l’équation :
$z^3-3z^2+3z=0$ .

5. En déduire que f possède trois points invariants dont on déterminera les affixes.
6. Montrer pour tout z de $\mathbb{C}$ , $z'-1=(z-1)^3$ .

Exercice 28 :

On considère le plan complexe P rapporté à un repère orthonormé $(O\,;\vec{u},\vec{v})$ .
On considère le point M d’affixe z, le point $M_1$ d’affixe z , le point A d’affixe 2 et le point B d’affixe 1. Soit f l’application de P privé de A dans P, qui à tout point M d’affixe z associe le point M’ d’affixe z’ tel que $z'=\frac{z+4}{\overline{z}-2}$ .
Déterminer les points invariants par f .

Télécharger puis imprimer cette fiche en PDF.

Télécharger ou imprimer cette fiche «nombre complexes : exercices de maths en terminale corrigés en PDF.» au format PDF afin de pouvoir travailler en totale autonomie.

Nos applications

Mathématiques Web c'est 2 269 513 fiches de cours et d'exercices téléchargées.

Continuez votre apprentissage

Cours de terminale

Exercices de terminale