Corrigé des exercices sur la dérivée d’une fonction en 1ère.

EXERCICE 1 :

a) La fonction f est définie sur l’ensemble des nombres réels, donc elle est dérivable sur $\mathbb{R}$ .

Sa dérivée est .

b) La fonction g est définie sur l’ensemble des nombres réels non nuls, donc elle est dérivable sur $\mathbb{R}^*$ . Sa dérivée est $g'(x) = -\frac{1}{x^2}$ .

c) La fonction h est définie sur l’intervalle $[0;+\infty[$ , donc elle est dérivable sur cet intervalle.

Sa dérivée est $h'(x) = \frac{3}{2}\sqrt{x}$ .

d) La fonction j est définie sur $\mathbb{R} - \{-\frac{2}{9} \}$ , donc elle est dérivable sur cet ensemble. Sa dérivée est $j'(x) = \frac{25}{(9x+2)^2}$ .

EXERCICE 2 :

La fonction g est définie sur l’ensemble des nombres réels, donc elle est dérivable sur $\mathbb{R}$ .

Sa dérivée est $g'(x) = 5(-9x+1)^4 \times (-9)$ .

Simplifiée, on obtient .

EXERCICE 3 :

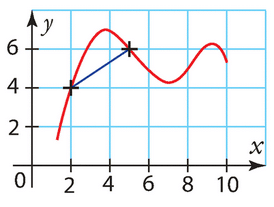
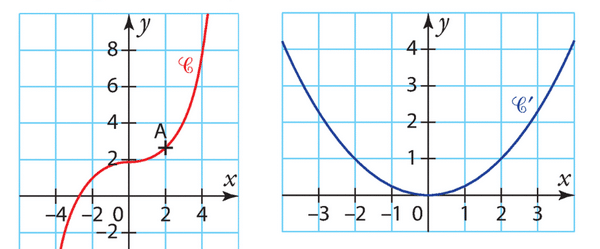
Le taux de variation de f entre 2 et 5 est donné par la formule $TV = \frac{f(5) - f(2)}{5 - 2}$ .

D’après le graphique, on a et.

Donc, le taux de variation de f entre 2 et 5 est $TV = \frac{7-1}{5-2} = 2$ .

EXERCICE 4 :

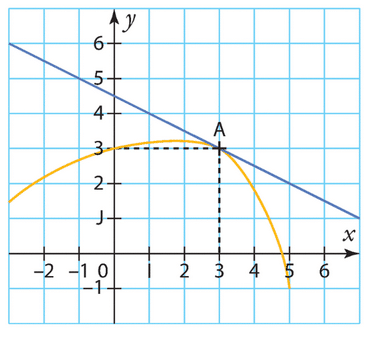
La droite passant par et a pour coefficient directeur $m = \frac{6-1}{1-(-2)} = \frac{5}{3}$ . Comme la droite est tangente à la courbe en A, on a $f'(-2) = m = \frac{5}{3}$ .

EXERCICE 5 :

1. On a $f(x) - f(9) = \sqrt{x}-3 - (\sqrt{9}-3) = \sqrt{x} - 6$ et $f(9+h) - f(9) = \sqrt{9+h} - 3 - (\sqrt{9}-3) = \sqrt{9+h} - 6$ .

En utilisant l’identité remarquable , on peut écrire :

$f(9+h) - f(9) = (\sqrt{9+h} + 3)(\sqrt{9+h}-3) = 9 + h - 9 = h$

Le taux de variation de f entre 9 et est donc $TV = \frac{f(9+h) - f(9)}{h} = \frac{1}{\sqrt{9+h} + 3}$ .

2. Comme la limite de cette expression quand h tend vers 0 est finie, la fonction f est dérivable en 9 et sa dérivée est $f'(9) = \frac{1}{\sqrt{9} + 3} = \frac{1}{6}$ .

EXERCICE 6 :

On a g(3) = 6 (coordonnée y du point B).

Comme la tangente en A a pour coefficient directeur $-\frac{1}{g'(3)}$ , on peut écrire : $-\frac{1}{g'(3)} = \frac{6-1}{3-(-2)} = \frac{5}{5} = 1$ .

Donc, g'(3) = -1.

EXERCICE 7 :

a) On peut écrire $f(x) = \frac{1}{x} + x = u(x) + v(x)$ avec $u(x) = \frac{1}{x}$ et .

Les fonctions u et v sont dérivables sur $\mathbb{R}^*$ et sur $\mathbb{R}$ , respectivement.

La fonction somme est dérivable sur $\mathbb{R}^* \ {-0}$ et sa dérivée est $(u+v)'(x) = u'(x) + v'(x) = -\frac{1}{x^2} + 1$ .

b) On peut écrire $g(x) = -5 + \frac{1}{x^2} = u(x) + v(x)$ avec et $v(x) = \frac{1}{x^2}$ .

Les fonctions u et v sont dérivables sur $\mathbb{R}$ et sur $\mathbb{R}^*$ , respectivement.

La fonction somme est dérivable sur $\mathbb{R}^*$ et sa dérivée est $(u+v)'(x) = u'(x) + v'(x) = 0 - \frac{2}{x^3} = -\frac{2}{x^3}$ .

c) On peut écrire avec et .

Les fonctions u et v sont dérivables sur $\mathbb{R}$ et la fonction somme est dérivable sur $\mathbb{R}$ avec .

EXERCICE 8 :

1. L’équation de la courbe représentative de f est « $y=-\frac{9}{2x^2-4x+3}$ ».

2. Nous plaçons un point sur la courbe en .

3. Nous traçons la tangente à la courbe en ce point.

4. Le coefficient directeur de la tangente est environ 11.

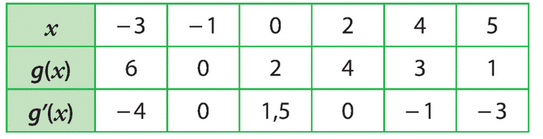
5. En plaçant le point sur les différentes valeurs de x données dans le tableau de valeurs et en traçant les tangentes, on peut estimer les valeurs approchées des dérivées demandées : $f'(-2) \approx 11, f'(-1) \approx -7, f'(0) \approx 5, f'(1) \approx -2, f'(2)\approx -7$ .

EXERCICE 9 :

1. Les points sont .

2. En chacun de ces points, on trace la tangente à la courbe .

3. Une allure possible de est représentée ci-dessous :

Courbe à créer….

EXERCICE 10 :

Le coefficient directeur de la tangente à 6 (c’est-à-dire au point d’abscisse 2) est la valeur de la dérivée f'(2). En lisant sur le graphique, on a $f'(2) \approx -2$ . Donc le coefficient directeur de la tangente à 6 est environ -2.

EXERCICE 11 :

a) La fonction f est définie pour tout x sauf 0. Donc, f est dérivable sur $\mathbb{R}^*$ et sa dérivée est $f'(x) = -\frac{5}{2x^2} - \frac{7}{2}x$ .

b) La fonction g est définie pour tout x sauf 0. Donc, g est dérivable sur $\mathbb{R}^*$ et sa dérivée est $g'(x) = \frac{44}{5x^2} - \frac{4}{5}$ .

c) La fonction h est définie pour tout x sauf 3. Donc, h est dérivable sur $\mathbb{R} - \{3\}$ et sa dérivée est $h'(x) = \frac{18x^2 - 41x + 8}{(7x - 21)^2}$ .

d) La fonction j est définie pour tout x sauf 0. Donc, j est dérivable sur $\mathbb{R}^*$ et sa dérivée est $j'(x) = -\frac{10}{(3x^2+2)^2}$ .

e) La fonction k est définie sur l’intervalle ]-∞;1[ ∪ ]1;+∞[ car le dénominateur s’annule en x = 1 .

On peut factoriser en , donc la fonction est dérivable sur cet intervalle. Sa dérivée est $k'(x) = \frac{9(5 - 2x)}{(x - 1)^3 (x - 5)}$ .

f) La fonction m est définie pour tout x tel que , c’est-à-dire sur $]-\infty ; 10]$ .

Donc, m est dérivable sur cet intervalle et sa dérivée est $m'(x) = -\frac{1}{2\sqrt{10-x}}$ .

EXERCICE 12 :

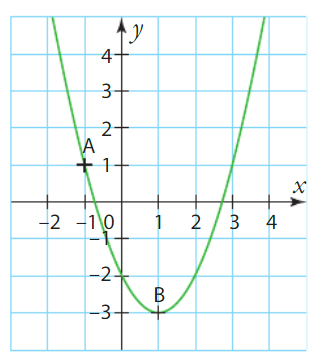
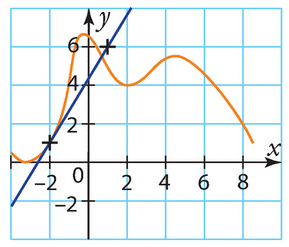
Le taux de variation de f entre -1 et 1 est donné par la formule $TV = \frac{f(1) - f(-1)}{1 - (-1)}$ .

D’après le graphique, on a f(-1) ≈ -6 et $f(1) \approx 2$ .

Donc, le taux de variation de f entre -1 et 1 est $TV \approx \frac{2-(-6)}{2} = 4$ .

EXERCICE 13 :

On peut écrire l’égalité sous la forme : $\frac{f(-7+h)-f(-7)}{h} - \frac{15}{3}h = 4h$ .

En simplifiant, on obtient : $\frac{f(-7+h)-f(-7)}{h} = 4h + 5h$ .

Donc, le taux de variation de f entre et -7+h est TV = 9.

Comme ce taux ne dépend pas de h, on peut dire que la fonction f est dérivable en -7 et que .

EXERCICE 14 :

En faisant tendre x vers 3 dans l’équation $\frac{g(x) - g(3)}{x-3} = 2x+3$ , on trouve ,

donc $g'(3) = \frac{3}{2}$ .

Donc la fonction g est dérivable en 3 et $g'(3) = \frac{3}{2}$ .

EXERCICE 15 :

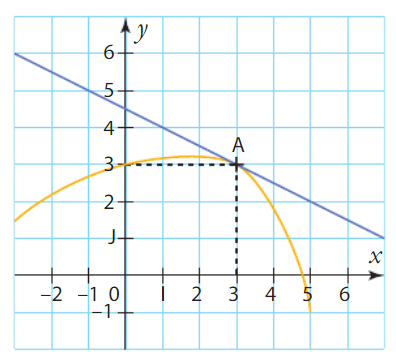
On a g(3) = 6 (coordonnée y du point B).

Comme la tangente en A a pour coefficient directeur $-\frac{1}{g'(3)}$ , on peut écrire : $-\frac{1}{g'(3)} = \frac{6-(-13)}{3-(-3)} = \frac{19}{6}$ .

Donc, $g'(3) = -\frac{6}{19}$ .

EXERCICE 16 :

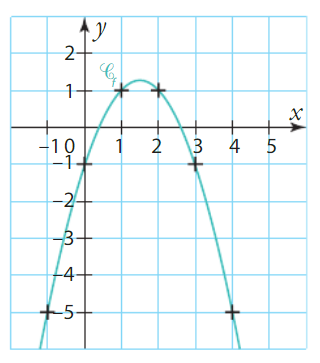
La courbe représentative C_f est reproduite ci-dessous :

Tracer la courbe….

La tangente en 2 a pour équation $y = f'(2)(x-2) + f(2) \approx -x + 5$ , et la tangente en 0 a pour équation .

EXERCICE 17 :

Pour les fonctions simples :
– La fonction f est dérivable sur $\mathbb{R}$ , et sa fonction dérivée est f'(x) = 4x^3.
– La fonction g est dérivable sur $\mathbb{R}$ , et sa fonction dérivée est g'(x) = 12x^11.
– La fonction h est dérivable sur $\mathbb{R}^{*}$ (l’ensemble des nombres réels non nuls), et sa fonction dérivée est $h'(x) = -\frac{1}{x^{2}}$ .

Pour les fonctions composées :
– Pour f, on peut identifier $u(x) = \frac{1}{x}$ et .

Les fonctions u et v sont toutes deux dérivables sur R*, et donc la fonction somme f est dérivable sur R*, et sa fonction dérivée est f'(x) = -1/x^2 + 1.
– Pour g, on peut identifier u(x) = -5 et $v(x) = \frac{1}{x^2}$ .

Les fonctions u et v sont toutes deux dérivables sur R* (avec une exception en x=0 pour v), et donc la fonction somme g est dérivable sur R* (avec une exception en x=0), et sa fonction dérivée est $g'(x) = \frac{2}{x^3}$ .
– Pour h, on peut identifier et .

Les fonctions u et v sont dérivables sur R, et donc la fonction somme h est dérivable sur R, et sa fonction dérivée est .

EXERCICE 18 :

Pour les fonctions composées :
– Pour f, on peut identifier $u(x) = \frac{1}{x}$ et . La fonction u est dérivable sur R* (avec une exception en x=0), et la fonction v est dérivable sur R, donc la fonction produit f est dérivable sur R* (avec une exception en x=0), et sa fonction dérivée est $f'(x) = -\frac{9}{x^2} + 6$ .
– Pour g, on peut identifier et $v(x) = \sqrt {x}$ .

Les fonctions u et v sont dérivables sur $[0,+\infty[$ , donc la fonction produit g est dérivable sur $[0,+\infty[$ , et sa fonction dérivée est $g'(x) = 3x^{\frac{3}{2}}$ .
– Pour h, on peut identifier et .

Les fonctions u et v sont dérivables sur R, donc la fonction produit h est dérivable sur R, et sa fonction dérivée est .

EXERCICE 19 :

1. On peut écrire $f(x) = (2x+8)^{-1}$ . On résout l’équation , ce qui donne x = -4 . Donc v(x) s’annule en .

2. Le théorème de la dérivée de l’inverse d’une fonction affirme que si f est une fonction dérivable sur un intervalle I et à valeurs dans un intervalle J, alors si g est l’inverse de f, c’est-à-dire une fonction qui vérifie pour tout x de J, alors g est dérivable sur J et sa dérivée est donnée par la formule : $g'(x)= \frac{1}{f'(g(x))}$ .
Ici, la fonction f est dérivable sur I et à valeurs dans $]0,+\infty[$ , donc elle est bijective sur son ensemble de définition et admet une inverse.

On peut déterminer cette inverse en résolvant l’équation en x :

on a équivaut à $(2x+8)^{-1} = y$ , soit $2x+8 = y^{-1}$ , soit $x = \frac{y^{-1}-8}{2}$ .

Donc l’inverse de f est la fonction $g : y \mapsto \,\frac{y^{-1}-8}{2}$ .

La dérivée de g en y est donnée par $g'(y) = \frac{1}{f'(g(y))}$ , donc $g'(y) = \frac{1}{-2(y^{-1}-8)^2}$ .

On peut donc exprimer f'(x) en fonction de x en utilisant la formule $g'(f(x)) =\frac{ 1}{f'(x)}$ :

on a $f'(x) =\frac{ 1}{g'(f(x))} = -2(2x+8)^2$ .

Donc f est dérivable sur I et sa dérivée est .

EXERCICE 20 :

1. On peut écrire où $g(x) = \sqrt{x}$ et . Donc g est définie sur $[0,+\infty[$ et f est dérivable sur I, donc h est définie et dérivable sur I.

2. En utilisant la formule de la dérivée d’une fonction composée, on a $h'(x) = g'(f(x)) \times f'(x)$ où $g'(x) = \frac{1}{2\sqrt{x}}$ et .

Donc $h'(x) = -\frac{3}{2\sqrt{-3x+12}}$ .

3. On a et $g'(x) = \frac{1}{2\sqrt{x}}$ pour tout x strictement positif.

4. On a donc $h'(x) = -\frac{3}{2\sqrt {-3x+12} }$ .

EXERCICE 21 :

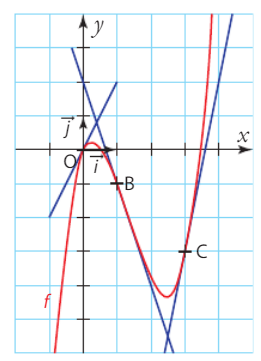
1. Graphiquement, on lit les pentes des tangentes en 0, 1 et 3 sur le graphe de f : la pente en 0 est nulle, la pente en 1 est négative et la pente en 3 est positive.

2. La tangente en C a pour coefficient directeur la dérivée en 3, soit f'(3) = 7. On utilise ensuite l’équation de la tangente en C : .

On a et donc l’équation réduite de la tangente en C est .

3. On calcule f'(x) en dérivant f(x) terme à terme : .

On trouve et .

On peut vérifier que ces valeurs correspondent bien aux pentes des tangentes trouvées graphiquement. On peut également retrouver l’équation de la tangente en C en utilisant cette dérivée : et , donc l’équation réduite de la tangente en C est , soit .

Voir Corrigés 11 à 21...

Télécharger puis imprimer cette fiche en PDF.

Télécharger ou imprimer cette fiche «corrigé des exercices sur la dérivée d’une fonction en 1ère.» au format PDF afin de pouvoir travailler en totale autonomie.