Corrigé des exercices sur les suites numériques en 1ère.

EXERCICE 1 :

On a :

$u_0=2\times 0+3=3$
$u_1=2\times 1+3=5$
$u_2=2\times 2+3=7$

Donc et .

EXERCICE 2 :

On a :

$u_0=\frac{0+1}{2\times 0-3}=-\frac{1}{3}$
$u_{10}=\frac{10+1}{2\times 10-3}=\frac{11}{17}$

Donc $u_0=-\frac{1}{3}$ et $u_{10}=\frac{11}{17}$ .

EXERCICE 3 :

On a :

$u_{n+1}=2(n+1)-1=2n+1+2=2n+3=u_n+2$
$u_{n-1}=2(n-1)-1=2n-3=u_n-4$
$u_{2n}=2\times 2n-1=4n-1=2(2n)-1=u_{n+1}$
$u_{n+1}=2(n+1)-1=2n+3=u_n+2$

Donc $u_{n+1}=u_n+2, u_{n-1}=u_n-4, u_{2n}=u_{n+1}$ et $u_{n+1}=u_n+2$ .

EXERCICE 4 :

1) On a :

$u_1=\frac{2\times 2-2}{2-3}=2$
$u_2=\frac{2\times 2-2}{2-3}=2$

Donc et .

2) En calculant les termes suivants, on trouve :

$u_3=-\frac{2}{5} \\\\ u_4=-6 \\\\ u_5=\frac{2}{5} \\\\ u_6=-\frac{2}{5} \\\\ u_7=\frac{2}{5} \\\\ u_8=-\frac{2}{5} \\\\ u_9=\frac{2}{5} \\\\ u_{10}=-\frac{2}{5} \\\\ u_{11}=2$

Donc $u_{15}=-\frac{2}{5}$ à $10^{-2}$ près.

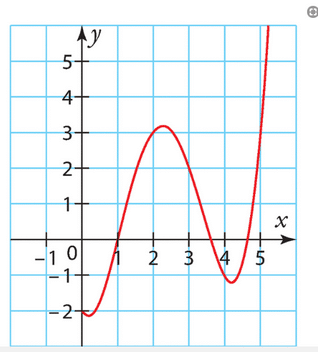
EXERCICE 5 :

En lisant graphiquement les valeurs de f, on a :

$u_0=1 \\\\ u_1=4 \\\\ u_2=3 \\\\ u_3=0 \\\\ u_4=-5$

Donc et .

EXERCICE 6 :

1) On a :

Donc .

2) On a :

$u_{20}=-3+2\times 20=37$

Donc $u_{20}=37$ .

EXERCICE 7 :

a) On a :

$u_{n+1}=u_n-4=u_{n-1}-8$

Donc la suite est arithmétique de raison -4.

b) On a :

$v_{n+1}=-(n+1)+3=-n+2=-v_n+5$

Donc la suite est arithmétique de raison 5.

c) On a :

$w_{n+1}=(n+1)^2-3=n^2+2n+1-3=w_n+2n+1$

Donc la suite n’est pas arithmétique.

EXERCICE 8 :

a) On a :

$u_{n+1}=\frac{u_n}{2}=\frac{u_{n-1}}{2^2}=\dots=\frac{u_0}{2^{n+1}}=\frac{2}{2^{n+1}}=\frac{1}{2^n}$

Donc la suite est géométrique de raison $\frac{1}{2}$ .

b) On a :

$v_{n+1}=-3^{n+1}=(-3)^n\times (-3)=-v_n\times 3$

Donc la suite est géométrique de raison .

c) On a :

$w_{n+1}=\frac{1}{4^{n+1}}=\frac{1}{4^n\times 4}=\frac{1}{4^n}\times \frac{1}{4}=\frac{1}{4^n}\times \frac{1}{4^n}\times \frac{1}{4}=\frac{w_n}{4}$

Donc la suite est géométrique de raison $\frac{1}{4}$ .

EXERCICE 9 :

1) On a :

(tout le gâteau est dans l’assiette)
$u_1=\frac{1}{2}$ (après le premier service, il reste la moitié)
$u_2=\frac{1}{2}\times \frac{1}{2}=\frac{1}{4}$ (après le deuxième service, il ne reste plus que le quart)

Donc et $u_1= \frac{1}{2}$ .

2) En se servant à chaque fois de la moitié de ce qui reste, Yacine divise par 2 la proportion de gâteau qui reste dans l’assiette, c’est-à-dire que la raison de la suite est $\frac{1}{2}$ .

EXERCICE 10 :

a) On a :

$u_{n+1}-u_n=(n+1)^2+2(n+1)-n^2-2n-4n-8=2n+3>0$

Donc la suite est strictement croissante.

b) On a :

$u_{n+1}-u_n=\frac{4}{n+2}-\frac{4}{n+1}=\frac{4n+4}{(n+2)(n+1)}<0$

Donc la suite est strictement décroissante.

c) On a :

$u_{n+1}-u_n=-5^{n+1}+5^n=-4\times 5^n<0$

Donc la suite est strictement décroissante.

EXERCICE 11 :

1) On a :

$\frac{u_{n+1}}{u_n}=\frac{2^{n+1}}{n+1}\times \frac{n}{2^n}=\frac{2}{1+\frac{1}{n}}\longrightarrow 2$

Donc la suite (U_n) est géométrique de raison 2.

2) On a :

$\frac{2n}{n+1}>1\quad \Leftrightarrow \quad 2n>n+1\quad \Leftrightarrow \quad n>1$

Donc l’inéquation est vérifiée pour tout entier n plus grand que 1.

3) La raison de la suite (u_n) est strictement positive, donc cette suite est strictement croissante.

EXERCICE 12 :

1) On a :

$u_n=1,5(u_{n-1})=1,5^2(u_{n-2})=\dots=1,5^n$

Donc .

2) On a :

$u_{10}=1,5^{10}=576,75$

Donc la 10ème poupée mesure 576,75 cm (ou 5,7675 m).

3) Si on empile les poupées, leur hauteur est égale à la somme de leur taille, c’est-à-dire :

$- 1+1,5+1,5^2+\dots+1,5^9 \approx 29,1499$

Donc la pile de 10 poupées a une hauteur d’environ 29,1499 cm.

EXERCICE 13 :

1) On a :

$u_0=2\times 0 +3=3 \\\\ u_1=2\times 1 +3=5 \\\\ u_2=2\times 2 +3=7$

Donc u_0=3, u_1=5 et u_2=7.

2) On a :

$u_0=\frac{0+1}{2\times 0-3}=-\frac{1}{3} \\\\ u_{10}=\frac{10+1}{2\times 10-3}=\frac{11}{17}$

Donc $u_0=-\frac{1}{3}$ et $u_{10}=\frac{11}{17}$ .

3) On a :

$u_0=2^0-1=0 \\\\ u_1=2^1-1=1 \\\\ u_2=2^2-1=3 \\\\ u_3=2^3-1=7 \\\\ u_4=2^4-1=15$

Donc et u_4=15 .

4) On a :

$u_{n+1}=2(n+1)-1=2n+1+2=2n+3=u_n+2 \\\\ u_{n-1}=2(n-1)-1=2n-3=u_n-4 \\\\u_{2n}=2^{2n}-1=(2^n)^2-1=(2^n-1)(2^n+1)=u_n(u_n+2) \\\\ u_{n+1}=2(n+1)-1=2n+3=u_n+2$

Donc $u_{n+1}=u_n+2, u_{n-1}=u_n-4, u_{2n}=u_n(u_n+2)$ et $u_{n+1}=u_n+2$ .

5) On a :

$u_{n+1}=(n+1)^2+1 \\\\u_{n-1}=(n-1)^2+1 \\\\u_{2n}=4n^2+1 \\\\ u_{n+1}=n^2+2n+1+1=(n+1)^2$

Donc $u_{n+1}=(n+1)^2+1, u_{n-1}=(n-1)^2+1, u_{2n}=4n^2+1$ et $u_{n+1}=(n+1)^2+1$ .

EXERCICE 14 :

1) On a :

$u_1=\frac{1}{2}\times 200+80=180 \\\\u_2=\frac{1}{2}\times 180+80=140$

Donc u_1=180 et u_2=140.

2) On a :

$u_{n+1}=\frac{1}{2}\times u_n+80$

Donc la suite (u_n) est une suite arithmético-géométrique, mais il n’y a pas de forme explicite pour ses termes.

EXERCICE 15 :

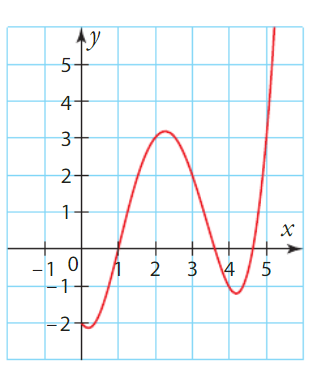
En lisant graphiquement les valeurs de f, on a :

$\\\\u_0=1 \\\\u_1=2 \\\\ u_2=5 \\\\u_3=10 \\\\ u_4=17$

Donc et u_4=17 .

EXERCICE 16 :

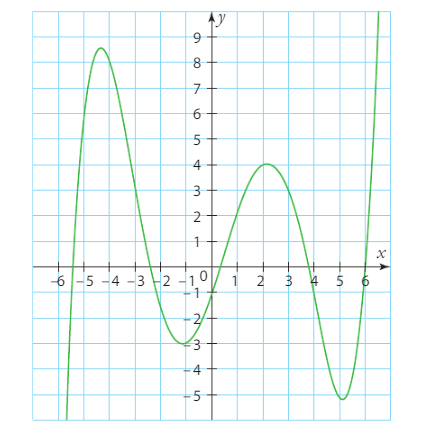
En lisant graphiquement les valeurs de f, on a :

$v_0=1 \\\\ v_1=4 \\\\ v_2=17 \\\\ v_3=58 \\\\v_4=175$

Donc et v_4=175 .

EXERCICE 17 :

1) On a :

Donc et u_3=14 .

2) On a :

Donc .

EXERCICE 18 :

a) On a :

$u_{n+1}-u_n=2n+2>0$

Donc la suite (u_n) est strictement croissante.

b) On a :

$u_{n+1}-u_n=\frac{4}{n+2}-\frac{4}{n+1}=-\frac{4}{(n+2)(n+1)}<0$

Donc la suite (u_n) est strictement décroissante.

c) On a :

$u_{n+1}-u_n=-5^{n+1}+5^n=-4\times 5^n<0$

Donc la suite (u_n) est strictement décroissante.

EXERCICE 19 :

1) On a :

$\frac{u_{n+1}}{u_n}=\frac{2^{n+1}}{n+1}\times \frac{n}{2^n}=\frac{2}{1+\frac{1}{n}}\longrightarrow 2$

Donc la suite (U_n) est géométrique de raison 2.

2) On a :

$\frac{2n}{n+1}>1\quad \Leftrightarrow \quad 2n>n+1\quad \Leftrightarrow \quad n>1$

Donc l’inéquation est vérifiée pour tout entier n plus grand que 1.

3) La raison de la suite (u_n) est strictement positive, donc cette suite est strictement croissante.

EXERCICE 20 :

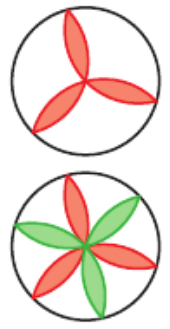
1) La rosace à l’étape 2 ressemble à ça :

Donc u_1=6 .

2) On a :

u_1=6

Donc u_1=6 et u_2=9 .

3) On peut remarquer que pour passer de l’étape n à l’étape n+1, on ajoute 4 pétales (un entre chaque paire de pétales déjà existants), donc la relation entre u_n et $u_{n+1}$ est :

$u_{n+1}=u_n+4$

Donc la suite (u_n) est arithmétique de raison 4.

4) On peut conjecturer que la limite de la suite est l’infini, car à chaque étape, le nombre de pétales est multiplié par environ 4/3.

5) On a :

$v_0=0,1\times 1=0,1$
$v_1=0,1\times 5=0,5$

Donc v_0=0,1 et v_1=0,5 .

6) On peut remarquer que pour passer de l’étape n à l’étape n+1, on multiplie l’épaisseur par 2 (car on plie en deux chaque couche), donc la relation entre v_n et $v_{n+1}$ est :

$v_{n+1}=2v_n$

Donc la suite (v_n) est géométrique de raison 2.

7) Comme la raison de la suite (v_n) est strictement positive, cette suite est strictement croissante.

8) On a :

$v_n=0,1\times 2^n$

Donc $v_n=0,1\times 2^n$ .

9) On peut résoudre l’équation $0,1\times 2^n=324$ pour trouver la valeur de n, soit environ n=10,04 étapes (il faut donc 11 étapes).

Voir Corrigés 11 à 20...

Télécharger puis imprimer cette fiche en PDF.

Télécharger ou imprimer cette fiche «corrigé des exercices sur les suites numériques en 1ère.» au format PDF afin de pouvoir travailler en totale autonomie.