les fonctions et limites : exercices de maths en terminale corrigés.

Les fonctions numériques et le calcul de limite avec des exercices de maths en terminale corrigés afin de réviser et pouvoir s’entraîner. Vous pouvez aussi les télécharger gratuitement au format PDF.

Cette fiche fait intervenir les notions suivantes :

taux d’accroissement:
limites;
dérivée et formules de dérivation;
continuité;
théorème de point fixe;
asymptotes à la courbe représentative d’une fonction.

L’élève devra être capable d’étudier entièrement une fonction domaine de définition, dérivée, équations de tangente, asymptotes et sens de variation) mais également savoir déterminer une limite en un point ou en l’infini après avoir levé une forme indéterminée. Ces fiches sur les fonctions et le calcul d’une limite disposent de leur correction en terminale.

Exercice 1 :

g est la fonction définie sur l’intervalle $]0;+\infty[$ par $g(x)=\frac{1}{x}+1$ .

Démontrer que, pour tout nombre réel $\alpha >0$ , l’intervalle $]1-\alpha ;1+\alpha [$ contient toutes les valeurs g(x) pour x assez grand.
En déduire la limite de la fonction g en $+\infty$ .
Interpréter graphiquement cette limite.

Exercice 2 :

h est la fonction définie sur l’intervalle $]1;+\infty[$ par $h(x)=\frac{1}{x^2-1}$ .

1.Démontrer que, pour tout nombre réel $\alpha >0$ , l’intervalle $]-\alpha ;+\alpha [$ contient toutes les valeurs

h(x) pour x assez grand.

2.En déduire la limite de la fonction h en $+\infty$ .

3.Interpréter graphiquement cette limite.

Exercice 3 :

f est la fonction définie sur $\mathbb{R}$ par .

Etudier la limite de f en $+\infty$ .

2. g est une fonction définie sur l’intervalle $]-1;+\infty[$ par $g(x)=\frac{4x^2-x+5}{x+1}$ .

Etudier la limite de la fonction g.

a) en $+\infty$ b) en – 1.

Exercice 4 :

g est la fonction définie sur $\mathbb{R}$ par $g(x)=\frac{e^x+1}{e^x-1}$

Etudier la limite de la fonction g en $-\infty$ .
a) Démontrer que, pour tout nombre réel x, $g(x)=\frac{1-e^{-x}}{1+e^{-x}}$ .

b) Etudier la limite de la fonction g en $+\infty$ .

Exercice 5 :

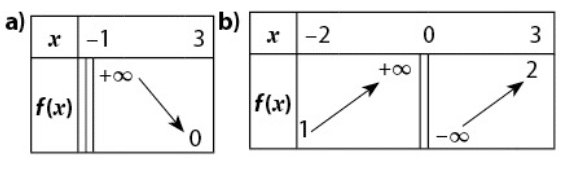
Dans chacun des cas, on donne le tableau de variation d’une fonction f.

Tracer, à main levée, une courbe $\varphi$ susceptible de représenter la fonction f dans un repère.

Exercice 6 :

Donner, sans justification, la limite des fonctions suivantes en $+\infty$ .

$a)\,f(x)=x\sqrt{x}\\b)\,g(x)=(x^2+1)(-x^2+2)\\c)\,h(x)=e^x ( \frac{1}{x} +2 )\\d)\,k(x)=x^2 ( -3- \frac{1}{x} )$

Exercice 7 :

Une usine fabrique une puce destinée aux appareils électroniques.

Le coût total de fabrication est modélisé par la fonction C définie sur l’intervalle $[0;+\infty[$

par $C(q)=\frac{8}{1+e^{-q}}$ où q désigne la quantité de puces fabriquées (en milliers)

et C(q) le coût total (en millions d’euros).

a. Représenter graphiquement la fonction C à l’écran de votre calculatrice.

b. Etudier la limite de la fonction C en $+\infty$ .

2. On note le coût moyen de fabrication d’une puce lorsqu’on en fabrique q (avec q>0).

a. Exprimer en fonction de q.

b. Représenter graphiquement la fonction à l’écran de la calculatrice.

c. Etudier la limite de la fonction en $+\infty$ .

Interpréter le résultat obtenu en termes économiques.

Exercice 8 :

g est la fonction définie sur $\mathbb{R}$ par :
.
Louise a affiché la courbe représentative de g à l’écran de sa calculatrice.
Elle conjecture : « La fonction g a pour limite $+\infty$ en $+\infty$ . »
a) k désigne un nombre entier naturel.
Calculer $g(k\pi)$ .
b) Expliquer alors pourquoi Louise se trompe.

Exercice 9 :

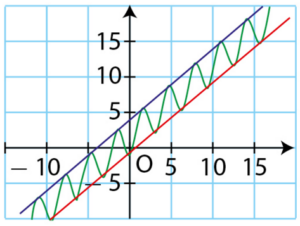
Voici dans un repère orthonormé la courbe représentative de la fonction f:
$x \mapsto x-1 +5 sin^2 (x)$
et les droites d’équations
y = x— 1 et y=x+ 4.
Étudier les limites de la fonction f en $-\infty$ et en $+\infty$ .

Exercice 10 :

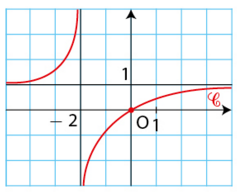
Voici la courbe représentative $\varphi$ d’une fonction f définie sur $]- \infty, -2[ \cup ]- 2; + \infty,[$ .
1. Lire sur le graphique, les limites de la fonction f en $-\infty$ , en $+\infty$ , à droite et à gauche en – 2.
2. g est la fonction définie pour x différent de – 2 et de 0 par $g(x) = \frac{1}{f(x)}$ .
Déterminer Ia limite de la fonction g en :
a) $-\infty$ b) $+\infty$ c) d) à droite et à gauche en O.
3. h est la fonction définie sur $]- \infty, -2[ \cup ]0; + \infty,[$ par $h(x)=\sqrt{f(x)}$ .

Déterminer la limite de la fonction h en :
a) $-\infty$ b) $+\infty$ c) d) O.

Exercice 11 :

g est la fonction définie sur $[0 ; +\infty[$ par :
$g(x)=\frac{2x-1}{\sqrt{x^2+1}}$
a) Montrer que pour tout x > 0,
$g(x)=\frac{2-\frac{1}{x}}{\sqrt{1+\frac{1}{x^2}}}$
b) Déterminer l’équation de l’asymptote à la courbe représentative de g dans un repère orthonormé.

Exercice 12 :

g est la fonction définie sur $\mathbb{R}$ par :
$g (x) = e^{-x} sin(x).$
On note $\varphi$ la courbe représentative de la fonction g dans un repère orthonormé.
a) Utiliser un encadrement de g(x) pour étudier la limite de g en $+\infty$ .
b) En déduire une asymptote d à la courbe $\varphi$ .
c) Montrer que la courbe $\varphi$ coupe une infinité de fois son asymptote d.
2. Numa affirme : « La limite de la fonction g en $-\infty$ est $+\infty$ ».

Expliquer pourquoi Numa se trompe.

Exercice 13 :

1. h est la fonction définie $[0 ; +\infty[$ par :
$h(x)=\frac{e^{2x}}{x+e^x}$
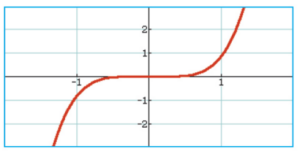
Voici la courbe représentative de la fonction h à l’écran d’une calculatrice.

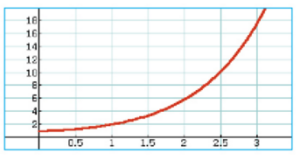
a) Conjecturer la limite de la fonction h en $+\infty$ .
b) Démontrer cette conjecture.
Conseil : mettre en facteur au dénominateur.
2. k est la fonction définie sur $]-\infty ; -1]$ par $k(x)=\frac{e^{2x}}{x+e^x}$
a) Afficher la courbe représentative de k à l’écran de la calculatrice et conjecturer la limite de k en $-\infty$ .
b) Prouver cette conjecture.

Exercice 14 :

Pour tout réel a, on note la fonction définie sur $\mathbb{R}$ par $h_a(x)=\frac{ax+\frac{1}{2}}{e^x}$
1 . a) Déterminer la limite de la fonction en $+\infty$ .
b) Suivant les valeurs du nombre réel a, déterminer la limite de la fonction en $-\infty$ .
2. a) Démontrer que pour tout réel x :
$h_a'(x)=\frac{-ax+a-\frac{1}{2}}{e^x}$
b) Démontrer que pour tout réel $a\neq 0$ , la fonction admet un extremum pour une valeur de x que l’on exprimera en fonction de .
3. Dans un repère orthonormé, on note $\varphi _a$ la courbe représentative de la fonction .
Voici les courbes pour cinq valeurs de a :

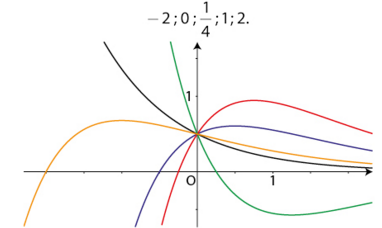
Déterminer, pour chacune des courbes tracées, la valeur de a correspondante, en justifiant les réponses.

Exercice 15 :

Pour tout réel non nul $\lambda$ , on désigne par $f_\lambda$ la fonction définie sur R par :
$f_\lambda(x)=\frac{e^{\lambda x}+e^{-\lambda x}}{2\lambda}$

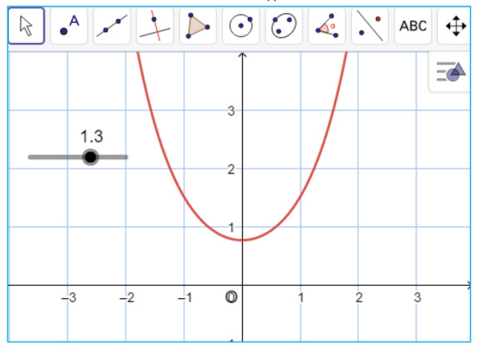
1.a) Tracer, à l’aide d’un logiciel de géométrie, la courbe représentative de la fonction $f_\lambda$ .

b) Conjecturer, suivant les valeurs de $\lambda$ , les limites de la fonction $f_\lambda$ en $-\infty$ et en $+\infty$ .
2. Démontrer les conjectures précédentes.

5/5 - (4 votes)

Télécharger puis imprimer cette fiche en PDF.

Télécharger ou imprimer cette fiche «fonctions et limites : exercices de maths en terminale corrigés en PDF.» au format PDF afin de pouvoir travailler en totale autonomie.

D'autres cours et exercices à consulter

Mathématiques Web c'est 2 268 028 fiches de cours et d'exercices téléchargées.