Fonction convexe : cours de maths en terminale en PDF.

Sommaire de cette fiche

La fonction convexes ou concaves à travers un cours de maths en terminale est un chapitre essentiel à bien assimiler par l’élève.

I. Convexité d’une fonction

1.Sécante à la courbe représentative d’une fonction.

Définition :

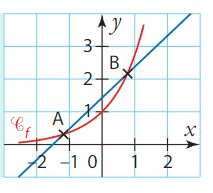
Soit f une fonction et C_f sa courbe représentative dans un repère.
Soit A et B deux points de C_f alors la droite (AB) est sécante de C_f .

2.Convexité et concavité.

Définitions :

Soit f une fonction et C_f sa courbe représentative dans un repère orthonormé du plan.

On dit que :

f est convexe sur un intervalle I si, pour tout réel x de I, est en dessous de ses sécantes.
f est concave sur un intervalle I si, pour tout réel x de I, est au-dessus de ses sécantes.

3. les fonctions usuelles.

Propriété :

La fonction $x \mapsto \sqrt{x}$ est concave.

Les fonctions $x \mapsto x^2$ et $x \mapsto e^x$ sont convexes.
La fonction $x \mapsto \frac{1}{x}$ est convexe sur $\mathbb{R}$ .

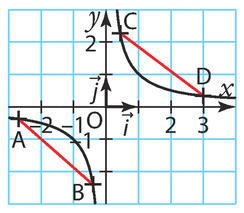
Exemple :
Soit f la fonction inverse définie sur $\mathbb{R}^*$ par $f(x)=\frac{1}{x}$ et sa courbe représentative
dans le repère ci-dessous.

Alors le segment [CD] est au-dessus de la courbe de pour x strictement positif donc f est
convexe sur $\mathbb{R}^{+*}$ et le segment [AB] est en dessous de la courbe pour x strictement négatif
donc f est concave sur $\mathbb{R}^{-*}$ .

4.Position par rapport aux sécantes.

Propriété :

• Si f est une fonction convexe sur un intervalle I alors pour tous réels x et y de I et pour tout $t\in[0;1]$ , on a :
$f(tx+ (1 - t)y) \leq\, tf(x)+ (1 - t)f(y)$
• Si f est une fonction concave sur un intervalle I alors pour tous réels x et y de I et pour tout t $t\in[0;1]$ , on a :
$f(tx+ (1 - t)y) \geq\, tf(x)+ (1 - t)f(y)$

Démonstration :
Soient deux réels x et y et soit $t\in[0;1]$ .

Soit et ; Alors le point
appartient au segment [AB], sécante de .

f étant convexe, cette sécante est située au-dessus de .
M est donc situé au-dessus du .
D’où $f(tx+(1-t)y)\leq\, tf(x)+(1-t)f(y)$ .

Remarque :

Si les inégalités précédentes sont strictes, on dira que f est une fonction strictement convexe ou strictement concave sur l.

Propriété : concavité.

est convexe sur I si et seulement si - f est concave.

Exemple :

Soit fla fonction définie sur $\mathbb{R}$ par .

La fonction $x \mapsto e^x$ est convexe, donc $f:x \mapsto -e^x$ est concave.

II. Fonction convexe et dérivées première et seconde

1.Fonction convexe et fonction concave.

Théorème :

Soit I un intervalle réel.
Soit f une fonction deux fois dérivable sur I et sa fonction dérivée.

f est convexe sur l, si et seulement si, pour tout réel x de l, est croissante.
f est concave sur l, si et seulement si, pour tout réel x de l, est décroissante.

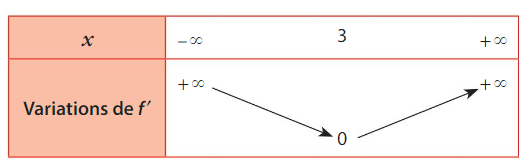
Exemple :
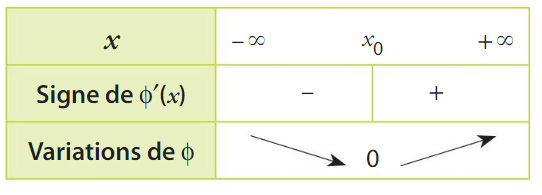
Soit f la fonction définie et dérivable sur $\mathbb{R}$ .
On a dressé le tableau de variations de la fonction .

Alors f est concave sur $]-\infty ; 3]$ et convexe sur $[3;+\infty [$ .

2.La fonction dérivée seconde.

Définition :

Soit f une fonction supposée deux fois dérivable sur I et sa fonction dérivée.
On appelle dérivée seconde de la fonction f, notée f'' , la dérivée de .

Exemple :
Soit f la fonction définie (et dérivable deux fois) sur $\mathbb{R}$ par l’expression
Alors et .

Remarques :

La dérivée seconde d’une fonction affine est toujours nulle.
La fonction exponentielle est égale à sa dérivée, donc à sa dérivée seconde également.

3.Convexité et dérivée seconde.

Théorème :

Soit f une fonction supposée deux fois dérivable et sa fonction dérivée.

f est convexe sur I si et seulement si, pour tout réel x de l, est positive.
f est concave sur I si et seulement si, pour tout réel x de l, est négative.

Démonstration :

f’ est croissante (resp. décroissante) si et seulement si est est positive (resp. négative).
Donc f est convexe (resp. concave) si et seulement si est positive (resp. négative).

III. Tangente et point d’inflexion

1.Dérivée seconde et tangente.

Propriété :

Soit f une fonction supposée deux fois dérivable sur I de dérivée seconde f'' .

Si f'' est positive sur I, alors la courbe représentative de f est au-dessus de ses tangentes.

Preuve :

Soit $\phi$ la fonction définie sur I par la différence entre la fonction et sa tangente.
$\phi(x)=f(x)-(f'(x_0)(x-x_0)+f(x_0))=f(x)-f'(x_0)x+f'(x_0)x_0-f(x_0)$ .
Alors $\phi$ est dérivable comme somme de fonctions dérivables et, en notant $\phi'$ sa dérivée, on obtient :

$\phi'(x)=f'(x)-f'(x_0)+0-0=f'(x)-f'(x_0)$ .

Or est positive donc est croissante. D’où :
si $x\geq\, x_0$ alors $f'(x)\geq\, f'(x_0)$ donc $\phi'(x)\geq\, 0$ .
si $x\leq\, x_0$ alors $f'(x)\leq\, f'(x_0)$ donc $\phi'(x)\leq\, 0$ .
De plus, $\phi(x_0) = f(x_0)-f'(x_0)x_0 + f'(x_0)x_0 -f(x_0)=0$

On obtient le tableau de variations ci-dessous.

Donc, pour tout réel x de I, $\phi(x)\geq\, 0$ donc $f(x)\geq\, f'(x_0)(x-x_0)+f(x_0)$ autrement dit, la courbe représentative de f est au-dessus de ses tangentes.

Conclusion :

Si est positive, alors la courbe représentative de f est au-dessus de ses tangentes.

Remarques :

Si est négative sur I alors la courbe représentative de f est en dessous de ses tangentes.
Attention à la réciproque, une fonction convexe n’est pas obligatoirement deux fois dérivable.

2.Point d’inflexion à la courbe représentative d’une fonction.

Définition :

Soit f une fonction deux fois dérivable sur un intervalle I et C_f sa courbe représentative sur cet intervalle
dans un repère orthonormé du plan.
Soit A un point de C_f et T_A la tangente C_f au point A.
On dit que A est un point d’inflexion pour C_f si, au point A, la courbe C_f traverse T_A .

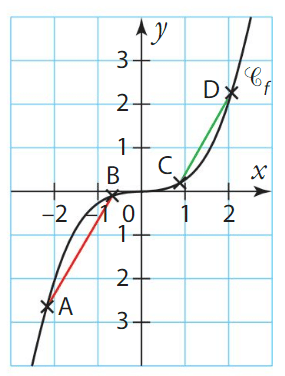
Exemple :
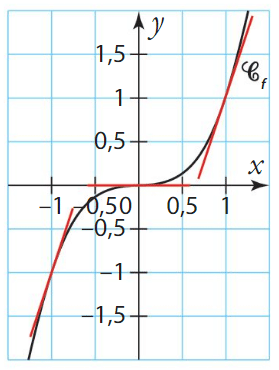
Soit f la fonction cube et sa courbe représentative dans un repère.

Alors l’origine du repère est un point d’inflexion pour .

En revanche les tangentes en -1 et en 1 ne traversent pas la courbe, les points de coordonnées et ne sont donc pas des points d’inflexion.

Propriété :

Pour qu’il y ait point d’inflexion, il faut que f'' change de signe donc que change de variation.

Exemple :

Si alors et .
Donc $f''(x)\geq\, 0\Leftrightarrow x\geq\, 0$ et $f''(x)\leq\, 0\Leftrightarrow x\leq\, 0$ .

Il y a changement de signe de la dérivée seconde, donc f change de convexité, il y a donc en un point d’inflexion.

4.5/5 - (4 votes)

Télécharger puis imprimer cette fiche en PDF.

Télécharger ou imprimer cette fiche «fonctions convexe ou concave : cours de maths en terminale en PDF.» au format PDF afin de pouvoir travailler en totale autonomie.

D'autres cours et exercices à consulter

Mathématiques Web c'est 2 268 052 fiches de cours et d'exercices téléchargées.