Corrigé des exercices sur les équations en 2de.

EXERCICE 1 :

1) Pour résoudre cette équation, on développe le produit des quatre expressions entre parenthèses :

Ce produit est nul si et seulement si l’une des expressions entre parenthèses est nulle. Donc, on résout les équations :

– 2x – 2 = 0 ⇔ x = -1
– 3x – 3 = 0 ⇔ x = 1
– 0.04x – 0.4 = 0 ⇔ x = 10

Les solutions de l’équation () sont donc et .

2) On cherche à déterminer les solutions de l’équation :

$\frac{2x + 3}{5x - 1} = 2$

On commence par multiplier chaque membre de l’équation par pour éliminer le dénominateur :

On développe et on réduit :

$x = \frac{7}{18}$

La solution de l’équation (E2) est donc $x = \frac{7}{18}$ .

3) On cherche à résoudre l’équation :

On regroupe les termes en x et on réduit :

$x = \frac{2,8}{5,6}$

x = 0,5

La solution de l’équation (E3) est donc .

4) On cherche à résoudre l’équation :

$\frac{3}{x} = \frac{x}{5}$

On multiplie chaque membre de l’équation par x pour éliminer le dénominateur :

$3 = \frac{x^2}{5}$

On multiplie chaque membre de l’équation par 5 :

On obtient une équation du second degré qu’on résout :

$x = \pm\sqrt{15}$

Les solutions de l’équation (E4) sont donc $x = -\sqrt{15}$ et $x = \sqrt{15}$ .

5) On cherche à résoudre l’équation :

$(x - 2)^2 = \frac{1}{16}(5 - 2x)^2$

On développe les deux membres de l’équation et on réduit :

On obtient une équation du second degré qu’on résout :

Les solutions de l’équation (E5) sont donc x = 1 et x = 8.

6) On cherche à résoudre l’équation :

$\frac{x-4}{x-2} = \frac{x+2}{x}$

On élimine les dénominateurs en multipliant chaque membre de l’équation par x(x – 2) :

On développe et on réduit :

On réduit encore :

On factorise par x :

On résout l’équation du second degré :

Les solutions de l’équation (E6) sont donc x = 1, x = 8 et x = 0.

7) On développe les deux membres de l’équation :

On réduit et on obtient une équation du second degré :

On divise les deux membres de l’équation par 3 pour simplifier :

On résout cette équation du second degré en utilisant la formule générale :

$x_1 = -1, x_2 = \frac{1}{2}$

Les solutions de l’équation (E7) sont donc x = -1 et x = 1/2.

8) On cherche à résoudre l’équation :

$\frac{x^2}{1 - 2x} = -1$

Comme le membre de gauche est négatif, il n’existe pas de solution réelle à cette équation.

9) On développe et on réduit les deux membres de l’équation :

On réduit et on obtient une équation du second degré :

On résout cette équation du second degré en utilisant la formule générale :

Les solutions de l’équation () sont donc x = -2 et x = 6.

10) On multiplie chaque membre de l’équation par 2x – 3 pour éliminer le dénominateur :

On développe et on réduit :

On résout cette équation du second degré en utilisant la formule générale :

La solution de l’équation $(E_{10})$ est donc x = 2.

EXERCICE 2:

a) En développant et simplifiant, on obtient :

$\frac{x}{2} - \frac{3}{2} = \frac{2x}{6} + \frac{5}{6}$
$-\frac{x}{2} - \frac{2x}{6} = \frac{5}{6} + \frac{3}{2}$

$-\frac{5x}{6} = \frac{17}{6}$

$x = -\frac{17}{5}$

Donc l’équation admet une solution unique $x = -\frac{17}{5}$ .

b) En développant et simplifiant l’équation, on obtient :

$x^2 + 2x - 3 = 0\\\\ (x-1)^2 - 1 - 3 = 0\\\\ (x-1)^2 = 4\\\\ x-1 = \pm2$

Donc l’équation admet deux solutions et .

c) En développant et simplifiant l’équation, on obtient :

Donc l’équation admet deux solutions $x_1 = \frac{4}{3}$ et $x_2 = -\frac{1}{3}$ .

d) En développant et simplifiant l’équation, on obtient :

Donc l’équation admet deux solutions $x_1 = -\frac{1}{2}$ et .

e) En développant et simplifiant l’équation, on obtient :

Donc l’équation admet une solution unique $x = \frac{9}{4}$ .

EXERCICE 3 :

a) $x^2-12 = (x+ \sqrt{12})(x-\sqrt{ 12}) = (x+2 \sqrt{3})(x-2 \sqrt{3})$

EXERCICE 4 :

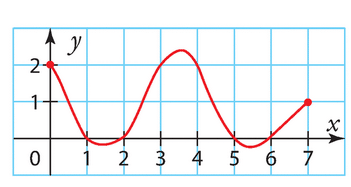
a) En suivant la courbe, on peut estimer que la solution de l’équation f(x)=2 est environ x=4.

b) On peut voir que la courbe coupe l’axe des x à deux endroits, environ aux points x=1 et x=6. Donc les solutions de l’équation f(x)=0 sont x = 1 et x = 6.

c) La courbe ne coupe pas l’axe des y à la valeur . Il n’y a donc pas de solution à cette équation.

d) On peut estimer que la solution de l’équation est environ .

EXERCICE 5 :

a) Le dénominateur ne peut pas être nul, donc 10-x≠0, c’est-à-dire x≠10. Par conséquent, l’ensemble de définition est : ℝ\{10} (l’ensemble des réels excepté 10).

b) L’expression sous la racine doit être positive ou nulle, donc x≥0. L’ensemble de définition est donc : [0,+∞[ (l’intervalle semi-ouvert à droite de 0, incluant 0).

c) Il n’y a pas de restriction sur x. L’ensemble de définition est donc : ℝ (l’ensemble des réels).

d) Le dénominateur ne peut pas être nul, donc x≠0. Par conséquent, l’ensemble de définition est : ℝ\{0} (l’ensemble des réels excepté 0).

EXERCICE 6 :

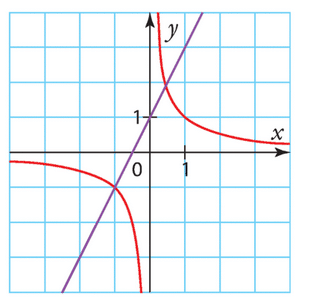
1. La courbe associée à la fonction inverse f est la courbe en bleu, et la courbe associée à la fonction affine g est la droite en rouge.

2. Pour résoudre graphiquement l’équation $\frac{1}{x}= 2x +1$ , il faut trouver l’intersection entre la courbe de f et la droite de g.

Visuellement, on voit qu’il y a une intersection entre ces deux courbes approximativement au point de coordonnées .

On peut alors confirmer cette solution en vérifiant que $\frac{1}{-0.6}= 2(-0.6) +1$ , ce qui est bien vérifié.

3.
a) On développe l’expression :

b) On peut retrouver algébriquement le résultat obtenu à la question 2 en résolvant l’équation $\frac{1}{x}= 2x +1$ :

$\frac{1}{x}= 2x +1 \Leftrightarrow 1= 2x^2 +x$
$\Leftrightarrow 2x^2 +x - 1 = 0$

On retrouve bien l’expression précédemment obtenue en développant cette équation. Les solutions de cette équation sont :

$x_1 = \frac{-1 + \sqrt{9}}{4} = \frac{1}{2}$
$x_2 = \frac{-1 - \sqrt{9}}{4} = -1$

Ces solutions sont également visibles graphiquement en regardant l’intersection entre la courbe f et l’axe horizontal (correspondant à y=0).

EXERCICE 7 :

On développe chaque membre de l’équation :

On peut résoudre cette équation pour trouver :

$x_1 = -\frac{7}{2}$

$x_2 = \frac{1}{2}$

Donc l’équivalence est fausse, car l’équation obtenue n’implique pas que .

Pour que l’équation de droite devienne équivalente à l’équation de gauche, on peut ajouter simplement l’équation $x+5 \neq -1$ , qui correspond à la restriction d’ensemble de définition de la fraction $\frac{3x - 2}{x + 1}$ . L’énoncé modifié serait donc :

$(x+5)(x+1) = (3x-2)(x+1) \Leftrightarrow (x+5 \neq -1) \land (x+5=3x-2)$

On développe chaque membre de l’équation :

$(x+3)(x^2+1) = (x^2+1)(4x-1)$

$x^3 + 3x^2 + x + 3 = 4x^3 – x^2 + 4x – 1$

$3x^3 – 4x^2 + x + 4 = 0$

On peut résoudre cette équation pour trouver :

$x \approx -1.0087$

$x \approx -0.2971 + 0.4259i$

$x \approx -0.2971 – 0.4259i$

Donc l’équivalence est fausse, car l’équation obtenue n’implique pas que $x+3=4x-1$.

Il n’y a pas de modification à apporter à l’équation de droite pour obtenir une équivalence avec l’équation de gauche, car l’équation de gauche ne peut pas être simplifiée de façon similaire à l’équation de droite.

On développe chaque membre de l’équation :

$(2x-3)^2 = (3x-1)^2$

$4x^2 – 12x + 9 = 9x^2 – 6x + 1$

On peut résoudre cette équation pour trouver :

$x_1 = \frac{3}{5}$

$x_2 = -\frac{8}{5}$

Donc l’équivalence est fausse, car l’équation obtenue n’implique pas que .

Pour que l’équation de droite devienne équivalente à l’équation de gauche, on peut ajouter simplement l’équation $2x-3\geq\, 0$, qui correspond à la restriction d’ensemble de définition de la racine carrée $(2x-3)^2$. L’énoncé modifié serait donc :

$(2x-3)^2 = (3x-1)^2 \Leftrightarrow (2x-3 \geq\, 0) \land (2x-3 = 3x-1)$

EXERCICE 8 :

a) L’équation $(x+4)(x-7)=0$ est vérifiée si et seulement si l’un des facteurs est nul. Donc on doit résoudre les deux équations :

$x+4 = 0$ ce qui donne $x=-4$

$x-7 = 0$ ce qui donne $x=7$

Les solutions de l’équation initiale sont donc $x=-4$ et $x=7$.

b) L’équation est vérifiée si et seulement si l’un des facteurs est nul. Donc on doit résoudre les deux équations :

$2x+3 = 0$ ce qui donne $x=-\frac{3}{2}$

$4x-5 = 0$ ce qui donne $x=\frac{5}{4}$

Les solutions de l’équation initiale sont donc $x=-\frac{3}{2}$ et $x=\frac{5}{4}$ .

c) L’équation $-x(5-4x)=0$ est vérifiée si et seulement si l’un des facteurs est nul. Donc on doit résoudre les deux équations :

$x = 0$

ce qui donne $x=\frac{5}{4}$

La solution de l’équation initiale est donc ou $x=\frac{5}{4}$ .

d) L’équation est vérifiée si et seulement si l’un des facteurs est nul. Donc on doit résoudre les deux équations :

$-15x+3 = 0$ ce qui donne $x=\frac{1}{5}$

$3x+9 = 0$ ce qui donne $x=-3$

Les solutions de l’équation initiale sont donc $x=\frac{1}{5}$ et $x=-3$.

e) L’équation $(2x-4)^2=0$ est vérifiée si et seulement si le carré du facteur est nul, c’est-à-dire si le facteur est zéro. Donc on doit résoudre l’équation :

$2x-4 = 0$ ce qui donne $x=2$

La solution de l’équation initiale est donc $x=2$.

f) L’équation est vérifiée si et seulement si l’un des facteurs est nul. Donc on doit résoudre les deux équations :

$3x = 0$ ce qui donne

$x-5 = 0$ ce qui donne $x=5$

Les solutions de l’équation initiale sont donc $x=0$ et $x=5$.

EXERCICE 9 :

a) On factorise : 5x(x-6/5)=0.

Donc soit x=0 soit x=6/5.

b) On factorise par (x+4) :

Donc , soit .

Donc soit x=-4 soit x=4/3.

c) On développe les produits et on simplifie : .

Cette équation n’a pas de solutions réelles car son discriminant $\Delta=(-35)^2-4(3)(35)=-455$ est négatif.

d) On factorise : . Donc soit x=-1.

EXERCICE 10 :

a) On a si et seulement si x=±9.

b) L’équation n’a pas de solutions réelles car son discriminant Δ=4(7) est positif.

c) L’équation a pour solutions x=±√15.

d) On divise les deux membres de l’équation 3x^2=48 par 3 pour obtenir x^2=16, qui a pour solutions x=±4.

e) On soustrait 20 des deux côtés de l’équation pour obtenir 2x^2=-20, puis on divise les deux côtés par 2 pour obtenir x^2=-10. Cette équation n’a pas de solutions réelles car son discriminant Δ=4(10) est positif.

f) On ajoute 2 des deux côtés de l’équation 4x^2-2=1 pour obtenir 4x^2=3, puis on divise les deux côtés par 4 pour obtenir x^2=3/4. Cette équation a pour solutions x=±√3/2.

EXERCICE 11 :

a) On reconnaît l’identité remarquable , donc l’équation est équivalente à (x+3)^2=0, qui a pour solution x=-3.

b) On utilise la formule de la racine carrée : $x=\frac{1}{72}(12\pm\sqrt{12})$ . Cependant, comme le discriminant de l’équation est positif, on ne peut pas simplifier davantage en nombre rationnel.

c) On factorise l’équation pour obtenir x(x-8)=0, donc les solutions sont x=0 et x=8.

d) On divise les deux côtés de l’équation 5(2x+1)^2=20 par 5 pour obtenir (2x+1)^2=4, donc les solutions sont x=-3/2 et x=1/2.

e) On développe les carrés pour obtenir , ce qui équivaut à 9x^2-102x+20=0. On utilise la formule de la racine carrée pour trouver les solutions : $x=\frac{51\pm\sqrt{1981}}{9}$ .

f) On ajoute 100 des deux côtés de l’équation (x-2)^2-100=0 pour obtenir (x-2)^2=100, puis on utilise la formule de la racine carrée pour obtenir x=2±10. Les solutions sont donc x=-8 et x=12.

EXERCICE 12 :

a) On élève les deux côtés de l’équation à la puissance 2 pour obtenir x=144.

b) L’équation $\sqrt{x}=-2$ n’a pas de solutions réelles car le carré d’un nombre réel est toujours positif.

c) On élève les deux côtés de l’équation à la puissance 2 pour obtenir .

d) On divise les deux côtés de l’équation $3\sqrt{x}=21$ par 3 pour obtenir $\sqrt{x}=7$ , puis on élève les deux côtés à la puissance 2 pour obtenir x=49.

EXERCICE 13 :

a) On résout l’équation en soustrayant x et en ajoutant 1 des deux côtés pour obtenir x=7.

b) On résout l’équation en divisant les deux côtés par 9 et en soustrayant 6 pour obtenir $x=-\frac{5}{3}$ .

c) On résout l’équation en développant le produit et en isolant les termes en x d’un côté de l’équation pour obtenir 5x=12 , donc $x=\frac{12}{5}$ .

d) On multiplie les deux côtés de l’équation $\frac{x+1}{x-1}=\frac{1}{2}$ par (x-1) pour obtenir x+1=\frac{x-1}{2}, ce qui équivaut à 3x=3, donc x=1. Cependant, il faut vérifier que x=1 n’est pas une solution exclue de l’équation initiale. En effet, on peut remplacer x par 1 dans \frac{x+1}{x-1} et on trouve \frac{2}{0}, qui n’est pas défini. Donc, l’équation n’a pas de solution.

EXERCICE 14 :

1. Pour estimer le nombre de bactéries au bout d’un jour, il suffit de remplacer t par 1 dans la fonction N(t) :
$N(1) = (0,5 \times 1 + 1)^2 = 2,25$ milliers de bactéries.
Donc on estime qu’il y a environ 2 250 bactéries au bout d’un jour.

2. Pour trouver le temps auquel le nombre de bactéries atteint 16 000, on doit résoudre l’équation N(t) = 16 :
(0,5t + 1)² = 16
0,5t + 1 = √16
0,5t + 1 = 4 ou 0,5t + 1 = -4 (mais cette dernière solution est impossible)
0,5t = 3
t = 6
Donc le nombre de bactéries atteint 16 000 au bout de 6 jours.

EXERCICE 15 :

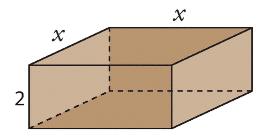
1. La boîte en question a une surface extérieure constituée de 5 faces : la base carrée, deux faces carrées latérales et deux faces rectangulaires représentant le couvercle et sa base.

La surface de la base carrée est x², la surface des deux faces carrées latérales est $2x \times 2$ , et la surface des deux faces rectangulaires est $2x \times 2$ .

Donc la surface extérieure totale est :

Mais la hauteur de la boîte est égale à 2, donc les dimensions des deux faces rectangulaires sont (x+4) et 2, et non pas 2x et 2. Donc la formule correcte est :
$S(x) = x^2 + 4x + 2(x+4) \times 2$

Donc la surface extérieure de la boîte est donnée en fonction de x par la formule .

2. Pour trouver quelle(s) valeur(s) de x donnent une surface extérieure de 72, il suffit de résoudre l’équation :
x² + 12x + 16 = 72
x² + 12x – 56 = 0
On peut résoudre cette équation en utilisant la formule quadratique, mais elle admet des solutions entières :
x = 4 ou x = -14
Comme x représente une longueur positive, la seule solution acceptable est x = 4. Donc la boîte en question a une base carrée de côté 4 pour avoir une surface extérieure de 72.

EXERCICE 16 :

Les droites (AB) et (CD) sont parallèles si et seulement si leurs coefficients directeurs sont égaux. Les coefficients directeurs des droites passant par deux points et sont donnés par la formule :
$a = \frac{y_2 - y_1}{x_2 - x_1}$
Donc pour que les droites (AB) et (CD) soient parallèles, il faut que :

où sont les coefficients directeurs des droites (AB), (AC), (CD) et (BC), respectivement.

On peut appliquer cette formule pour trouver la condition à vérifier en fonction de x pour que les droites (AB) et (CD) soient parallèles.

Mais sans plus d’informations sur les points A, B, C et D, on ne peut pas répondre à cette question de manière précise.

EXERCICE 17 :

1) Pour x = 0, on a y = 1 et donc :
$A = 3(0^2+1^2) - 4(0+1) + 6 \times 0\times 1 = -1$
Pour x = -2, on a y = 3 et donc :
$A = 3((-2)^2+3^2) - 4((-2)+3) + 6 \times (-2) \times 3 = -37$

2) On développe :

Donc

Mais on sait que x+y = 1 , donc

Si x+y = 1, alors et donc . On a également x+y = 1, donc xy ≤ 1/4 par inégalité arithmético-géométrique. Donc 10xy ≤ 5 et donc 3 – 10xy ≥ -2. Donc si x+y = 1, on a -2 ≤ A ≤ 3.

Mais on sait également que A = (3 – 10xy)(1-x-y), donc si x+y = 1, alors 3 – 10xy = 1-x-y et donc A = -1. Ainsi, si x+y = 1, alors A est toujours égal à -1.

Voir Corrigés 11 à 17...

Télécharger puis imprimer cette fiche en PDF.

Télécharger ou imprimer cette fiche «corrigé des exercices sur les équations en 2de.» au format PDF afin de pouvoir travailler en totale autonomie.