Corrigé sur des exercices sur les fonctions en 2de.

EXERCICE 1 :

1)a) On calcule $f(1+5\sqrt{2})$ :
$f(1+5\sqrt{2}) = -\frac{4}{5}(1+5\sqrt{2})^2 + 3(1+5\sqrt{2}) + 5 \\\\= -\frac{4}{5}(1+2\cdot5\sqrt{2}+50)+3+15\sqrt{2}+5 \\\\= -\frac{4}{5}\cdot51-4\cdot5\sqrt{2}+18\sqrt{2}+8 \\\\= -\frac{204}{5}+14\sqrt{2}$

On peut donc écrire : $f(1+5\sqrt{2}) = -\frac{204}{5} + 14\sqrt{2}$

b) On calcule $f(5-\sqrt{3})$ :
$f(5-\sqrt{3}) = -\frac{4}{5}(5-\sqrt{3})^2 + 3(5-\sqrt{3}) + 5 \\\\= -\frac{4}{5}(28-10\sqrt{3}) + 15 - 3\sqrt{3} + 5 \\\\= -\frac{112}{5} + \frac{40}{5}\sqrt{3} + 17 - 3\sqrt{3} \\\\= -\frac{145}{5} - \sqrt{3}$

On peut donc écrire : $f(5-\sqrt{3}) = -\frac{145}{5} - \sqrt{3}$

2) Pour f(x) = 1, on a :
$-\frac{4}{5}x^2 + 3x + 5 = 1 \\-\frac{4}{5}x^2 + 3x + 4 = 0$
On peut résoudre cette équation en utilisant la formule de la discriminante :
$\Delta = 3^2 - 4 \times (-\frac{4}{5}) \times 4 = \frac{121}{5} > 0$
Les racines de l’équation sont alors :
$x_1 = \frac{-3+\sqrt{\frac{121}{5}}}{-\frac{8}{5}} \approx -0,157$
$x_2 = \frac{-3-\sqrt{\frac{121}{5}}}{-\frac{8}{5}} \approx 5,013$
Donc il n’y a pas de réel x tel que f(x) = 1.

Pour f(2) et f(0), on calcule :
$f(2) = \frac{4 \times 2+2}{1+2^2} = \frac{10}{5} = 2$
$f(0) = \frac{4 \times 0+2}{1+0^2} = 2$
Donc les images de 2 et de 0 par f sont égales.

3) On calcule $f(\frac{1}{2})$ :
$f(\frac{1}{2}) = \frac{4\cdot\frac{1}{2}+2}{1+\frac{1}{4}} = \frac{4+2}{\frac{5}{4}} = \frac{24}{5}$

4) On résout l’équation f(x) = 0 :
$-\frac{4}{5}x^2 + 3x + 5 = 0$
On utilise la formule de la discriminante :
$\Delta = 3^2 - 4 \times (-\frac{4}{5}) \times 5 = \frac{89}{5} > 0$
Les racines de l’équation sont alors :
$x_1 = \frac{-3+\sqrt{\frac{89}{5}}}{-\frac{8}{5}}$
$x_2 = \frac{-3-\sqrt{\frac{89}{5}}}{-\frac{8}{5}}$
Donc les antécédents de 0 sont et .

EXERCICE 2 :

1. On calcule f(3) :
$f(3)=\frac{4 \times 3 + 2}{1+3^2} = \frac{14}{10} = \frac{7}{5}.$
Donc f(3) n’est pas égal à 1.

2. On calcule f(2) et f(0) :
$f(2)=\frac{4\times 2+2}{1+2^2} = \frac{10}{5} = 2$
$f(0)=\frac{4\times 0+2}{1+0^2} = 2$
On a donc f(2) = f(0) = 2.

3. On calcule $f(\frac{1}{2})$ :
$f(\frac{1}{2})=\frac{4\times \frac{1}{2} + 2}{1+(\frac{1}{2})^2} = \frac{5}{2}$ .
L’image de $\frac{1}{2}$ par f est donc égale à $\frac{5}{2}$ .

4. On cherche les antécédents de 0 par f, c’est-à-dire les valeurs de x telles que .
On résout l’équation $\frac{4x+2}{1+x^2}=0$ :
$4x+2=0 \Leftrightarrow x=-\frac{1}{2}$ .
La seule solution est donc $x=-\frac{1}{2}$ .
L’antécédent de 0 par f est donc $-\frac{1}{2}$ .

EXERCICE 3 :

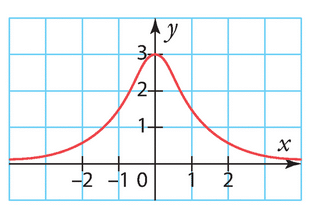
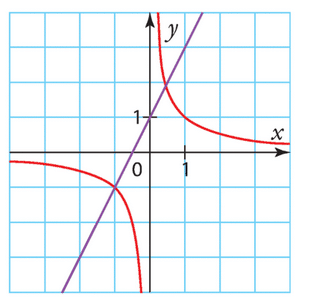
a) En lisant graphiquement, on trace une droite verticale passant par x=-1 et on cherche l’intersection avec la courbe. Cette intersection se situe à environ y=1.3. Donc l’image de -1 par f est environ 1.3.

b) En lisant graphiquement, on cherche la valeur de f(0) en lisant l’ordonnée en x=0 sur la courbe, qui est environ y=2. Donc l’image de 0 par f est environ 2.

c) En lisant graphiquement, on trace une droite horizontale passant par y=1 et on cherche les intersections avec la courbe. Il y en a deux, environ en $x=-\frac{3}{2}$ et x=2. Donc les antécédents de 1 par f sont environ $x=-\frac{3}{2}$ et x=2.

d) En lisant graphiquement, on trace une droite horizontale passant par y=3 et on cherche les intersections avec la courbe. Il y a une seule intersection, environ en x=3. Donc l’antécédent de 3 par f est environ x=3.

EXERCICE 4 :

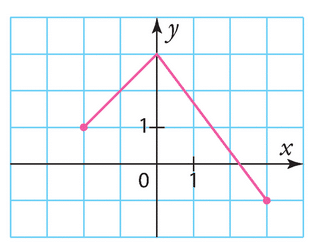
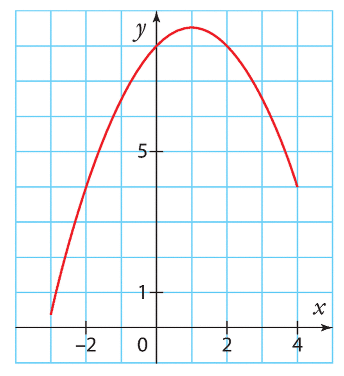
a) En lisant graphiquement, on trouve que g(0) est environ 0.5.

b) En lisant graphiquement, on cherche les valeurs de g(1) et g(-2) en lisant les ordonnées en x=1 et x=-2 sur la courbe. On trouve que g(1) est environ -1 et que g(-2) est environ -1.5.

c) En lisant graphiquement, pour trouver les antécédents éventuels de -1, on trace une droite horizontale passant par y=-1 et on cherche les intersections avec la courbe. Il y a deux intersections, environ en x=-1.5 et x=2. Donc les antécédents éventuels de -1 sont environ -1.5 et 2.

Pour trouver les antécédents éventuels de 1, on trace une droite horizontale passant par y=1 et on cherche les intersections avec la courbe. Il n’y a pas d’intersection.

Pour trouver les antécédents éventuels de 5, on trace une droite horizontale passant par y=5 et on cherche les intersections avec la courbe. Il n’y a pas d’intersection.

EXERCICE 5 :

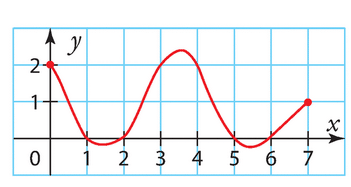
a) En estimant sur la courbe, on peut voir que f(x)=2 a deux solutions approximativement égales à 2,5 et 6,5.

b) f(x)=0 a trois solutions approximativement égales à 1,5, 3,5 et 6.

c) f(x)=-1 a une solution approximativement égale à 5,5.

d) f(x)=1 a deux solutions approximativement égales à 1 et 5.

EXERCICE 10 :

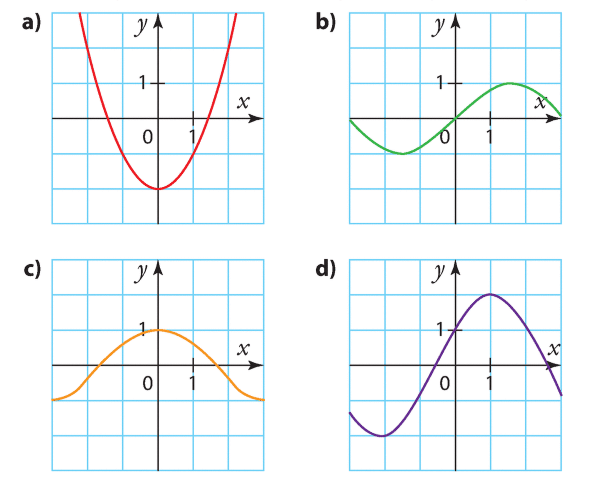
La première courbe est une fonction paire.
La deuxième courbe n’est ni paire, ni impaire.
La troisième courbe est une fonction impaire.

EXERCICE 11 :

a) La fonction est définie pour tout x sauf pour x = 10 car le dénominateur est nul.
b) g(x) >= 0 pour tout x et le domaine de définition de g est $[0;+\infty[$ .
c) h(x) est définie pour tout x et son domaine de définition est $[-3;+\infty[$ .
d) i(x) est définie pour tout x différent de 0 et son domaine de définition est $\mathbb{R}^{*}$ .

EXERCICE 12 :

1. Les courbes associées aux fonctions sont la droite y = x/2 et la droite y=2x+1.
2. L’équation $\frac{1}{x} = 2x+1$ peut être réécrite sous forme . En résolvant cette équation, on obtient les solutions $x = -1+\sqrt{2}$ et $x = -1-\sqrt{2}$ .
3. a) .
b) $(2x-1)(x+1) = (x-\frac{1}{2})^2+\frac{5}{4}$ .
c) La parabole admet un sommet en $(-\frac{1}{2},\frac{5}{4})$ , donc la hauteur maximale atteinte par la balle est $\frac{5}{4}$ mètres.

EXERCICE 13 :

1. La fonction n’est pas définie en 2 donc l’image de 2 ne peut pas être déterminée.
2. La fonction n’est pas définie en -2 donc la valeur de f(-2) ne peut pas être déterminée.
3. Une valeur approchée des antécédents de 5 est 0,78 et 3,22.
4. f(x) = 4 est équivalent à . En résolvant cette équation, on obtient les solutions $x = 1-\sqrt{\frac{2}{3}}$ et $x = 1+\sqrt{\frac{2}{3}}$ .
5. f(x) < 6 est équivalent à .

En résolvant cette inéquation, on obtient $1-\sqrt{\frac{10}{3}} < x < 1+\sqrt{\frac{10}{3}}$ .
6. $f(x) \geq\,\, 8$ est équivalent à $-3x^2+6x-12 \geq\,\, 0$ .

Cette inéquation est équivalente à $x \leq\,\, 1-\sqrt{\frac{2}{3}}$ ou $x \geq\,\, 1+\sqrt{\frac{2}{3}}$ .

On peut aussi dire que le complémentaire de l’ensemble des antécédents de 8 est l’intervalle $[1-\sqrt{\frac{2}{3}};1+\sqrt{\frac{2}{3}}]$ .

EXERCICE 14 :

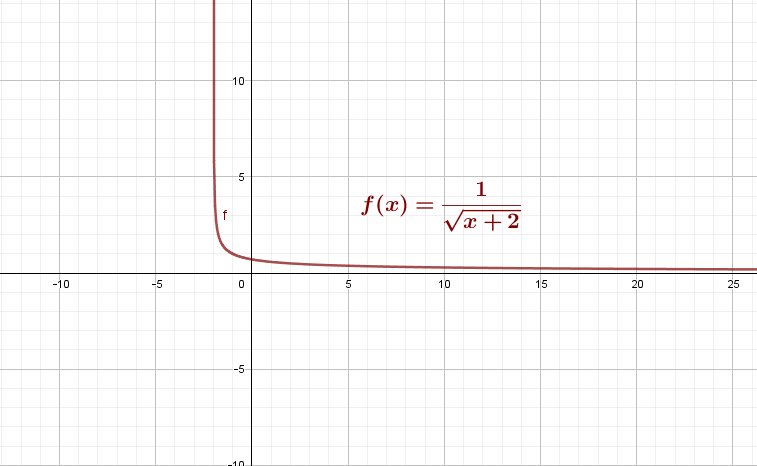
1) Df est l’ensemble des réels tels que x+2>0, soit $D_f = ]-2, +\infty[$ .

2) On calcule :

– $f(-1) = \frac{1}{\sqrt{1}} = 1$ ;
– $f(7) = \frac{1}{\sqrt{9}} = \frac{1}{3}$ ;
– n’est pas défini car n’appartient pas à .

Donc, $f(-1) = 1, f(7) =\frac{ 1}{3}$ et f(-4) n’est pas défini.

3) Le ou les antécédents de 2 sont les solutions de l’équation , c’est-à-dire :

$2 = \frac{1}{\sqrt{x+2}}$ ⇔ $x+2 = \frac{1}{4}$ ⇔ $x = -\frac{15}{4}$ .

Donc, le seul antécédent de 2 est $-\frac{15}{4}$ .

4) Le ou les antécédents de -1 sont les solutions de l’équation f(x) = -1, c’est-à-dire :

$-1 = \frac{1}{\sqrt{x+2}}$ ⇔ ⇔ .

Donc, le seul antécédent de -1 est -1.

5) Voici le graphique de f :

EXERCICE 15 :

a) f(x) est définie si et seulement si .

Factorisons le polynôme : .

Le polynôme est négatif entre les racines, soit sur l’intervalle ]-1 ; 3[. Donc l’ensemble de définition de f est Df = ]-∞, -1[ U ]3, +∞[.

b) Pour déterminer l’image de 0, on calcule $f(0) = \frac{1}{-4} = -\frac{1}{4}$ .

Pour déterminer l’image de 2π, on calcule $f(2\pi) = \frac{1}{2\pi-\pi} = \frac{1}{\pi}$ .

c) Pour déterminer le ou les antécédents de 2, on résout l’équation $f(x) = \frac{2 }{2} = \frac{1}{x-\pi}$ ,

soit $x-\pi = \frac{1}{2}$ , donc $x = \frac{3}{2} +\pi$ . Le seul antécédent de 2 est donc $x = \frac{3}2{ + \pi$ .

Pour déterminer le ou les antécédents de 0, on résout l’équation f(x) = 0 : $0 = \frac{1}{x-\pi}$ ,

soit x-π = ∞, donc x = ∞ + π ou x = -∞ + π.

Il n’y a pas d’antécédent de 0.

d) Pour déterminer le signe de f, on étudie le signe de l’expression x-π. Si x-π > 0, alors f(x) est négatif, si x-π < 0, alors f(x) est positif. On peut résumer cela par :

– f(x) < 0 si x > π ;
– f(x) > 0 si x < π.

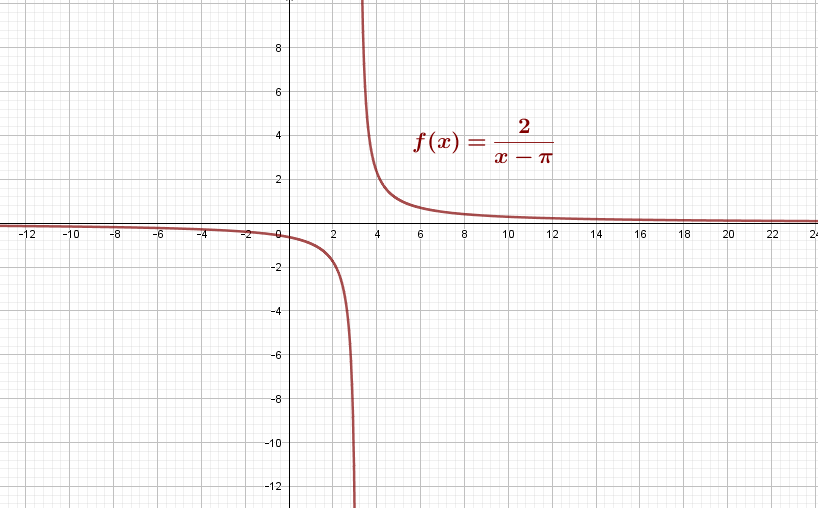
e) Le graphique de f est le suivant :

La courbe est une hyperbole d’asymptotes verticales x = π et x = -1, passant par le point (0,-1/4).

EXERCICE 16 :

On définit la fonction f sur ℝ par $x\,\mapsto \,\sqrt{2}x-\sqrt{3}$

1) L’image de $- \sqrt{2}$ par f est $f(- \sqrt{2}) = - \sqrt{6} - \sqrt{3}$ .

2) Pour déterminer les antécédents de 0 et $\sqrt{2}$ , on résout respectivement les équations et $f(x) = \sqrt{2}$ :

– f(x) = 0 ⇔ $x = \frac{\sqrt{3}}{\sqrt{2}}$ .
– $f(x) = \sqrt{2}$ ⇔ $\sqrt{2}x - \sqrt{3} = \sqrt{2}$ ⇔ $x = \frac{\sqrt{2} + \sqrt{3}}{2}$ ou $x = \frac{-\sqrt{2} + \sqrt{3}}{2}$ .

Donc, l’antécédent de 0 est √3/√2, et les antécédents de √2 sont $x = \frac{\sqrt{2} + \sqrt{3}}{2}$ et $x = \frac{-\sqrt{2} + \sqrt{3}}{2}$ .

3) Pour tout réel x, on a $f(x) = \sqrt{2}x - \sqrt{3}$ .

Le coefficient √2 étant positif, le signe de f(x) est le même que celui de $x - \frac{\sqrt{3}}{\sqrt{2}}$ .

En utilisant la valeur de l’antécédent de 0, on peut en déduire que f(x) est négatif si et seulement si $x < \frac{\sqrt{3}}{\sqrt{2}}$ , et positif si et seulement si $x > \frac{\sqrt{3}}{\sqrt{2}}$ .

Donc, f est positive sur l’intervalle $]\frac{\sqrt{3}}{\sqrt{2}};+\infty[$ et négative sur l’intervalle $]-\infty;\frac{\sqrt{3}}{\sqrt{2}}[$ .

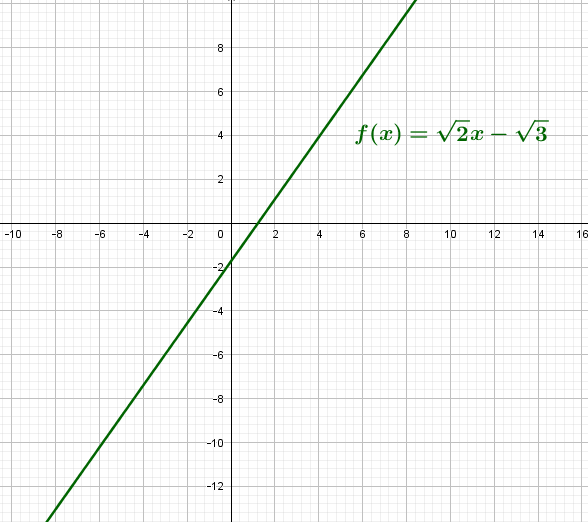
4) Voici le graphique de f :

Voter pour post

Télécharger puis imprimer cette fiche en PDF.

Télécharger ou imprimer cette fiche «corrigé des exercices sur les fonctions en 2de.» au format PDF afin de pouvoir travailler en totale autonomie.

D'autres cours et exercices à consulter

Mathématiques Web c'est 2 268 522 fiches de cours et d'exercices téléchargées.