Logarithme népérien : cours de maths en terminale en PDF.

Le logarithme népérien avec un cours de maths en terminale. De plus, le logarithme népérien d’un nombre x peut aussi être défini comme la puissance à laquelle il faut élever e pour qu’on puisse obtenir x. En outre, la fonction logarithme népérien est ainsi la bijection réciproque de la fonction exponentielle.

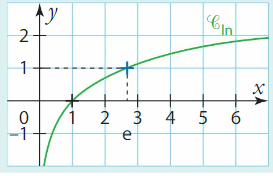
I. Fonction logarithme népérien, fonction réciproque de la fonction exponentielle.

Propriétés : la fonction exponentielle.

La fonction exponentielle est continue et strictement croissante sur $\mathbb{R}$ .
Nous avons $\lim_{x\to\,-\infty\,}e^x=0$ et $\lim_{x\to\,+\infty\,}e^x=+\infty$ .

L’équation e^x=k , avec $k\in\,\mathbb{R}^{+*}$ , admet alors une unique solution dans $\mathbb{R}$ , d’après le théorème des valeurs intermédiaires.

Définition : fonction logarithme népérien.

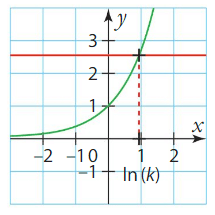
On appelle fonction logarithme népérien, notée , la fonction définie sur $]0;+\infty[$ qui à tout nombre réel strictement positif x associe l’unique solution de l’équation e^y=x d’inconnue .

On définit ainsi $y\,=\,ln\,(x)$ .

Exemple :

A l’aide de la touche de la calculatrice, on peut vérifier que $ln\,(2)\,\simeq\,0,693$ .

Remarque :

Quand il n’y a pas d’ambiguïté, on peut noter au lieu de .

Propriétés : fonction logarithme népérien.

Pour tout réel $x>0,e^{lnx}=x$
Pour tout réel
$ln(\frac{1}{e})=-lne=-1$

Exemple :

et $e^{ln3}=3$ .

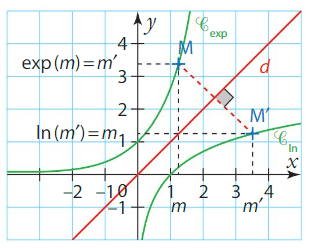
II. Courbes des fonctions logarithme népérien et exponentielle

Propriété :

Dans un repère orthonormé, les courbes représentatives des fonctions et exp sont symétriques par rapport à la droite d’équation y= x.

III. Sens de variation de la fonction logarithme népérien

Propriété :

La fonction est strictement croissante sur $]0;+\infty[$ .

Démonstration :

Soient a et b deux nombres réels strictement positifs.
$0<a<b\Leftrightarrow\,0<e^{ln(a)}<e^{ln(b)}$ .

On en déduit $ln\,(a)\,<\,ln\,(b)$ car la fonction $x\,\mapsto \,e^x$ est strictement croissante sur $\mathbb{R}$ .

Propriétés :

Pour tous réels a > O et b > O : $ln(a)=\,ln(b)\,\Leftrightarrow\,a=b\,\,et\,ln\,(a)\,<\,ln\,(b)\,\Leftrightarrow\,a\,<\,b$ .

Preuve :

• $ln(a)=ln(b)\Leftrightarrow\,e^{ln(a)}=e^{ln(b)}\Leftrightarrow\,a=b$ car la fonction $x\,\mapsto \,e^x$ est strictement croissante sur $\mathbb{R}$ .
• $ln(a)<ln(b)\Leftrightarrow\,e^{ln(a)}<e^{ln(b)}\Leftrightarrow\,a<b$ car la fonction $x\,\mapsto \,e^x$ est strictement croissante sur $\mathbb{R}$ .

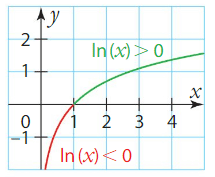
Remarque :

$ln(x)>0\Leftrightarrow\,x>1$ et $ln(x)<0\Leftrightarrow\,0<x<1$ .

IV. Propriétés algébriques de la fonction logarithme népérien

1.Relation fonctionnelle.

Propriété :

Pour tous réels a et b strictement positifs :
$ln(ab)\,=\,ln(a)\,+\,ln(b)$ .

Preuve :

Pour tous réels a et b strictement positifs, $e^{ln(ab)}=ab=e^{ln(a)}\times \,e^{ln(b)}=e^{ln(a)+ln(b)}$
soit $e^{ln(ab)}=e^{ln(a)+ln(b)}$ .
On a donc $ln(ab)\,=\,ln(a)\,+\,ln(b)$ .

Remarques :

On retrouve la particularité que cette fonction transforme les produits en sommes.
Cette formule se généralise à un produit de plusieurs facteurs.

Exemples :

$ln\,(10)\,=\,ln\,(5\,\times \,2)\,=\,ln\,(5)\,+\,ln(2)$
$ln\,(30)\,=\,ln\,(2\times \,3\,\times \,5)\,=ln\,(2)\,+\,ln\,(3)\,+\,ln\,(5)$

2. Logarithme d’un inverse et d’un quotient.

Propriété :

Pour tous réels a et b strictement positifs :

$ln(\frac{a}{b})=ln(a)-ln(b)$ et $ln(\frac{1}{a})=-ln(a)$ .

Preuve :

Pour tout nombre réel a strictement positif :

$ln(1)=ln(\frac{a}{a})=ln(a\times \,\frac{1}{a})=lna+ln(\frac{1}{a})$ d’où $ln(a)+ln(\frac{1}{a})=0$

ainsi, nous avons $ln(\frac{1}{a})=-ln(a)$ .

Pour tous nombres réels a et b strictement positifs:

$ln(\frac{a}{b})=ln(a\times \,\frac{1}{b})=ln(a)+ln(\frac{1}{b})=ln(a)-ln(b)$ .

3. Logarithme d’une puissance, d’une racine carrée.

Propriété :

Pour tout réel a strictement positif, et pour tout entier relatif n :

$ln(a^n)\,=\,nln(a)$ et $ln(\sqrt{a})=\frac{1}{2}ln(a)$ .

Exemples :

$ln(\sqrt{6})=ln(6^{\frac{1}{2}})=\frac{1}{2}ln(6)$ .

V. Étude de la fonction logarithme népérien

1.Dérivée de la fonction logarithme népérien.

Propriété :

La fonction est dérivable sur $]0;+\infty[$ et, pour tout réel x>0 , $ln'(x)=\frac{1}{x}$ .

Preuve :
On admet que la fonction est dérivable sur $]0;+\infty[$ .

Pour tout réel , on pose $f(x)=e^{ln(x)}$ .
La fonction étant dérivable sur $]0;+\infty[$ et la fonction exponentielle étant dérivable sur $\mathbb{R}$ ,

f est aussi dérivable sur $]0;+\infty[$ comme composée de fonctions dérivables.
Sachant que $(vou)'=(v'ou)\times \,u'$ , en posant et $u(x)\,=\,ln(x)$ , on a alors :
$f'(x)=e^{ln(x)}\times \,ln'(x)=x\times \,ln'(x)$ .
On a également donc .
Par conséquent, on a $x\times \,ln'(x)=1\Leftrightarrow\,ln'(x)=\frac{1}{x}$ .

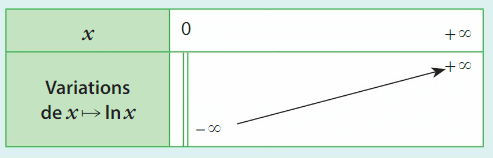
2.Limites aux bornes de l’ensemble de définition.

Propriétés :

$\lim_{x\to\,+\infty}ln(x)=+\infty$ et $\lim_{x\to\,0}ln(x)=-\infty$

3.Tableau de variations de et courbe représentative.

Propriété :

4.Croissance comparée.

Propriété :

$\lim_{x\to\,+\infty}\frac{lnx}{x}=0\,;\,\,\lim_{x\to\,0}xlnx=0;\lim_{x\to\,+\infty}\frac{lnx}{x^n}=0\,(n\in\mathbb{N}^*)\,;\,\,\lim_{x\to\,0}x^nlnx=0\,(n\in\mathbb{N}^*)$

5. Fonction composée ln (u).

Propriété : dérivée de ln u.

Soit u une fonction dérivable et strictement positive sur un intervalle l.
La fonction lnu est alors dérivable sur I et $(ln\,u)'\,=\frac{u'}{u}$

Propriété : sens de variation de ln(u).

Soit u une fonction dérivable et strictement positive sur un intervalle l.
Les fonctions u et lnu ont le même sens de variation sur l.

Preuve :

u étant strictement positive, le signe de $\frac{u'}{u}$ est le même que celui de .

Or $(ln\,u)'\,=\frac{u'}{u}$ , ce qui signifie que le signe de est le même que celui de ,

c’est-à-dire que u et ont même sens de variation.

Télécharger puis imprimer cette fiche en PDF.

Télécharger ou imprimer cette fiche «logarithme népérien : cours de maths en terminale en PDF.» au format PDF afin de pouvoir travailler en totale autonomie.

Vous devez vous inscrire ou vous connecter à votre compte afin de pouvoir télécharger ce document au format PDF.