Corrigé des exercices sur la trigonométrie en 1ère.

EXERCICE 1 :

1) On a :

Donc g est une fonction paire, ce qui signifie que son graphe est symétrique par rapport à l’axe des ordonnées.

2) On a :

$g(x+\frac{\pi}{2})=cos(4(x+\frac{\pi}{2}))sin^2(4(x+\frac{\pi}{2}))=cos(4x+2\pi)sin^2(4x+2\pi)=cos(4x)sin^2(4x)=g(x)$

Donc g est une fonction $\frac{\pi}{2}$ -périodique, c’est-à-dire que son graphe se répète tous les $\frac{\pi}{2}$ .

EXERCICE 2 :

1) On a :

$g(-x)=cos(-x)+sin(-x)=cos(x)-sin(x)\neq g(x)$
$g(x+\pi)=cos(x+\pi)+sin(x+\pi)=-cos(x)-sin(x)\neq g(x)$

Donc g n’est ni paire ni impaire.

2) On a :

$g(x+2\pi)=cos(x+2\pi)+sin(x+2\pi)=cos(x)+sin(x)=g(x)$

Donc g est une fonction $2\pi$ -périodique, c’est-à-dire que son graphe se répète tous les $2\pi$ .

3) On remarque que :

$-1\leq\, cos(x)\leq\, 1$
$-1\leq\, sin(x)\leq\, 1$

Donc en ajoutant les deux inégalités, on obtient :

$-2\leq\, cos(x)+sin(x)\leq\, 2$

Donc pour tout réel x, $-2\leq\, g(x)\leq\, 2$ .

EXERCICE 3 :

1) On a $cos(\frac{\pi}{3})=\frac{1}{2}$ , donc $cos(-\frac{\pi}{3})=cos(\pi-\frac{\pi}{3})=-cos(\frac{\pi}{3})=-\frac{1}{2}$ .

De plus, $cos(\frac{2\pi}{3})=cos(\pi+\frac{\pi}{3})=-cos(\frac{\pi}{3})=-\frac{1}{2}$ .

2) On a $sin(-\frac{\pi}{3})=-sin(\frac{\pi}{3})=-\frac{\sqrt{3}}{2}$ .

De plus, $sin(\frac{2\pi}{3})=sin(\pi+\frac{\pi}{3})=-sin(\frac{\pi}{3})=-\frac{\sqrt{3}}{2}$ .

EXERCICE 4 :

1) On a $cos(x)=\frac{\sqrt{3}}{2}$ lorsque $x=\frac{\pi}{6}$ ou $x=\frac{11\pi}{6}$ (car cos est positif sur $[0,\pi]$ et $\frac{\sqrt{3}}{2}$ est l’une des valeurs que peut prendre cos à ces deux angles).

2) On a $sin(x)=\frac{\sqrt{2}}{2}$ lorsque $x=\frac{\pi}{4}$ ou $x=\frac{3\pi}{4}$ (car sin est positif sur $[\frac{\pi}{2},\frac{3\pi}{2}]$ et $\frac{\sqrt{2}}{2}$ est l’une des valeurs que peut prendre sin à ces deux angles).

EXERCICE 5 :

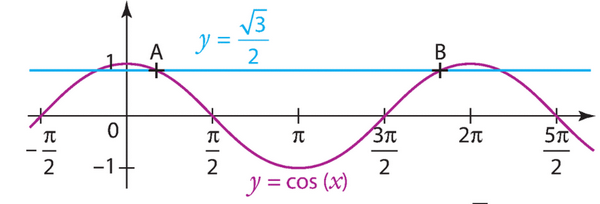
1. Les abscisses des points A et B sont respectivement $\frac{\pi}{3}$ et $\frac{2\pi}{3}$ .

2. Les solutions sur $[0;2\pi[$ de l’équation $cos(x)=\frac{\sqrt{3}}{2}$ sont $x=\frac{\pi}{6}$ et $x=\frac{11\pi}{6}$ .

3. Les solutions sur $[0;2\pi[$ de l’inéquation $cos(x) \leq\,\, \frac{\sqrt{3}}{2}$ sont $x\in[0,\frac{\pi}{6}]\cup[\frac{5\pi}{6},\pi]\cup[\frac{7\pi}{6},2\pi]$ .

EXERCICE 6 :

a) On a $f(x+1)=cos(2\pi(x+1))=cos(2\pi x+2\pi)=cos(2\pi x)=f(x)$ pour tout réel x, donc f est bien T-périodique avec T=1.

b) On a $f(x+\frac{2\pi}{3})=sin(3(x+\frac{2\pi}{3}))=sin(3x+2\pi)=sin(3x)=f(x)$ pour tout réel x, donc f est bien T-périodique avec $T=\frac{2\pi}{3}$ .

c) On a $f(x+\frac{2\pi}{7})=\frac{2}{3}cos(7(x+\frac{\pi}{4})+\frac{2\pi}{7})=\frac{2}{3}cos(7x+\frac{9\pi}{28})=\frac{2}{3}cos(7x+\frac{2\pi}{7})=f(x)$ pour tout réel x, donc f est bien T-périodique avec $T=\frac{2\pi}{7}$ .

d) On a $f(x+\frac{6\pi}{5})=\frac{10}{7}sin(\frac{5(x+\frac{6\pi}{5})-8}{3})=\frac{10}{7}sin(\frac{5x-2\pi}{3})=\frac{10}{7}sin(\frac{5x}{3})=f(x)$ pour tout réel x, donc f est bien T-périodique avec $T=\frac{6\pi}{5}$ .

EXERCICE 7 :

1.a) On a $\frac{91\pi}{4}=22\pi+\frac{\pi}{4}$ , donc x=-\frac{\pi}{4}.

b) $cos(\frac{91\pi}{4})=\cos(22\pi+\frac{\pi}{4})=\cos(\frac{\pi}{4})=\frac{\sqrt{2}}{2}$

et $sin(\frac{91\pi}{4})=\sin(22\pi+\frac{\pi}{4})=\sin(\frac{\pi}{4})=\frac{\sqrt{2}}{2}$ .

2.a) $cos(-\frac{13\pi}{6})=\cos(\frac{\pi}{6})=\frac{\sqrt{3}}{2}$ .

b) $sin(-\frac{81\pi}{2})=sin(40\pi-\frac{\pi}{2})=-sin(\frac{\pi}{2})=-1$ .

3.a) $cos(\frac{25\pi}{3})=\cos(8\pi+\frac{\pi}{3})=\cos(\frac{\pi}{3})=\frac{1}{2}$ , donc $sin(\frac{25\pi}{3})=\sin(\frac{\pi}{2}-\frac{\pi}{3})=\sin(\frac{\pi}{6})=\frac{1}{2}$ .

b) $sin(\frac{45\pi}{6})=\sin(\frac{15\pi}{2})=\sin(7\pi+\frac{\pi}{2})=\sin(\frac{\pi}{2})=1$ , donc $cos(\frac{45\pi}{6})=\cos(\frac{\pi}{2})=0$ .

EXERCICE 8 :

1.a) Comme f est définie sur $]-\pi ; \pi]$ , on a $-1 \leq\, X=cos(x) \leq\, 1$ .

b) En résolvant l’équation $4X^2\,+\,2(\sqrt{2}\,-\,l)X\,-\sqrt{2}=0$ , on trouve $X_1=\frac{-\sqrt{2}}{4\sqrt{2}-2}=-\frac{\sqrt{2}}{2}-\frac{1}{2}(\sqrt{2}-1)=\cos(\frac{3\pi}{4})$ et $X_2=\frac{\sqrt{2}}{2}-\frac{1}{2}(\sqrt{2}+1)=\cos(\frac{\pi}{4})$ .

c) Les solutions sur [-1,1] de l’équation $4X^2\,+\,2(\sqrt{2}\,-\,l)X\,-\sqrt{2}=0$ sont $X=\cos(\frac{\pi}{4})$ et $X=\cos(\frac{3\pi}{4})$ .

d) En utilisant le fait que cos(x)=X, on en déduit les solutions de l’équation f(x)=0 sur $]-\pi ; \pi]$ : $x=\frac{\pi}{4}+2k\pi$ et $x=\frac{3\pi}{4}+2k\pi$ pour $k\in\mathbb{Z}$ .

2. Les solutions sur [-1,1] de l’inéquation $4X^2\,+\,2(\sqrt{2}\,-\,l)X\,-\sqrt{2}>0$ sont

$X \in ]-\infty,\frac{-\sqrt{6}+\sqrt{2}}{4\sqrt{2}-2}[\cup]\frac{\sqrt{6}-\sqrt{2}}{4\sqrt{2}-2},\frac{-\sqrt{2}}{4}[\cup]\frac{\sqrt{2}}{4},\frac{\sqrt{6}+\sqrt{2}}{4\sqrt{2}-2}[\cup]\frac{-\sqrt{6}-\sqrt{2}}{4\sqrt{2}-2},+\infty[$ .

En utilisant le fait que , on en déduit les solutions de l’inéquation sur $]-\pi ; \pi]$ :

$x \in ]\arccos(\frac{-\sqrt{6}+\sqrt{2}}{4\sqrt{2}-2}),\arccos(\frac{\sqrt{6}-\sqrt{2}}{4\sqrt{2}-2})[\cup]\arccos(\frac{\sqrt{2}}{4}),\arccos(\frac{\sqrt{6}+\sqrt{2}}{4\sqrt{2}-2})[$ .

EXERCICE 9 :

1. Le disque tourne 33 tours et $\frac{1}{3}$ de tour par minute, donc il tourne pendant $60 \times 33\times \frac{1}{3}=\frac{2000}{3} min$ .

Chaque chanson a donc une durée de $\frac{\frac{2000}{3}}{6}= \frac{100}{3}$ min.

Le saphir se trouvera donc sur le demi-axe négatif à la fin de chaque chanson, c’est-à-dire après une durée de $\frac{100}{3}$ min.

2. Le disque tourne 16 tours et $\frac{2}{3}$ de tour par minute, donc il tourne pendant $16 \times 60+\frac{2}{3}= 962\times \frac{2}{3} s$ .

Chaque chanson a donc une durée de $5 \times 60=300 s$ .

a) Après 3 min=180 s, le saphir aura parcouru un angle de $\frac{180}{300} \times 2\pi=\frac{6}{5}\pi$ .

Il se trouvera donc sur le demi-axe positif.

b) Après 4 min=240 s, le saphir aura parcouru un angle de $\frac{240}{300} \times 2\pi=\frac{8}{5}\pi$ .

Il se trouvera donc sur le demi-axe négatif.

c) A la fin de la première chanson, le saphir aura parcouru un angle de $\frac{300}{300} \times 2\pi=2\pi$ .

Il reviendra donc à la position de départ sur le demi-axe positif.

d) A la fin de la deuxième chanson, le saphir aura parcouru un angle de $\frac{2 \times 300}{300} \times 2\pi=4\pi$ . Il se trouvera donc sur le demi-axe négatif.

EXERCICE 10 :

1. La fonction cos est paire et $2\pi$ -périodique, donc la fonction f est également paire et $2\pi$ -périodique. Graphiquement, cela signifie que la courbe représentative de f est symétrique par rapport à l’axe des ordonnées et qu’elle se répète identiquement tous les $2\pi$ .

2. Comme f est $2\pi$ -périodique, il suffit d’étudier la fonction sur un intervalle de longueur $2\pi$ .

Le plus petit intervalle possible est donc $[-\pi;\pi]$ .

3. a) La fonction f’ est définie et dérivable sur tout $\mathbb{R}$ , sauf en les points où (ce qui n’a pas de sens).

Sur les autres points, on a

$f'(x)=\frac{-sin(x)(3+sin^2(x))-cos(x)2sin(x)}{(3+sin^2(x))^2}\\\\=\frac{-sin(x)(3+sin^2(x))-2cos(x)sin(x)}{(3+sin^2(x))^2}\\\\=-\frac{sin(x)(sin^2(x)+2)}{(3+sin^2(x))^2}$ .

Comme $sin^2(x)\geq\, 0$ , on a $f'(x)\leq\, 0$ si $sin(x) \geq\, 0$ et $f'(x)\geq\, 0$ si $sin(x) \leq\, 0$ .

b) Les extrema locaux de f sont les points où ou n’est pas dérivable.

Les points où f est pas dérivable sont les points où , qui n’existent pas. Donc les seuls points où f'(x)=0 sont les points où sin(x)=0, c’est-à-dire les multiples entiers de \pi.

c) Sur l’intervalle $[-\pi;\pi]$ , f est décroissante sur $[-\pi;0]$ et croissante sur $[0;\pi]$ .

Le minimum de f est donc atteint en $x=\pi$ , où $f(\pi)=-\frac{1}{3}$ , et le maximum est atteint en x=0, où .

Pour tracer la courbe de f sur $[-\pi;3\pi]$ , on peut se baser sur la périodicité de f : f est $2\pi$ -périodique donc il suffit de tracer la courbe sur un intervalle de longueur $2\pi$ et de la répéter ensuite identiquement sur chaque intervalle de même longueur.

On peut donc tracer la courbe de f sur $[0,2\pi]$ et ensuite représenter cette courbe sur chaque intervalle $[2k\pi ; (2k+2)\pi]$ en la décalant horizontalement de $2k\pi$ .

EXERCICE 12 :

1. La fonction cos est paire, donc la fonction f est également paire et $2\pi$ -périodique.

Graphiquement, cela signifie que la courbe représentative de f est symétrique par rapport à l’axe des ordonnées et qu’elle se répète identiquement tous les $2\pi$ .

2. La fonction f’ est définie et dérivable sur tout $\mathbb{R}$ .

Sur cet intervalle, f’ est positive si , c’est-à-dire si $x\in]\pi,2\pi[$ , et négative si , c’est-à-dire si $x\in ]0,\pi [$ .

Donc f est croissante sur $[0,\pi]$ et décroissante sur $[\pi,2\pi]$ .

3. Sur l’intervalle $[0,2\pi]$ , f est décroissante sur $[0,\pi]$ et croissante sur $[\pi,2\pi]$ . Le minimum de f est donc atteint en $x=\pi$ , où $f(\pi)=-\frac{1}{3}$ , et le maximum est atteint en x=0 et en $x=2\pi$ , où $f(0)=f(2\pi)=-1$ .

Ensuite, on peut dresser le tableau de variations de f sur l’intervalle $[-\pi;\frac{3}{\pi}]$ en répétant le tableau sur chaque intervalle $[2k\pi ; (2k+2)\pi]$ et en décalant horizontalement en cela pour chaque table.

EXERCICE 13 :

1. Puisque $-1\leq\, cos(x)\leq\, 1$ pour tout x, on a $-1\leq\, -x\leq\, 1$ , donc les solutions de l’équation sont dans l’intervalle [-1,1].

2. La fonction f est définie et dérivable sur [-1,1], donc elle est continue sur cet intervalle.

Puisque et , la courbe de f rencontre l’axe des abscisses au moins une fois dans l’intervalle [-1,1] .

On peut conjecturer que l’équation cos(x)=-x admet une unique solution dans cet intervalle, qui correspond à l’abscisse de l’intersection de la courbe de f avec l’axe des abscisses.

b) f'(x)=-sin(x)+1, donc f'(x) est positive si sin(x)<1, c’est-à-dire si $x\in ]-\frac{\pi}{2},\frac{\pi}{2}[$ , et négative si , c’est-à-dire si $x\in ]\frac{\pi}{2},\frac{3\pi}{2}[$ .

Donc f est croissante sur [-1,0] et décroissante sur [0,1].

c) En partant du tableau de variations de , on peut en déduire le tableau de variations de f sur [-1,1]. Puisque la fonction est croissante sur [-1,0] et décroissante sur [0,1], elle admet un unique zéro sur l’intervalle [0,1], correspondant donc à l’unique solution de l’équation dans l’intervalle [-1,1].

d) A l’aide d’une calculatrice, on obtient une valeur approchée de la solution de l’équation dans l’intervalle [-1,1] : $x \approx 0,7391$ .

EXERCICE 14 :

1. La lentille parcourt un angle de 360° en 5 secondes, donc elle parcourt un angle de $\frac{360^{\circ}}{5}=72^{\circ}$ en 1 seconde.

2. L’aire balayée par la lentille en 1 seconde est proportionnelle à l’angle parcouru en 1 seconde, donc elle vaut $\frac{72}{360}\cdot \pi (45\text{ km})^2 \approx 29,9\text{ km}^2$ .

EXERCICE 15 :

1. La fonction cos est paire, donc pour tout réel x, on a . La fonction f_m est donc paire.

Graphiquement, cela signifie que la courbe représentative de f_m est symétrique par rapport à l’axe des ordonnées.

2. Pour tout réel x, on a $f_m(x+\frac{2\pi}{m})=cos(m(x+\frac{2\pi}{m}))=cos(mx+2\pi)=cos(mx)=f_m(x)$ .

La fonction f_m est donc périodique de période $\frac{2\pi}{m}$ .

3. Puisque cos(x) est périodique de période $2\pi$ , la fonction cos(mx) est périodique de période $\frac{2\pi}{m}$ .

On peut donc se limiter à étudier f_m sur l’intervalle $[0,\frac{2\pi}{m}]$ , c’est-à-dire sur l’intervalle $[0,\frac{\pi}{m}]$ si on se restreint aux valeurs positives de x.

4. a) La fonction f'_m est définie et dérivable sur tout $\mathbb{R}$ , donc elle est continue sur tout $\mathbb{R}$ .

Puisque le sin est positif sur $[0,\frac{\pi}{m}]$ , on a $f'_m(x)=-msin(mx)\leq\, 0$ sur cet intervalle.

b) D’après le tableau de variations de f'_m , la fonction f_m est décroissante sur $[0,\frac{\pi}{m}]$ .

c) Si admet un maximum en 0 et une valeur minimale en $\frac{\pi}{m}$ , qui sont respectivement et $f_m(\frac{\pi}{m})=-1$ .

Par ailleurs, si on considère la périodicité de f_m de période $\frac{2\pi}{m}$ , on peut recopier le tableau de variation sur l’intervalle $[0,\frac{\pi}{m}]$ sur chaque intervalle de la forme $[\frac{2k\pi}{m}, \frac{(2k+1)\pi}{m}]$ , en le décalant horizontalement de $\frac{2k\pi}{m}$ .

EXERCICE 16 :

1. Le sens « O » se situe à gauche de l’axe des ordonnées.

Comme l’axe des abscisses correspond au sens « E » et que le sens « S » est dirigé vers le bas, le sens « O » est dirigé vers la gauche et en bas.

Cela correspond donc à un réel négatif qui est plus grand que $\frac{-\pi}{2}$ .

Par exemple, on peut prendre $-\frac{3\pi}{4}$ .

2. Le sens « S » est dirigé vers le bas de l’axe des ordonnées. Comme le sens « N » correspond à $\frac{\pi}{2}$ , cela correspond donc à un réel négatif.

Comme le sens « S » est à mi-chemin entre le sens « E » et le sens « O », cela correspond donc à un réel qui est le milieu entre 0 et $-\pi$ .

On a donc $-\frac{\pi}{2}$ .

3. Le sens « NE » fait un angle de $\frac{\pi}{4}$ avec l’axe des abscisses. Cela correspond donc au réel $\frac{\pi}{4}$ .

4. a) Le sens « NNE » fait un angle de $\frac{\pi}{8}$ avec l’axe des abscisses. Cela correspond donc au réel $\frac{\pi}{8}$ .

b) Par symétrie, le sens « SSE » correspond à un angle de $\frac{\pi}{8}$ avec l’axe des abscisses, donc cela correspond au réel – $\frac{\pi}{8}$ .

c) Par symétrie, le sens « NNO » correspond à un angle de $\frac{\pi}{4}$ avec l’axe des abscisses mais du côté gauche de l’axe des ordonnées (puisque c’est le symétrique du sens « NE » par rapport à l’axe des ordonnées).

Cela correspond donc à l’opposé du réel $\frac{\pi}{4}$ , c’est-à-dire $-\frac{\pi}{4}$ .

EXERCICE 17 :
$A=cos(\frac{\pi}{4})+cos(\frac{3\pi}{4})=\frac{\sqrt{2}}{2}-\frac{\sqrt{2}}{2}=0$
$B=sin(\frac{\pi}{3})-cos(\frac{\pi}{4})+sin(\frac{5\pi}{3})=\frac{\sqrt{3}}{2}-\frac{\sqrt{2}}{2}-\frac{\sqrt{3}}{2}=-\sqrt{2}$
$C=cos^2(\frac{\pi}{2})-sin^2(\frac{\pi}{2})=0-1=-1$

EXERCICE 18 :
$D=-cos(\frac{7\pi}{3})+cos(\frac{41\pi}{3})=-\frac{1}{2}-\frac{1}{2}=-1$
$B=sin(-\frac{87\pi}{4})+sin(-\frac{21\pi}{6})=-\frac{\sqrt{2}}{2}-\frac{1}{2}$

EXERCICE 19 :
Désolé, il n’y a pas de données à partir desquelles résoudre un exercice.

EXERCICE 20 :
1. En utilisant les coordonnées des points M et N, on obtient un système d’équations à deux inconnues a et b :

$a \times cos(-\frac{\pi}{2})+b \times sin(-\frac{\pi}{2})=2$
$a \times cos(\frac{\pi}{4})+b \times sin(\frac{\pi}{4})=\sqrt{2}$

En résolvant ce système, on trouve $a=\sqrt{2}$ et $b=2\sqrt{2}$ .

2. En utilisant les valeurs de a et b obtenues, on peut écrire :

$f(x)=\sqrt{2}cos(x)+2\sqrt{2}sin(x)$

3. Pour montrer que f est $2\pi$ -périodique, on peut calculer $f(x+2\pi)$ et vérifier qu’on obtient la même expression que f(x) .

En effectuant les calculs, on obtient :

$f(x+2\pi)=\sqrt{2}cos(x+2\pi)+2\sqrt{2}sin(x+2\pi)$
$= \sqrt{2}cos(x)+2\sqrt{2}sin(x)$
= f(x)

Ceci signifie que si on trace la courbe représentative de f sur un intervalle $[a, a+2\pi]$ , on pourra la décaler de 2\pi pour obtenir la courbe sur l’intervalle $[a+2\pi, a+4\pi]$ , et ainsi de suite.

4. Pour déterminer si f est paire ou impaire, il faut vérifier si (cas d’une fonction paire) ou (cas d’une fonction impaire).

En remplaçant x par -x dans l’expression de f, on obtient :

$f(-x)=\sqrt{2}cos(-x)+2\sqrt{2}sin(-x)$
$= \sqrt{2}cos(x)-2\sqrt{2}sin(x)$

On constate que f(-x) est différent de f(x) et de -f(x) , donc f n’est ni paire ni impaire.

Voir Corrigés 11 à 20...

Télécharger puis imprimer cette fiche en PDF.

Télécharger ou imprimer cette fiche «corrigé des exercices sur la trigonométrie en 1ère.» au format PDF afin de pouvoir travailler en totale autonomie.