Cosinus : exercices de maths en 4ème corrigés en PDF.

Le cosinus d’un angle aigu avec des exercices de maths en 4ème corrigés. En effet, ce dernier devra connaître sa formule du cosinus d’un angle dans un triangle rectangle. De plus, il vous permet de développer des compétences en géométrie et en calcul en déterminant soit une longueur dans un triangle rectangle ou la mesure d’un des angles aigus. Avec ce cosinus, vous allez découvrir une nouvelle méthode de résolution des problèmes.
En outre, la trigonométrie étudie les triangles et les relations entre les longueurs de leurs côtés et les angles aux sommets.
Ce chapitre nous donne un nouvel outil de travail dans le triangle rectangle et le corrigé des énoncés permet à l’élève de repérer ses erreurs afin de progresser et développer des compétences sur le cosinus en quatrième sur des supports similaires à votre manuel scolaire.

Exercice n° 1 :

1) Construire un triangle ABC rectangle en A sachant que :

AB = 6 cm et $\widehat{ABC}$ = 35°.

2) Calculer la longueur BC et la longueur AC ; on donnera les résultats au millimètre le plus proche.

Angle	Cosinus
35°	0,819

Exercice n° 2 :

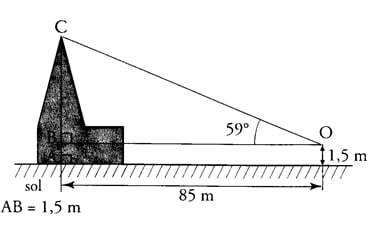
On veut mesurer la hauteur d’une cathédrale. Grâce à un instrument de mesure placé en O, à 1,5 m du sol et à 85 m de la cathédrale, on mesure l’angle $\widehat{COB}$ et on trouve 59°.

1) Déterminer la longueur CB au dixième de mètre le plus proche.

2) En déduire la hauteur de la cathédrale que l’on arrondira au mètre le plus proche.

Exercice n° 3 :

ABC est un triangle rectangle en A.

On donne AB = 5 cm et $\widehat{ABC}$ = 35°.

1) Construire la figure en vraie grandeur.

2) Déterminer la longueur AC, arrondie au dixième de centimètre.

Exercice n° 4 :

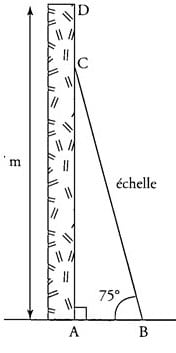
Une échelle de 6 mètres est appuyée contre un mur vertical de 7 mètres de haut. Par mesure de sécurité, on estime que l’angle que fait l’échelle avec le sol doit être de 75° (voir schéma ci-dessous).

l) Calculer la distance AB entre le pied de l’échelle et le mur. (On donnera le résultat arrondi au centimètre.)

2) A quelle distance CD du sommet du mur se trouve le haut de l’échelle ? (On donnera le résultat arrondi au centimètre.)

Exercice n° 5 :

Tracer un cercle C de centre O et de rayon 4 cm. Tracer [AB], un diamètre de C.

Placer un point E sur le cercle C tel que : $\widehat{BAE}$ = 40°.

1) Montrer que le triangle ABE est rectangle.

Calculer la valeur exacte de BE puis son arrondi au millimètre.

2) Placer le point D symétrique de B par rapport à E.

Démontrer que les droites (AD) et (OE) sont parallèles.

3) Quelle est la nature du triangle ABD ? Justifier.

Exercice n° 6 :

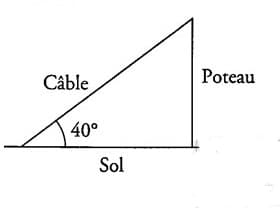
Un câble de 20 m de long est tendu entre le sommet d’un poteau vertical et le sol horizontal. Il forme un angle de 40° avec le sol (voir schéma).

1. Calculer la hauteur du poteau.

2. Représenter la situation par une figure à l’échelle $\frac{1}{200}$ (les données de la situation doivent être placées sur la figure).

Exercice n° 7 :

ABCD désigne un rectangle tel que AB = 7,2 cm et BC = 5,4 cm.

1) Dessiner en grandeur réelle ce rectangle et sa diagonale [AC].

2) Calculer la mesure arrondie au degré de l’angle $\widehat{ACD}$ .

3) Démontrer que les angles $\widehat{ACD}$ et $\widehat{CAB}$ sont égaux.

4) La médiatrice du segment [AC] coupe la droite (AB) en E. Placer le point E et montrer que le triangle ACE est isocèle.

5) En déduire une valeur approchée de la mesure de l’angle .

4.2/5 - (11 votes)

Télécharger puis imprimer cette fiche en PDF.

Télécharger ou imprimer cette fiche «cosinus : exercices de maths en 4ème corrigés en PDF.» au format PDF afin de pouvoir travailler en totale autonomie.

D'autres cours et exercices à consulter

Mathématiques Web c'est 2 268 237 fiches de cours et d'exercices téléchargées.