Corrigé des exercices sur le théorème de Pythagore en 4ème.

Le théorème de Pythagore en 4ème est à comprendre pour une bonne pratique. De plus, ce théorème de Pythagore reviendra souvent tout au long de l’année scolaire en 4ème .

Exercice 1 :

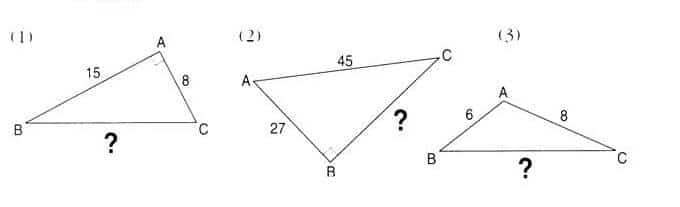
1) Dans chacun des cas suivants, calculer, si possible, la longueur BC.

Toutes les longueurs sont données en centimètres.

Les trangles ABC et ARC sont rectangles donc d’après la partie directe du théorème de Pythagore,

nous avons les égalités suivantes :

$BC^2=AB^2+AC^2\\BC^2=15^2+8^2=225+64=289$

donc $BC=\sqrt{289}=17$ .

$AC^2=AR^2+RC^2\\45^2=27^2+RC^2\\2025=729+RC^2\\RC^2=2025-729=1296$

donc $RC=\sqrt{1296}=36$ .

Pour le troisième triangle, il n’est pas rectangle donc on ne peut pas appliquer le théorème

de Pythagore et nous ne disposons pas suffisament de données pour résoudre ce problème.

2) RST est un triangle rectangle en R tel que RS = 2 cm et RT = 1 cm. Calculer ST.

Le résultat en centimètres est-il un nombre entier ? Sinon, trouver un arrondi de ST au dixième de centimètre près.

Le triangle RST est rectangle en R donc d’après la partie directe du théorème de Pythagore,

nous avons l’égalité suivante :

$ST^2=SR^2+RT^2\\ST^2=2^2+1^2=5$

donc $ST=\sqrt{5}$ cm.

Exercice 2 :

Qui a raison ?

Faux, cela dépend du nom du sommet de l’angle droit.

Exercice 3 : La surprise finale.

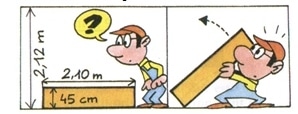
Le plafond est-il assez haut pour que Monsieur Bricoltou mette en place son meuble ?

La longueur la plus élevée est la diagonale du meuble.

Le meuble possède des angles droits donc on peut appliquer la partie directe du théorème

de Pythagore.

45 cm = 0,45 m.

La diagonale mesure $\sqrt{2,1^2+0,45^2}\simeq 2,15$ m.

Conclusion : le plafond n’est pas assez haut pour que Monsieur Bricoltou mette en place son meuble.

Exercice 4 :

Une chèvre C est attachée à un piquet P planté au coin d’un pré carré de 15 m de côté.

Quelle doit être, approximativement, la longueur de la corde pour que la chèvre puisse brouter tout le pré?

La longueur la plus longue est celle de la diagonale.

Un carré possède des angles droits donc on peut appliquer la partie directe du théorème de Pythagore.

La longueur de la diagonale vaut $\sqrt{15^2+15^2}=\sqrt{500}\simeq 22,4\,m$ .

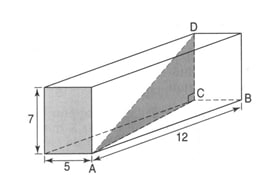
Exercice 5 : le parallélépipède rectangle.

Combien mesure à 0,01 près, la diagonale du parallélépipède rectangle?

Dans le triangle ABC rectangle en B, d’après la partie directe du théorème de Pythagore,

nous avons l’égalité suivante :

$AC=\sqrt{169}=13$

Dans le triangle ACD, rectangle en C, d’après la partie directe du théorème de Pythagore, nous avons l’égalité suivante :

donc $AD=\sqrt{218}\simeq 14,77$

Exercice 6 :

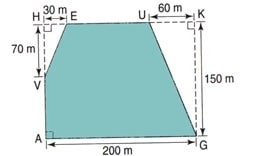
Monsieur Crésus possède un terrain VAGUE qu’il veut clôturer.

Calculer le périmètre du terrain VAGUE.

$VA=150-70=80\,m$

$EU=200-30-60=110\,m$

Il nous reste à calculer les longueurs VE et UG.

Dans le triangle VHE rectangle en H , d’après la partie directe du théorème de Pythagore, nous avons l’égalité suivante :

$VE^2=VH^2+HE^2\\VE^2=70^2+30^2=5800$ donc $VE=\sqrt{5800}\simeq 76,16\,m$ .

Dans le triangle UKG rectangle enK , d’après la partie directe du théorème de Pythagore, nous avons l’égalité suivante :

$UG^2=UK^2+KG^2\\UG^2=60^2+150^2=26\,100$

donc $UG=\sqrt{26\,100}\simeq 161,55\,m$

Périmètre du terrain VAGUE :

$P_{vague}=AG+GU+UE+EV+VA$

$P_{vague} \simeq 200+161,55+110+76,16+80\simeq 627,71\,m$

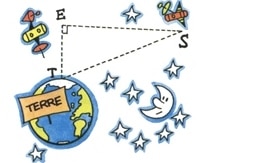
Exercice 7 :

Quelle distance sépare les deux satellites E et S, sachant que l’angle $\widehat{TES}$ est droit et qu’un signal radio met $\frac{1}{60}$ de seconde de S à T et $\frac{1}{100}$ de seconde de E à T ?

(Vitesse du signal radio : 300 000 km/s.)

Nous sommes dans une situation de proportionnalité :

$300\,000\,kmrightarrow 1s\\STrightarrow \frac{1}{60}s$ donc $ST=300000\times \frac{1}{60}=5\,000\,km$ .

$300\,000\,kmrightarrow 1s\\ETrightarrow \frac{1}{100}s$ donc $ET=300\,000\times \frac{1}{100}=3\,000\,km$ .

Le triangle TES est rectangle en S donc d’après la partie directe du théorème de Pythagore,

nous avons l’égalité suivante :

$ES^2=5000^2-3000^2=16\,000\,000$

$ES=\sqrt{16000000}=4\,000\,km$

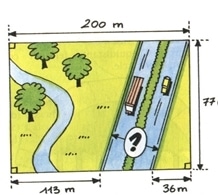
Exercice 8 :

Quelle est la largeur de l’autoroute ?

(Non, ce n’est pas 51 mètres !)

Le triangle situé en bas à droite est un triangle rectangle donc nous pouvons appliquer

la partie directe du théorème de Pythagore :

La longueur de l’autoroute vaut :

$\sqrt{36^2+77^2}=\sqrt{7225}=85\,m$

200-113-36= 51 m.

L’aire du trapèze est : $A_{trapeze}=\frac{(B+b)\times h}{2}=\frac{((200-51)+113)\times 77}{2}=10\,087\,m^2$

L’aire du triangle rectangle est : $A_{triangle-rectangle}=\frac{36\times 77}{2}=1386\,m^2$

L’aire de l’autoroute correspond à l’aire du grand rectangle privée de l’aire du trapèze et

du triangle rectangle.

$A_{autoroute}=200\times 77-10087-1386=3927\,m^2$

Or, l’autoroute est un parallélogramme dont l’aire est base x largeur de l’autoroute.

Donc $85\times L=3927$ ainsi $L=\frac{3927}{85}=46,2\,m$ .

Conclusion : la largeur de l’autoroute est de 46,2 mètres.

Voter pour post

Télécharger puis imprimer cette fiche en PDF.

Télécharger ou imprimer cette fiche «corrigé des exercices sur le théorème de Pythagore en 4ème.» au format PDF afin de pouvoir travailler en totale autonomie.

D'autres cours et exercices à consulter

Mathématiques Web c'est 2 268 364 fiches de cours et d'exercices téléchargées.