Calcul littéral maths : exercices en 4ème corrigés en PDF.

Le calcul littéral et la double distributivité à travers des exercices de maths en 4ème corrigés vous sera très avantageux. Ainsi, l’élève devra être capable de simplifier et réduire une expression algébrique et connaître les règles de simplification. Il doit aussi développer une expression littérale en utilisant les propriétés de la simple et de la double distributivité. De plus, il devra aussi développer des compétences en calcul littéral à travers des exercices qui possède leur correction afin de progresser avec ces énoncés.

Exercice 1 :

Ecrire de la façon la plus simple les expressions suivantes :

$a. 2\times \,3x\\ b. -3\times \,7x \\ c. 2\times \,(5x) \\ d. x\times \,7 \\ e. x\times \,(-3) \\ f. 3x\times \,(2x) \\ g. -7x\times \,(2x) \\ h. -6x\times \,(-4x)$

Exercice 2 :

Développer et réduire les expressions suivantes :

f. (3a – 4)(4a – 11)

k. (- a + 5b)(4b + 3a)

Exercice 3 :

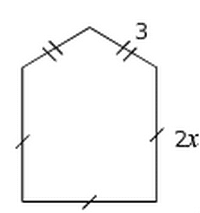
Déterminer le périmètre de la figure ci-dessous en fonction de x.

Exercice 4 :

En utilisant la propriété de la double distributivité, développer et réduire les expressions littérales suivantes :

$B = ( x + 7 ) \times ( x + 2 )$ C = ( x + 2 ) ( x – 5 )

D = ( x + 3 ) ( x – 6 ) E = ( x + 6 ) ( x – 8 ) F = ( x – 3 ) ( x + 4 )

G = ( x – 7 ) ( x – 4 ) H = ( x – 1 ) ( x + 7 ) I = ( 2 x + 7 ) ( 3 x + 8 )

Exercice 5 :

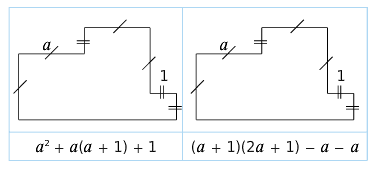
On souhaite exprimer l’aire de la figure ci-dessous, en fonction de a.

1.Voici deux propositions. Indiquer le découpage utilisé pour obtenir l’expression donnée.

2.Proposer une autre expression.

3.Montrer que les différentes expressions peuvent s’écrire 2a²+a+1.

Exercice 6 :

Voici deux programmes de calcul.

a. On choisit le nombre 2.
Calculer le nombre obtenu avec le programme A, puis avec le programme B.
b. Serge affirme : « J’ai choisi un nombre et les deux programmes ont donné le même résultat ».
Déterminer le nombre choisi par Serge en résolvant une équation.

Exercice 7 :

Dans un magasin :
• Jordan achète 4 BD au même prix et un manga à 8 €.

• Piala achète 2 de ces BD et un dictionnaire 45 €.
A la caisse, ils paient la même somme.
On se propose de déterminer le prix p, en euros, de chaque BD.

1. Exprimer en fonction de p, le montant :
a. de la dépense de Jordan,
b. de la dépense de Piala.
2. Déterminer p en résolvant une équation.

Exercice 8 :

A vélo, Dylan a fait trois tours du lac puis il a parcouru 7 km en forêt.

Loris n’a fait qu’un seul tour du lac mais il a parcouru 16 km en forêt.
A leur arrivée, ils constatent qu’ils ont parcouru la même distance totale.
Voici un schéma qui représente la situation.

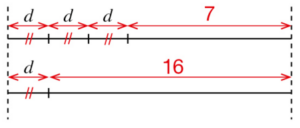
a. Que représente l’inconnue d sur ce schéma ?
b. Calculer mentalement la valeur de d. Interpréter ce résultat.

Exercice 9 :

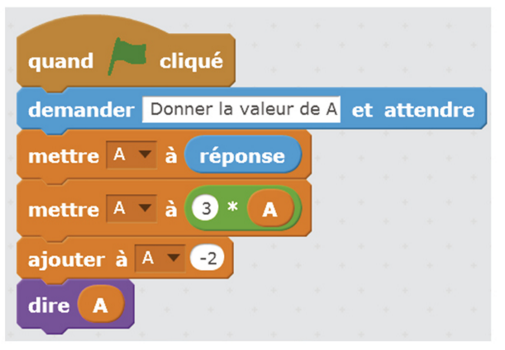
Voici un programme écrit avec le langage Scratch.

a. Que permet de faire ce programme ?
b. Quelle valeur annonce le lutin la fin du programme si l’on saisit 5 au début ?
c. Quelle valeur a-t-on saisie au début du programme si le lutin annonce 4 à la fin ?

Exercice 10 :

Dans chaque cas, citer l’inconnue et dire s’il s’agit ou non d’une équation du premier degré.
$a. \,-9a=4a+13$
$b.\,2x^2-3=7x+3$
$c.\, 8-6y=4+2y$
$d.\, t(t+ 1) = 2t$

Exercice 11 :

Voici un programme de calcul.

On note x le nombre choisi au départ.
1.a. Exprimer en fonction de x le nombre N obtenu avec ce programme.
b. Développer et réduire cette expression.
c. Factoriser cette expression.
2. Calculer N pour : x = 0 puis x = 2.

Exercice 12 :

Voici un programme de calcul.

On note le nombre choisi au départ.
1.a. Exprimer en fonction de le nombre obtenu avec ce programme.
b. Réduire cette expression.
c. Factoriser cette expression.

2. Calculer pour : puis .

Exercice 13 :

On considère ce rectangle dont les côtés ont des longueurs variables exprimées dans la même unité.
x désigne un nombre positif.

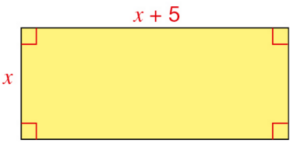
a. Que désigne pour ce rectangle chacune de ces expressions ?

Répondre éventuellement « rien ».

$A=x\times x+5\\B=2x+2(x+5)\\C=x(x+5)\\D=2(x+x+5)$
b. Calculer le périmètre de ce rectangle pour x = 3, puis pour x = 7,5.
c. Calculer l’aire de ce rectangle pour x = 4, puis pour x = 10.

Exercice 14 :

Dans chaque cas, dire si l’affirmation est vraie ou fausse. Justifier.
a. « Pour , A est égal à 30. »

b. « Pour , B est égal à 18. »

c. «Pour , C est égal à 1.»

Exercice 15 :

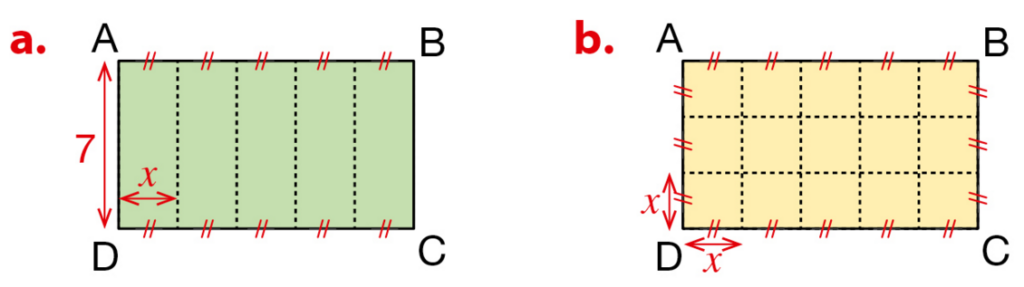
1. Dans chaque cas, exprimer l’aire du rectangle ABCD en fonction de x.

2. Dans chaque cas, calculer l’aire du rectangle ABCD pour x = 6.

Exercice 16 :

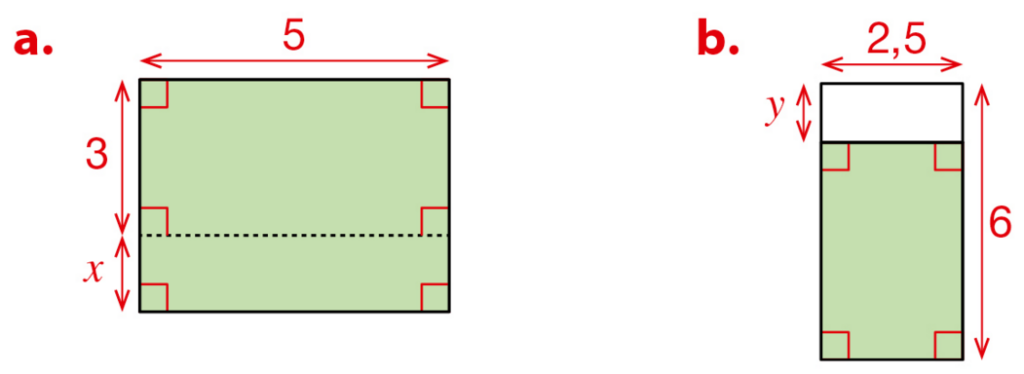
Dans chaque cas, donner l’aire du rectangle coloré en vert sous forme d’un produit et sous forme
d’une somme algébrique.

Exercice 17 :

Sur cette figure, le côté de ce carré a une longueur x, en cm, variable avec x < 6.

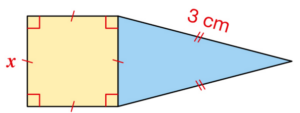
a. Que désigne pour cette figure chacune de ces expressions ?

b. Tester l’égalité B = C pour :
.

Exercice 18 :

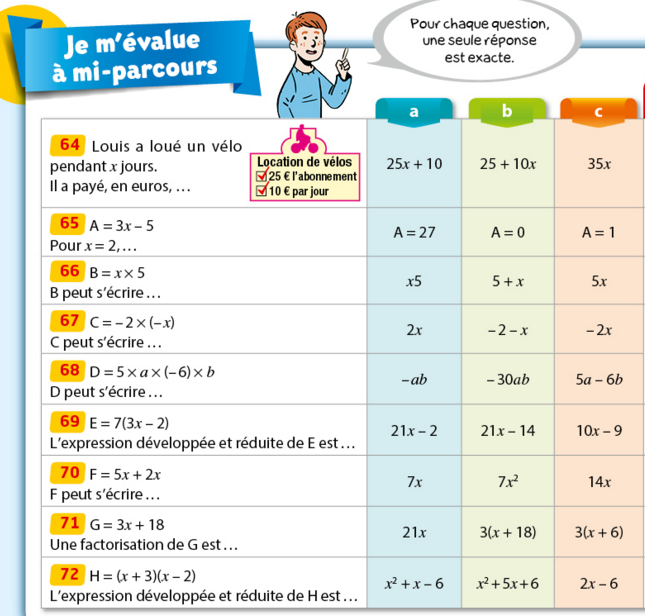
Effectuer ce QCM sur le calcul littéral.

3.5/5 - (24 votes)

Télécharger puis imprimer cette fiche en PDF.

Télécharger ou imprimer cette fiche «calcul littéral : exercices de maths en 4ème corrigés en PDF.» au format PDF afin de pouvoir travailler en totale autonomie.

D'autres cours et exercices à consulter

Mathématiques Web c'est 2 268 192 fiches de cours et d'exercices téléchargées.