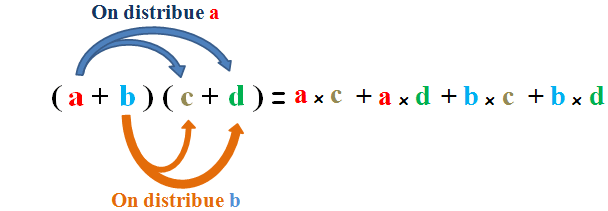Calcul littéral : cours de maths en 4ème à télécharger en PDF.

Sommaire de cette fiche

Le calcul littéral avec un cours de maths en 4ème qui est essentiel pour l’élève. Dans cette leçon sur le calcul algébrique, l’élève devra être capable d’utiliser les propriétés de la simple et de la double distributivité. Il devra développer et réduire une expression littérale et substituer une valeur de la variable.

Nous terminerons ce cours sur le calcul littéral avec la résolution de problèmes issues de la géométrie ou de la vie courante en quatrième.

I. Expression littérale

Définition :

On appelle expression littérale (ou expression algébrique) toute expression contenant une ou plusieurs lettres. Ces lettres désignent des nombres.

Exemples :

L’aire d’un carré de côté c s’exprime avec l’expression littérale $A=c\times c=c^2$ .
Un rectangle de longueur L et de largeur l a un périmètre qui s’exprime avec l’expression littérale $P=2(L+l)=2\times L+2\times l$ .

Règle de simplification :

Dans une expression littérale, nous ne noterons plus un signe x entre deux lettres, entre un nombre et une lettre, ou encore, précédé d’une parenthèse.

Exemple :

Pour un rectangle de longueur L et de largeur l , son périmètre vaut $P=2(L+l)=2\times L+2\times l=2L+2l$ .
Un cercle de rayon R a pour périmètre $P=2\pi R$ et pour aire $A=\pi R^2$ .

Remarque :

On peut simplifier $1\times x$ en et $0\times y$ en .
L’expression $3\times (p+2)$ peut s’écrire .
Attention : on ne peut pas supprimer le signe x entre deux nombres $3\times 5\neq 35$ .

Définition (puissances) :

On considère un nombre relatif a.

$a^2=a\times a$ et se lit a au carré.

$a^3=a\times a\times a$ et se lit a au cube.

Exemple :

Aire d’un carré de côté a est $A=a\times a=a^2$ .

Le volume d’un cube de côté a est $V=a\times a\times a=a^3$

II. Evaluer une expression littérale

Propriété :

Afin d’évaluer une expression littérale, on substitue (remplace) la lettre par sa valeur et nous calculons la valeur de l’expression numérique.

Exemple :

Considérons l’expression littérale .

Si x=3 alors $A=7x+1=7\times 3+1=21+1=22$
Si x = -2 alors $A=7x+1=7\times (-3)+1=-14+1=-13$

On dit que l’on substitue (remplace) la valeur de x.

On passe, ainsi, du calcul littéral au calcul numérique.

III. La simple distributivité du calcul littéral

Définition :

Développer une expression littérale, c’est l’écrire comme somme de termes.

Exemple :

est une forme développée.

Définition :

Factoriser une expression littérale, c’est l’écrire comme produit de facteurs.

Exemple :

sont des formes factorisées.

Définition :

Réduire une expression littérale, c’est regrouper tous les termes de même nature.

Exemples :

Réduire les expressions suivantes :

Propriété :

Soient k, a et b trois nombres relatifs :

Exemple :

En utilisant la simple distributivité, développer les expressions littérales suivantes :

$A=5(x+2)=5\times x+5\times 2=5x+10\\B=2(y-4)=2x-8\\C=5(2p-3)=5\times 2p-5\times 3=10p-15\\D=4(r-1)+4r+9=4r-4+4r+9=8r+5$

IV. La double distributivité du calcul littéral

Propriété : la double distributivité.

On considère quatre nombres relatifs a, b, c et d.

Exemples :

Développer et réduire les expressions suivantes :

4.1/5 - (7 votes)

Télécharger puis imprimer cette fiche en PDF.

Télécharger ou imprimer cette fiche «calcul littéral : cours de maths en 4ème en PDF.» au format PDF afin de pouvoir travailler en totale autonomie.

D'autres cours et exercices à consulter

Mathématiques Web c'est 2 267 942 fiches de cours et d'exercices téléchargées.

I. Expression littérale

II. Evaluer une expression littérale

III. La simple distributivité du calcul littéral

IV. La double distributivité du calcul littéral

Télécharger puis imprimer cette fiche en PDF.

D'autres cours et exercices à consulter

Cours de quatrième

Exercices de quatrième

Nos applications