Corrigé des exercices sur le second degré en 1ère.

EXERCICE 1 :

1)a) En utilisant la formule du discriminant, on a :

$\Delta=1^2-4\times 2\times 3=-23$

Comme $\Delta<0$ , l’équation n’a pas de solution réelle.

b) En utilisant la formule du discriminant, on a :

$\Delta=6^2-4\times 9\times 1=0$

Comme $\Delta=0$ , l’équation a une solution réelle unique donnée par $x=\frac{-6}{2\times 9}=-\frac{1}{3}$ .

c) En factorisant, on obtient : .

Les solutions de l’équation sont donc -1 et 2.

2) En utilisant la formule du discriminant, on a : $\Delta=(-21)^2-4\times 6\times 9=9$ .

Comme $\Delta>0$ , l’équation a deux solutions réelles qui sont données par :

$x_1=\frac{21+3}{12}=\frac{2}{3}$ et $x_2=\frac{21-3}{12}=1$

EXERCICE 2 :

1)a) En utilisant la formule du discriminant, on a :

$\Delta=2^2-4\times (-1)\times (-3)=8$

Comme $\Delta>0$ , la fonction a deux racines réelles données par :

$x_1=\frac{-2+\sqrt{8}}{-2}=1+\sqrt{2}$ et $x_2=\frac{-2-\sqrt{8}}{-2}=1-\sqrt{2}$

b) En utilisant la formule du discriminant, on a :

$\Delta=1^2-4\times 1\times \frac{1}{4}=0$

Comme $\Delta=0$ , la fonction a une racine réelle double donnée par :

$x=\frac{-1}{2}$

c) En utilisant la formule du discriminant, on a :

$\Delta=2^2-4\times 2\times (-12)=100$

Comme \Delta > 0, la fonction a deux racines réelles données par :

$x_1=\frac{-2+\sqrt{100}}{4}=\frac{1}{2}$ et $x_2=\frac{-2-\sqrt{100}}{4}=-3$ .

2) a) En utilisant la formule du discriminant, on a :

$\Delta=(-5)^2-4\times 4\times 10=-136$ .

Comme $\Delta<0$ , l’équation n’a pas de solution réelle.

b) En utilisant la formule du discriminant, on a : $\Delta=(-3)^2-4\times 3\times (-60)=849$ .

Comme $\Delta>0$ , l’équation a deux solutions réelles données par :

$x_1=\frac{3+\sqrt{849}}{6}$ et $x_2=\frac{3-\sqrt{849}}{6}$

c) En utilisant la formule du discriminant, on a :

$\Delta=(-24)^2-4\times 72\times 2=-432$

Comme $\Delta<0$ , l’équation n’a pas de solution réelle.

EXERCICE 3 :

La fonction f est un polynôme de degré 2.

Pour déterminer le nombre de racines de la fonction, on calcule le discriminant : $\Delta=(-\frac{49}{2})^2-4\times (-7)\times 14=1681$ .

Comme $\Delta>0$ , la fonction a deux racines réelles distinctes.

On vérifie que -4 est une racine en remplaçant x par -4 dans f(x) :

$f(-4)=-7\times (-4)^2-\frac{49}{2}\times (-4)+14=0$

Donc -4 est bien une racine de f.

En utilisant la somme des racines, on a :

$x_1+x_2=-\frac{b}{a}=\frac{49}{14}$

En utilisant le produit des racines, on a :

$x_1\times x_2=\frac{c}{a}=-2$ .

Les racines sont solutions de l’équations avec S la somme des deux racines et P leur produit.

En résolvant ce système, on trouve que les deux racines sont -2 et $\frac{7}{2}$ .

EXERCICE 4 :

a) La fonction f(x) est un polynôme de degré 2 car le terme de plus haut degré est .

b) La fonction g(x) n’est pas un polynôme de degré 2 car elle contient une fraction.

c) La fonction h(x) n’est pas un polynôme de degré 2 car le terme de plus haut degré est x.

EXERCICE 5 :

1) En développant l’expression, on obtient :

2) La forme canonique de f est de la forme , où est le sommet de la parabole.

Pour obtenir cette forme, on complète le carré :

Donc la forme canonique de f est , et le sommet est (4,55).

L’axe de symétrie est la droite verticale passant par le sommet.

Dans ce cas, c’est la droite x = 4.

Le signe de a est -3, donc la parabole est orientée vers le bas.

EXERCICE 6 :

a) La forme canonique de est :

Le sommet est et l’axe de symétrie est la droite x = 3.

Le signe de a est 1, donc la parabole est orientée vers le haut.

b) La forme canonique de est :

$f(x)=(x+\frac{5}{2})^2-\frac{1}{4}$

Le sommet est $(-\frac{5}{2},-\frac{1}{4})$ et l’axe de symétrie est la droite $x=-\frac{5}{2}$ .

Le signe de a est 1, donc la parabole est orientée vers le haut.

EXERCICE 7 :

a) Les coordonnées du sommet sont $(-\frac{b}{2a},-\frac{\Delta}{4a})=(-\frac{1}{2},-\frac{1}{4})$ .

L’axe de symétrie est la droite $x=-\frac{1}{2}$ .

Le signe de a est 1, donc la parabole est orientée vers le haut.

b) Les coordonnées du sommet sont $(-\frac{b}{2a},-\frac{\Delta}{4a})=(1,1)$ .

L’axe de symétrie est la droite x = 1.

Le signe de a est 2, donc la parabole est orientée vers le haut.

c) Les coordonnées du sommet sont $(-\frac{b}{2a},-\frac{\Delta}{4a})=(-1,-\frac{1}{2})$ .

L’axe de symétrie est la droite x = -1.

Le signe de a est 2, donc la parabole est orientée vers le haut.

EXERCICE 8 :

a) L’axe de symétrie est la droite $x=-\frac{b}{2a}=-\frac{1}{2}$ .

Les coordonnées du sommet sont $(\frac{1}{4},\frac{5}{8})$ .

b) L’axe de symétrie est la droite $x=-\frac{b}{2a}=\frac{1}{2}$ .

Les coordonnées du sommet sont $(\frac{5}{4},\frac{47}{8})$ .

c) L’axe de symétrie est la droite $x=-\frac{b}{2a}=-3$ .

Les coordonnées du sommet sont (-3,-6).

d) L’axe de symétrie est la droite $x=-\frac{b}{2a}=\frac{1}{2}$ .

Les coordonnées du sommet sont $(\frac{1}{2},2)$ .

EXERCICE 9 :

a) On utilise l’identité remarquable :

b) On utilise l’identité remarquable :

$f(x)=x^2-3=(x-\sqrt{3})(x+\sqrt{3})$

c) Pour factoriser , on cherche deux nombres dont la somme est $-\frac{b}{a}=\frac{4}{5}$ et le produit est $\frac{c}{a}=\frac{1}{25}$ .

Ces nombres sont $-\frac{2}{5}$ et $-\frac{1}{5}$ , donc :

$f(x)=25x^2-20x+4=25(x-\frac{2}{5})(x-\frac{1}{5})$

d) Pour factoriser 9x^2 + 24x + 16, on cherche deux nombres dont la somme est $-\frac{b}{a}=-\frac{8}{3}$ et le produit est $\frac{c}{a}=\frac{16}{9}$ .

Ces racines doubles sont $-\frac{4}{3}$ , donc :

$f(x)=9x^2+24x+16=9(x+\frac{4}{3})^2$

EXERCICE 10 :

a) Le discriminant est $\Delta=4-4\times 5=-16$ , donc l’équation n’a pas de solution réelle.

b) Le discriminant est $\Delta=1+4\times 2\times 6=49$ , donc l’équation a deux solutions réelles.

c) Le discriminant est $\Delta=4-4\times (-\frac{1}{3})\times 2=\frac{8}{3}$ , donc l’équation a deux solutions réelles.

d) Le discriminant est $\Delta=2^2-4\times (-1)\times 3=16$ , donc l’équation a deux solutions réelles.

EXERCICE 11 :

a) On peut factoriser le trinôme par 3 : .

Donc les solutions sont x = 4 et x = -1.

b) Le discriminant est $\Delta=5^2-4\times 2\times 7=-31$ , donc l’équation n’a pas de solution réelle.

c) Le discriminant est $\Delta=(-2)^2-4\times 2\times (-\frac{1}{2})=6$ , donc l’équation a deux solutions réelles.

EXERCICE 12 :

a) On factorise le trinôme : .

Les solutions sont donc : x < 0 ou x > 2.

b) Le trinôme est déjà factorisé : $(x-9)(x+9)\leq\,0$ .

Les solutions sont $x\leq\,-9$ ou $x\geq\,9$ .

c) On trouve les racines du trinôme comme ceci : $(x-\frac{3}{2})(x+2.8)=0$ .

Les racines sont donc $x=\frac{3}{2}$ et x=-2.8 .

Il faut maintenant déterminer le signe de la fonction pour les intervalles suivants : $]-\infty,-2.8[,]-2.8,\frac{3}{2}[$ et $]\frac{3}{2},+\infty[$ .

On peut utiliser le test de signe ou la forme canonique de la fonction.

La forme canonique est $f(x)=(x-\frac{3}{2})(x+2.8)$ , donc on voit que la parabole est orientée vers le haut (a>0) , et que les racines divisent le plan en deux intervalles.

Donc le signe de la fonction est positif sur $(-2.8,\frac{3}{2})$ .

d) Le trinôme est déjà factorisé : .

Comme a>0 , la parabole est orientée vers le haut et n’a pas de racines réelles.

Donc la fonction est négative pour tout x réel.

EXERCICE 13 :

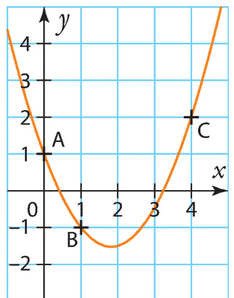
1. Le point A est sur la courbe de f, donc .

En utilisant les coordonnées du point A, on a :

On peut utiliser les deux autres points pour écrire un système d’équations.

On utilise la méthode de substitution :

On peut résoudre ce système en soustrayant l’équation du point B à l’équation du point A, ce qui élimine le terme en c :

$\frac{y_A-y_B}{x_A-x_B}=-3(x_A+x_B)+24$

On peut ensuite soustraire l’équation du point C à l’équation du point A, ce qui permet d’éliminer le terme en x_B :

$\frac{y_A-y_C}{x_A-x_C}=-3(x_A+x_C)+24$

On a ainsi deux équations linéaires à deux inconnues : et .

En les soustrayant, on trouve .

On peut ensuite utiliser cette équation pour exprimer x_B en fonction de x_C et simplifier les deux autres équations pour trouver les valeurs de a, b et c :

En substituant ces expressions dans les équations obtenues plus tôt, on trouve que et c=-41 .

Donc l’expression de f est .

EXERCICE 14 :

a) Le discriminant est $\Delta=4-4\times 5=-16$ , donc l’équation n’a pas de solution réelle.

b) Le discriminant est $\Delta=1+4\times 2\times 6=49$ , donc l’équation a deux solutions réelles.

c) Le discriminant est $\Delta=4-4\times (-\frac{1}{3})\times 2=\frac{8}{3}$ , donc l’équation a deux solutions réelles.

d) Le discriminant est $\Delta=2^2-4\times (-1)\times 3=16$ , donc l’équation a deux solutions réelles.

EXERCICE 15 :

a) Le discriminant est $\Delta=3^2-4\times 3\times 2=-3$ , donc l’équation n’a pas de solution réelle.

b) Le discriminant est $\Delta=(-5)^2-4\times 2\times 7=-31$ , donc l’équation n’a pas de solution réelle.

c) Le discriminant est $\Delta=2^2-4\times (-\frac{1}{3})\times 2=\frac{8}{3}$ , donc l’équation a deux solutions réelles.

d) Le discriminant est $\Delta=7^2-4\times 2\times 11=9$ , donc l’équation a deux solutions réelles.

EXERCICE 16 :

a) Le sommet est sur l’axe des x, donc $\Delta=0$ .

b) Le sommet est en dessous de l’axe des x, donc $\Delta>0$ .

c) Le sommet est au dessus de l’axe des x, donc $\Delta<0$ .

d) Le sommet est au dessus de l’axe des x, donc $\Delta<0$ .

EXERCICE 17 :

a) On trouve les racines du trinôme : .

On peut en déduire le tableau de signes :

x | -∞ | 2 | 4 | +∞ —|—-|—|—|—-

f(x) | – | 0 | + | +

b) On trouve les racines du trinôme :

$-\frac{4}{3}(-\frac{3}{2}-x)(-\frac{3}{2}+x)$ .

On peut en déduire le tableau de signes :

x | -∞ | $-\frac{3}{2}$ | $\frac{1}{2}$ | +∞

—|—-|———–|———|—-

f(x) | + | 0 | – | – c)

On trouve les racines du trinôme :

$2(x-\frac{5}{4})(x-\frac{1}{2})$ .

On peut en déduire le tableau de signes :

x | -∞ | $\frac{1}{2}$ | $\frac{5}{4}$ | +∞

—|—-|———–|———–|—-

f(x) | – | + | – | –

EXERCICE 18 :

a) On factorise le trinôme : .

Les racines sont 0 et 2, donc il y a deux intervalles à considérer : $]-\infty;0[$ et ]0;2[ .

On peut utiliser le test de signe ou la forme canonique de la fonction pour déterminer le signe sur ces intervalles.

On trouve que la fonction est positive sur ]0;2[ et négative sur $]-\infty;0[$ et $]2;+\infty[$ .

Donc les solutions sont x<0 ou x>2 .

b) On trouve les racines du trinôme : $(x-9)(x+9)\leq\,0$ .

Les racines sont -9 et 9, donc il y a trois intervalles à considérer : $]-\infty;-9]$ , [-9,9] et $[9;+\infty[$ .

On peut utiliser le test de signe ou la forme canonique de la fonction pour déterminer le signe sur ces intervalles.

On trouve que la fonction est négative sur [-9,9] et positive sur $]-\infty;-9]$ et $[9;+\infty[$ .

Donc les solutions sont $x\leq\,-9$ ou $x\geq\,9$ .

c) On trouve les racines du trinôme :.

Les racines sont , donc il y a quatre intervalles à considérer :

$]-\infty,-2,8[,]-2,8,0[,]0,1,5[$ et $]1,5;+\infty[$ .

On peut utiliser le test de signe ou la forme canonique de la fonction pour déterminer le signe sur ces intervalles.

On trouve que la fonction est négative sur et positive sur $]-\infty,-2.8[,]0,1,5[$ et $]1,5,+\infty[$ . Donc les solutions sont x<-2.8 ou $x\in]0,1,5[$ .

d) Le trinôme est déjà factorisé : .

Comme a>0 , la parabole est orientée vers le haut et n’a pas de racines réelles.

Donc la fonction est négative pour tout x réel.

Donc la solution est l’ensemble vide.

EXERCICE 19 :

a) On commence par résoudre l’équation associée $f(x)=3x^2-4x+\frac{4}{3}=0$ .

On calcule le discriminant : $\Delta=(-4)^2-4\times 3\times \frac{4}{3}=4$ .

Le trinôme a donc deux solutions réelles.

En étudiant le signe de f(x) pour les intervalles $]-\infty,\frac{1}{2}]$ , $[\frac{1}{2},+\infty[$ , on trouve que la solution est $x\in[\frac{1}{2},1]$ .

b) On commence par résoudre l’équation associée .

On calcule le discriminant : $\Delta=(-50.5)^2-4\times 5\times 5=2470$ .

Le trinôme a donc deux solutions réelles.

En étudiant le signe de f(x) pour les intervalles $]-\infty,\frac{1}{2}[$ , $]\frac{1}{2},+\infty[$ ,

on trouve que la solution est $x\in]\frac{1}{10},\frac{1}{2}[$ .

c) La parabole est orientée vers le haut, donc f(x)>0 pour tout x.

Donc la solution est l’ensemble $\mathbb{R}$ .

d) On commence par résoudre l’équation associée .

On calcule les racines du trinôme : $x=\frac{3\pm\sqrt{39}}{4}$ .

On peut alors dresser le tableau de signes de f(x) :

x | -∞ | $\frac{3-\sqrt{39}}{4}$ | $\frac{3+\sqrt{39}}{4}$ | +∞
—|—-|———————–|—————-

EXERCICE 20 :

1. On complète le carré : .

Donc la forme canonique de f est , et le sommet est (3,-63) .

L’axe de symétrie est la droite verticale passant par le sommet.

Dans ce cas, c’est la droite x=3 .

Le signe de a est 1, donc la parabole est orientée vers le haut.

2. On peut factoriser f(x) comme suit :

a) On résout f(x)=0 en utilisant la forme factorisée :

Les solutions sont x=9 et x=-3 .

b) On résout f(x) = -27 en utilisant la forme factorisée :

On peut réécrire -27 comme $3^3\times (-1)$ , et on utilise cette astuce pour factoriser :

$(x-9)(x+3)+3^3\times (-1)=0$

En utilisant la forme canonique, on voit que le sommet de la parabole est à (9,0) , et que la distance entre le sommet et l’axe des x est de 3.

Donc les racines sont à une distance de 3 de l’axe des x, et se trouvent donc à 6 et 12 :

x=9-3=6 ou

c) On résout en utilisant la forme factorisée :

On peut réécrire comme $3^2\times (-4)$ , et on utilise cette astuce pour factoriser :

$(x-9)(x+3)+3^2\times (-4)=0$
$(x-9)^2+3^2-2\times 3^2=0$

Là encore, on retrouve une équation de la forme , donc la seule solution est x=9 .

a) On vérifie que 1 est racine en remplaçant x par 1 dans g(x) :

$g(1)=2\times 1^2-\frac{3}{2}\times 1-\frac{1}{2}=0$

Donc 1 est bien racine de g.

b) En utilisant le produit et la somme des racines, on sait que :

$x_1\times x_2=-\frac{1}{4}$ et $x_1+x_2=\frac{3}{4}$

On sait aussi que x_1 = 1. On peut utiliser ces informations pour déterminer la valeur de x_2 :

$x_1+x_2=1+x_2=\frac{3}{4}\Rightarrowx_2=-\frac{1}{4}$

Donc les racines de g sont 1 et $-\frac{1}{4}$ .

5. Pour résoudre f(x) < g(x), on peut d’abord réécrire les deux fonctions sous forme canonique :

$g(x)=2(x-\frac{1}{4})^2-\frac{1}{2}$

En soustrayant les deux fonctions, on trouve :

$f(x)-g(x)=(x-3)^2-2(x-\frac{1}{4})^2-\frac{125}{4}$

On veut maintenant trouver les valeurs x pour lesquelles , c’est-à-dire les valeurs pour lesquelles.

Voir Corrigés 11 à 20...

Télécharger puis imprimer cette fiche en PDF.

Télécharger ou imprimer cette fiche «corrigé des exercices sur les équations et inéquations du second degré en 1ère.» au format PDF afin de pouvoir travailler en totale autonomie.

Réviser les cours et exercices avec nos Q.C.M :

Q.C.M en 6ème Q.C.M en 5ème Q.C.M en 4ème Q.C.M en 3ème Q.C.M en 2de Q.C.M en 1ère Q.C.M en Terminale

D'autres ressources pour progresser en autonomie :

Chronomètre Horloge France Tables Multiplication Arrondir des décimaux Rapporteur et Angles Médiatrice Symétrie Axiale d'un triangle Symétrie Centrale d'un triangle Translation d'un triangle Rotation Homothétie Bissectrice Tracer droite parallèle Conversion Aires et Volumes Addition de deux relatifs Soustraction Relatifs Addition et soustraction de trois relatifs Produit Deux Relatifs Produit Trois Relatifs Quotient Relatifs Carré Entier Racine Carrée Théorème Pythagore Liste Diviseurs Décomposition Facteurs Premiers Calcul du PGCD PGCD Algorithme Euclide Test Nombre Premier Déterminer Fonction Linéaire Déterminer Fonction Affine Traceur Courbe Trigonométrie Angle Trigonométrie Longueur Périmètre d'un Cercle Aire d'un Disque Volume du Parallélépipède Rectangle Volume du cylindre Surface d'une Sphère et Volume d'une boule Volume d'une pyramide à base rectangulaire Section d'une pyramide Visualiser Section Cône en 2D Section d'un Cône Carte Mondiale Coordonnées Géographiques

Mathématiques Web c'est 2 252 920 fiches de cours et d'exercices téléchargées.