Angle : cours de maths en 5ème à télécharger en PDF.

sommaire

1 I. Angle et parallélisme
- - 1.0.1 1.Les angles adjacents
  - 1.0.2 2. Angles correspondants et angles alternes-internes

Les angles à travers un cours de maths en 5ème. L’élève devra savoir tracer et mesurer un angle à l’aide du rapporteur et développer des compétences et effectuer des démonstrations en utilisant les propriétés sur les angles correspondants, opposés par le sommet et les angles alternes-internes ou alternes-externes et les droites parallèles en cinquième. Cette leçon sur les angles correspondants, opposés et alternes-internes ainsi que la position de deux droites et les propriétés des angles en cinquième vous permettra de progresser davantage en géométrie.

I. Angle et parallélisme

1.Les angles adjacents

Définition :

Deux angles sont dits adjacents si ils ont leur sommet en commun ainsi qu’un côté en commun et si ils sont situés de part et d’autre de ce côté en commun.

Exemple :

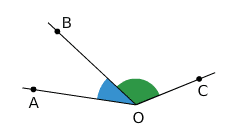
Les angles $\widehat{AOB}$ et $\widehat{BOC}$ ont comme sommet commun le point O, comme côté commun la demi-droit [OB) et ils sont placés de part et d’autre de [OB) : ils sont donc adjacents.

Remarque :

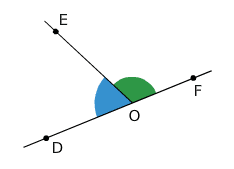
Les angles adjacents $\widehat{DOE}$ et $\widehat{EOF}$ partagent un angle plat. Leur somme est donc égale à 180 °. On dit qu’ils sont supplémentaires.

2. Angles correspondants et angles alternes-internes

Définition :

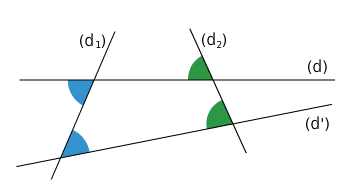
Les angles bleus sont alternes-internes.C’est-à-dire qu’ils sont déterminés par les droites (d), (d’) et la sécante (d_1) .

Les angles verts sont correspondants. C’est-à-dire qu’ils sont déterminés par les droites (d), (d’) et la sécante (d_2) .

Propriété :

Deux angles alternes-internes ont la même mesure si, et seulement si, les deux droites coupées par la sécante sont parallèles.

Deux angles correspondants ont la même mesure si, et seulement si, les deux droites coupées par la sécante sont parallèles.

Exemple :

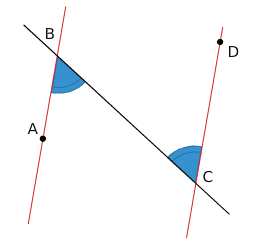
Les angles $\widehat{ABC}$ et $\widehat{BCD}$ sont alternes-internes car ils sont déterminés par la sécante (BC) et les droites (AB) et (CD).

De plus, le codage indique qu’ils ont la même mesure. Donc les droites (AB) et (CD) sont parallèles.

Exemple :

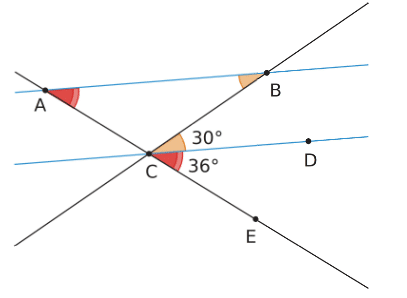
On sait que les droites (AB) et (CD) sont parallèles.

Les angles correspondants $\widehat{CAB}$ et $\widehat{ECD}$ sont déterminés par la sécante (AC) et les droites (AB) et (CD), parallèles entres elles. Ils ont donc la ,même mesure. Donc $\widehat{CAB}=\widehat{ECD}=36^{\circ}$ .
Les angles alternes-internes $\widehat{CBA}$ et $\widehat{DCB\,}$ sont déterminés par la sécante (BC) et les droites (AB) et (CD) , parallèles entre elles. Ils ont donc la même mesure. Donc $\widehat{CBA}=\widehat{DCB}=30^{\circ}$ .