Intégrales : exercices de maths en terminale corrigés en PDF.

Les intégrales et le calcul de primitive avec des exercices de maths en terminale corrigés à télécharger gratuitement au format pdf.

Ces énoncés font intervenir le calcul et la détermination d’une primitive ainsi que toutes les propriétés de l’opérateur intégral.

Ces fiche porte sur les notions suivantes :

primitives;
linéarité de l’intégrale;
somme de deux intégrales;
intégration par parties.

L’élève doit impérativement être à l’aise avec la notion de dérivée afin de pouvoir déterminer une primitive d’une fonction et, par conséquent, pouvoir calculer une intégrale. Ces énoncés sur l’intégration sont accompagnés de leur correction afin de vous permettre de relever vos erreurs et augmenter vos notes en terminale.

Exercice n° 1 :

Calculer la valeur des deux intégrales suivantes :

$a)\int_{0}^{4}3dx\,\,\,;\,\,\,b)\int_{3}^{7}\,(\,\frac{1}{2}t+2dt\,\,)$

Exercice n° 2 :

f est la fonction définie sur $\mathbb{R}$ par $f(x)=\frac{e^x}{\,(e^x+1\,\,)^2}$ .

Pour chacune des fonctions définies ci-dessous, dire s’il s’agit d’une primitive de f sur $\mathbb{R}$ .

$F_1(x)=\frac{-1}{e^x+1}\\F_2(x)=\frac{2e^x+1}{e^x+1}\\F_3(x)=\frac{2e^{-x}+1}{e^{-x}+1}\\F_4(x)=\frac{e^{-x}+2}{e^{-x}+1}$

Exercice n° 3 :

Déterminer une primitive sur $\mathbb{R}$ des fonctions numériques suivantes :

$a)\,f(x)=5x^4-3x+7\,,\,I=\mathbb{R}\\b)\,g(x)=4(3x-1)^5\,,\,I=\mathbb{R}\\c)\,\,h(x)=\frac{7x}{x^2+4}\,,\,I=]-4;+\infty[\\d)\,i(x)=3xe^x\,,\,I=\mathbb{R}$

Exercice n° 4 :

a) Démontrer que pour tout réel t de l’intervalle [0;1],

$2-2e^t\leq\,\,\,2-2e^t\leq\,\,0$

b) Démontrer que, pour tout nombre réel t de l’intervalle $[1;+\infty[$

$2-2e^{t^2}\leq\,\,2-2e^t$

c) En déduire :

un encadrement de $\int_{0}^{1}(2-2e^{t^2})dt$
l’inégalité $\int_{1}^{5}(2-2e^{t^2})dt\leq\,\,8+2(e-e^5)$

Exercice n° 5 :

Démontrer que pour tout entier naturel n,

$0\leq\,\,\int_{0}^{1}\frac{x^n}{1+x}dx\leq\,\,ln2$

Exercice n° 6 :

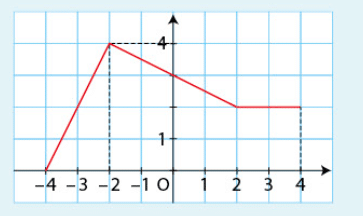
Dans le repère orthonormé ci-dessous, on a tracé la courbe représentative d’une fonction f définie

et continue sur l’intervalle [-4;4].

Calculer les intégrales suivantes :

$a)\,\int_{-4}^{-2}f(t)dt\\b)\,\int_{-2}^{2}f(t)dt\\c)\,\int_{2}^{4}f(t)dt$

Exercice n° 7 :

Calculer chacune des intégrales suivantes :

$a)\int_{-2}^{1}5dx\\b)\int_{-1}^{2}(-t+4)dt\\c)\int_{-3}^{3}(x+3)dx\\d)\int_{0}^{5}(2x+1)dx\\e)\int_{-2}^{2}\,(\,1-\frac{x}{2}\,\,)dx\\f)\,\int_{-1}^{1}\,(\,1-\,|\,x\,\,|\,\,)dx$

Exercice n° 8 :

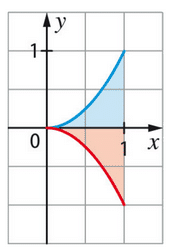
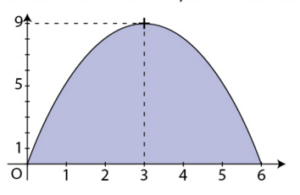
Sur le graphique ci- dessous sont tracées les courbes représentatives des
fonctions f et g définies sur [0 ; 1] par et et deux surfaces
limitées par ces courbes.

1. Calculer l’aire, en unités d’aire, de la surface colorée en bleu.

2. En déduire, sans calcul, l’aire, en unités d’aire, de la surface colorée en rouge.

3. Retrouver l’aire précédente par un calcul d’intégrale.

Exercice n° 9 :

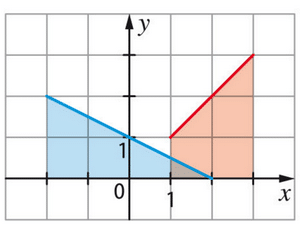
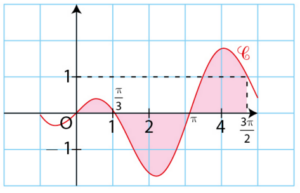
Pour l’exercice, indiquer si l’affirmation est vraie ou fausse, puis justifier.

Soit $I=\int_{1}^{3}xdx$ et $J=\int_{-2}^{2}-0,5x+1dx$ .

Par lecture graphique sur le schéma ci-contre I = J.

Exercice n° 10 :

Déterminer une primitive de chacune des fonctions f, g et h sur $\mathbb{R}$ par leurs expressions.

$1)f(x)=2xe^{x^2-3};g(x)=\frac{x}{x^2+4};h(x)=cos(x)sin^2(x)$

$2)f(x)=\frac{2x+1}{x^2+x+1};g(x)=\frac{x}{(x^2+1)^2};h(x)=x(x^2+5)^{-3}$

$3)f(x)=xe^{-x^2},g(x)=\frac{e^x}{e^x+1};h(x)=\frac{8x}{\sqrt{2x^2+1}}$

Exercice n° 11 :

Soit une fonction f définie sur [ – 3 ; 5 ].

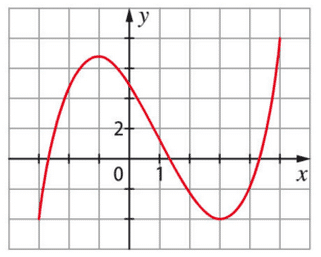
La courbe ci-dessous représente une primitive F sur [ – 3; 5 ] de f.

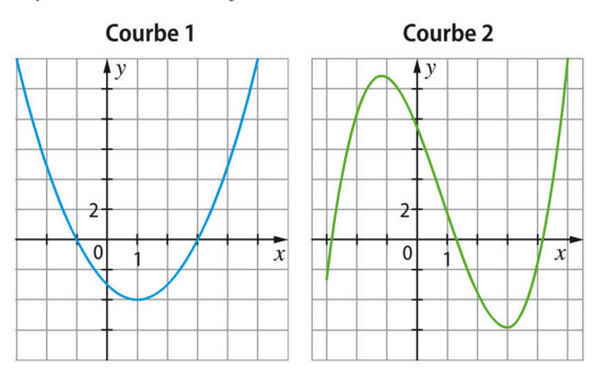
Parmi les deux courbes représentées ci-dessous, laquelle représente la fonction f? Justifier.

Exercice n° 12 :

Pour tout entier naturel n, on pose :

$I_n=\int_{n}^{n+1}\frac{1}{x}dx$

1)a) Encadrer l’inverse de x sur [ n ; n+1 ].

b) Calculer $\int_{n}^{n+1}\frac{1}{n}dx$ .

c) Démontrer que $\frac{1}{n+1}\leq\, I_n\leq\, \frac{1}{n}$

2) En déduire la limite de la suite (I_n)

Exercice n° 13 :

g est la fonction définie sur $\mathbb{R}$ par $g(x)=\,(2cos(x)\,-\,l)sin(x)$ .
Voici la courbe représentative de la fonction g dans un repère orthogonal.

Calculer l’aire, en unité d’aire, du domaine coloré sur le graphique.

Exercice n° 14 :

f est la fonction définie sur $[0;\,+\infty[$ par : $f(x)=\,xe^{-x}$ .
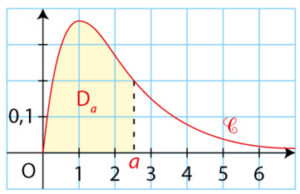
On note $\varphi$ sa courbe représentative dans un repère orthogonal.

a) Justifier que la courbe $\varphi$ est au-dessus de l’axe des abscisses.
b) Pour tout réel $a\geq\,\,0$ , on note D_a

le domaine situé sous la courbe $\varphi$ sur l’intervalle $[0;\,a]$ .
A l’aide d’une intégration par parties, exprimer l’aire, en u.a., du domaine D_a

en fonction de a.
c) Déterminer la limite de cette aire lorsque a tend vers $+\infty$ .

Exercice n° 15 :

Dans un repère orthogonal, on a tracé la courbe représentative de la fonction f définie sur [0 ; 6] par :

est l’aire du domaine coloré, en unité d’aire.

Pour tout réel

, on note

la droite d’équation y=mx

.
Déterminer, si elles existent, les valeurs de

pour lesquelles l’aire du domaine compris entre $\varphi$ et D_m

est égale à un huitième de

Voir Exercices 11 à 20...

Consulter le corrigé de cet exercice de maths

Télécharger puis imprimer cette fiche en PDF.

Télécharger ou imprimer cette fiche «intégrales : exercices de maths en terminale corrigés en PDF.» au format PDF afin de pouvoir travailler en totale autonomie.

Vous devez vous inscrire ou vous connecter à votre compte afin de pouvoir télécharger ce document au format PDF.

Réviser les cours et exercices avec nos Q.C.M :

Q.C.M en 6ème Q.C.M en 5ème Q.C.M en 4ème Q.C.M en 3ème Q.C.M en 2de Q.C.M en 1ère Q.C.M en Terminale

D'autres ressources pour progresser en autonomie :

Chronomètre Horloge France Tables Multiplication Arrondir des décimaux Rapporteur et Angles Médiatrice Symétrie Axiale d'un triangle Symétrie Centrale d'un triangle Translation d'un triangle Rotation Homothétie Bissectrice Tracer droite parallèle Conversion Aires et Volumes Addition de deux relatifs Soustraction Relatifs Addition et soustraction de trois relatifs Produit Deux Relatifs Produit Trois Relatifs Quotient Relatifs Carré Entier Racine Carrée Théorème Pythagore Liste Diviseurs Décomposition Facteurs Premiers Calcul du PGCD PGCD Algorithme Euclide Test Nombre Premier Déterminer Fonction Linéaire Déterminer Fonction Affine Traceur Courbe Trigonométrie Angle Trigonométrie Longueur Périmètre d'un Cercle Aire d'un Disque Volume du Parallélépipède Rectangle Volume du cylindre Surface d'une Sphère et Volume d'une boule Volume d'une pyramide à base rectangulaire Section d'une pyramide Visualiser Section Cône en 2D Section d'un Cône Carte Mondiale Coordonnées Géographiques

Mathématiques Web c'est 2 253 864 fiches de cours et d'exercices téléchargées.