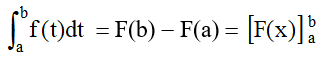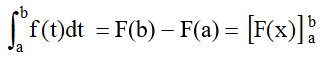Intégrales et primitives : cours de maths en terminale en PDF.

Sommaire de cette fiche

Les intégrales et les primitives avec un cours de maths en terminale à télécharger gratuitement en PDF.

Nous verrons dans cette leçon la définition et les différentes propriétés de l’intégrale ainsi que la signification géométriques avec les aires. De plus, dans ce cours, vous verrez les différentes façons de calculer une intégrale à l’aide de la primitive et des propriétés d’associativité et de linéarité de l’intégrale. En outre, les intégrales et les primitives sont à maîtriser pour bien progresser en maths.

I. Définitions et propriété de l’intégrale et des primitives.

Vocabulaire :

Une fonction f est intégrable sur un intervalle I lorsqu’elle admet des primitives sur cet intervalle I.
En particulier, les fonctions dérivables sur un intervalle I, sont intégrables sur I, mais cette condition, bien que suffisante n’est pas nécessaire. La fonction f définie sur $\mathbb{R}$ par

, bien que non dérivable en 0 est intégrable sur $\mathbb{R}$ , car elle a pour primitive sur $\mathbb{R}$ la fonction F telle que:

.
Cependant, sauf cas particulier contenant des indications, dans les problèmes de bac, les fonctions intégrables sur un intervalle I seront toujours des fonction dérivables sur I.

Propriété :

Si F et G sont deux primitives d’une fonction intégrable sur un intervalle I,
alors quels que soient a $\in$ I et b $\in$ I, on a:
F(b) – F(a) = G(b) – G(a)En effet, si F ‘(x) = G ‘(x), alors, il existe c $\in$ $\mathbb{R}$ tel que G(x) = F(x) + c.
Donc: G(b) – G(a) = F(b) + c – [F(a) + c] = F(b) – F(a).

Remarque:

La différence des images de b et de a, pour n’importe quelle primitive de f est la même.

Ce nombre ne dépend donc que de f, de a et b.

Ceci va nous permettre de donner la définition suivante:

Définition :

Soit f une fonction intégrable sur un intervalle I,
Soient a $\in$ I et b $\in$ I deux réels de cet intervalle I,
L’intégrale de a à b de la fonction f est le nombre F(b) – F(a) où F est une primitive quelconque de f sur I.

Notation:

$F(b) - F(a) = \int_{a}^{b}f(t)dt$ qui se lit « somme de a à b de f de t dt » et qui se dit aussi « intégrale de f entre a et b« .

Dans l’écriture $\int_{a}^{b}f(t)dt$ , la lettre t est appelée: « variable muette ».
En effet, on peut aussi écrire $\int_{a}^{b}f(t)dt=\int_{a}^{b}f(u)du=\int_{a}^{b}f(x)dx$ , car la lettre « variable muette » indique le nom de la « variable d’intégration » (toute autre lettre dans l’expression de la fonction f à intégrer est alors considérée comme constante. L’intérêt de ceci apparaît lorsqu’il y a plusieurs variables, mais ceci n’est pas au programme de Terminale, cependant, cela sera utile en présence de paramètres.)

$\int_{a}^{b}f(t)dt$ s’écrit aussi sous la forme condensée utilisant F :

Exemple :

La fonction $f:x \mapsto x^2$ est dérivable sur $\mathbb{R}$ .

Elle est donc intégrable sur $\mathbb{R}$ et admet des primitives sur $\mathbb{R}$ .

Par exemple $F:x \mapsto \frac{x^3}{3}$ est une primitive de f sur $\mathbb{R}$ .

On a donc:

II.Conséquences de la définition: premières propriétés.

Propriétés :

Soit f une fonction dérivable sur un intervalle [a,b]. $\int_{a}^{a}f(t)dt=0$

$\int_{a}^{b} f(t)dt=-\int_{b}^{a}f(t)dt$

Propriété :

Si f est dérivable sur I, si a $\in$ I et b $\in$ I, on a: $f(b)-f(a)=\int_{a}^{b}f'(t)dt$

On déduit de cette propriété une importante synthèse qui relie une fonction dérivable, sa fonction dérivée et la notion d’intégrale.

Théorème :

Si f est une fonction dérivable sur I et si a $\in$ I.
Alors, pour tout x $\in$ I, on a $f(x) = f(a) +\int_{a}^{x}f'(t)dt$

III.Fonction primitive d’une fonction intégrable.

Théorème :

Si f est une fonction intégrable sur un intervalle I et si a $\in$ I, alors
la fonction

définie sur I par $F_a(x) = \int_{a}^{x}f (t)dt$

est la primitive de f qui s’annule en x = a.

Démonstration :
Si G est une primitive quelconque de f sur I, alors $F_a(x) = \int_{a}^{x}f (t)dt=G(x)-G(a)$ , donc
F_a‘(x) = G ‘(x) = f(x) .

En effet, G(a) est une constante, sa dérivée est donc nulle et G ‘(x) = f(x) car G est une primitive de f. Conclusion: est aussi une primitive de f .
De plus: F_a(a) = G(a) – G(a )= 0, donc F_a s’annule pour x=a .

Exercice :

Calculer les intégrales suivantes, puis indiquer les primitives qu’elles définissent.
$F(x)=\int_{0}^{x}(2t)dt$ $G(x)=\int_{1}^{x}(3t^2)dt$ $H(x)=\int_{-1}^{x}( 3t^2+ 2t+1)dt$

IV. Intégrale d’une fonction positive.

Propriété:

On suppose ici que f est intégrable et positive sur [a;b], c’est à dire que pour tout x $\in$ [a;b], on a: f(x) $\geq\,$ 0.
Appelons F une primitive de f sur [a;b].On a alors F ‘(x) = f(x) pour tout x $\in$ [a;b].La dérivée f de F étant positive sur [a;b], la fonction F est croissante sur [a;b].Comme a < b, on a donc: F(a) $\leq\,$ F(b).
Donc: $\int_{a}^{b} f(t)dt=F(b)-F(a)\geq\, 0$

Propriété:

Si a < b et si pour tout x $\in$ [a;b] on a f(x) $\geq\,$ 0 alors $\int_{a}^{b} f(t)dt \geq\, 0$

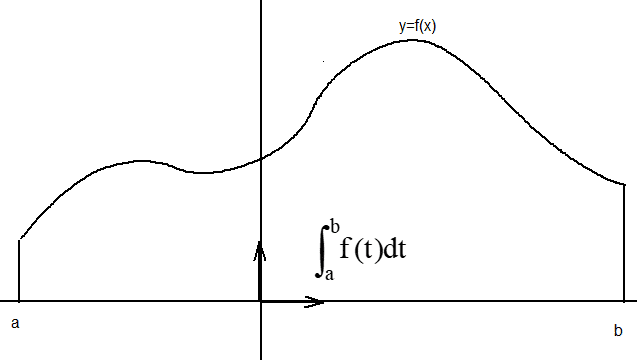
V. Les intégrales et les aires

1.Tableau récapitulatif

Propriété:

Dans un repère orthogonal $(O,\vec{i},\vec{j})$

, on représente graphiquement une fonction f dérivable et positive sur un intervalle [a;b].On appelle D l’ensemble des points du plan dont les coordonnées (x;y) vérifient :
a $\leq\,$ x $\leq\,$ b et 0 $\leq\,$ y $\leq\,$ f(x)Alors Aire de D = $\int_{a}^{b}f(t)dt$

unités d’aireL’unité d’aire étant celle du rectangle dont les côtés sont les unités de longueur des abscisses et des ordonnées.
L’ensemble D est constitué des points situés entre la courbe représentative de la fonction f, l’axe des abscisses et les droites d’équation x = a et x = b.

5/5 - (3 votes)

Télécharger puis imprimer cette fiche en PDF.

Télécharger ou imprimer cette fiche «intégrales et primitives : cours de maths en terminale en PDF.» au format PDF afin de pouvoir travailler en totale autonomie.

D'autres cours et exercices à consulter

Mathématiques Web c'est 2 268 057 fiches de cours et d'exercices téléchargées.