Corrigé des exercices sur les limites de fonctions en terminale.

EXERCICE 1 :

1. Soit $\alpha>0$ . On cherche à montrer que l’intervalle $]1-\alpha;1+\alpha[$ contient toutes les valeurs de g(x) pour x assez grand.

Pour tout x>0, on a :
$g(x)=\frac{1}{x}+1=\frac{x+1}{x}=\frac{x}{x}+\frac{1}{x}=1+\frac{1}{x}$ .

Ainsi, si $x>\alpha$ , on a :
$1-\alpha<\frac{1}{x}<1+\alpha$ ,
ce qui entraîne :
$1-\alpha+1<1+\frac{1}{x}<1+\alpha+1$ ,
soit :
$2-\alpha<g(x)<2+\alpha$ .

Donc, pour tout $x>\alpha$ , on a $g(x)\in]2-\alpha;2+\alpha[$ et l’intervalle $]1-\alpha;1+\alpha[$ contient toutes les valeurs de g(x) pour x assez grand.

2. On en déduit que :
$\lim_{x\to+\infty}g(x)=2$ .
Graphiquement, cela signifie que la courbe de g se rapproche de la droite d’équation y=2 lorsque x tend vers l’infini.

EXERCICE 2 :

1. Soit $\alpha>0$ . On cherche à montrer que l’intervalle $]-\alpha;+\alpha[$ contient toutes les valeurs de h(x) pour x assez grand.

Pour tout x>1, on a :
$h(x)=\frac{1}{x^2-1}=\frac{\frac{1 }{x^2}}{1-\frac{1 }{x^2}}$ .

Comme $1-\frac{1}{x^2}$ tend vers 1 lorsque x tend vers l’infini, on peut choisir x assez grand pour que $1-\frac{1}{x^2}>\frac{1}{2}$ , ce qui donne :
$\frac{1}{2}<1-\frac{1}{x^2}<1$ .

D’autre part, comme $\frac{1}{x^2}$ tend vers 0 lorsque x tend vers l’infini, on peut choisir x assez grand pour que $\frac{1}{x^2}<\alpha^2$ , ce qui donne :
$0<\frac{1}{x^2}<\alpha^2$ .

On en déduit que, pour x assez grand :
$-\alpha<\frac{1}{x^2-1}<\alpha$ ,
ce qui montre que l’intervalle $]-\alpha;+\alpha[$ contient toutes les valeurs de h(x) pour x assez grand.

2. On en déduit que :
$\lim_{x\to+\infty}h(x)=0$ .
Graphiquement, cela signifie que la courbe de h se rapproche de l’axe des abscisses lorsque x tend vers l’infini.

EXERCICE 3 :

On a :
.

Le trinôme du second degré admet deux racines réelles et distinctes :

$x_1=\frac{3-\sqrt{13}}{2}$ et $x_2=\frac{3+\sqrt{13}}{2}$ .

Ainsi, lorsque x tend vers l’infini, le terme -x^2 domine et f(x) tend vers $-\infty$ .

EXERCICE 4 :

a) Pour tout $x\in\mathbb{R}$ , on a :
$g(x)=\frac{e^x+1}{e^x-1}=\frac{e^x}{e^x-1}+\frac{1}{e^x-1}=1+\frac{1}{e^x-1}$ .

En posant y=e^{-x}, on a :
$\lim_{x\to-\infty}g(x)=\lim_{y\to+\infty}g(-\ln y)=1+\lim_{y\to+\infty}\frac{1}{y-1}=1$ .

Ainsi, la fonction g admet une limite finie en $-\infty$ , égale à 1.

b) Pour tout $x\in\mathbb{R}$ , on a :
$g(x)=\frac{e^x+1}{e^x-1}=\frac{1+\frac{1}{e^x}}{1-\frac{1}{e^x}}=1+\frac{2}{e^x-1}$ .

En posant , on a :
$\lim_{x\to+\infty}g(x)=\lim_{y\to+\infty}g(\ln y)=1+\lim_{y\to+\infty}\frac{2}{y-1}=1$ .

Ainsi, la fonction g admet une limite finie en $+\infty$ , égale à 1.

EXERCICE 5 :

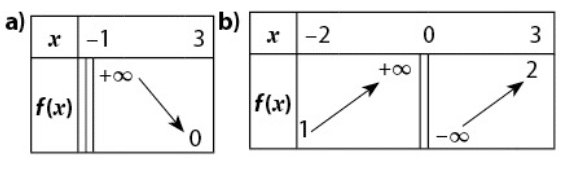
Il est difficile de donner une réponse graphique sans les axes gradués, mais voici quelques idées pour tracer une courbe $\varphi$ qui respecte le tableau de variation donné :

– Pour la fonction croissante puis décroissante, on peut tracer une courbe en forme de montagne, avec un sommet qui correspond au maximum, puis une descente jusqu’à l’asymptote horizontale (qui correspond au pointillé horizontal en bas à droite du tableau).
– Pour la fonction décroissante puis croissante, on peut tracer une courbe en forme de vallée, avec un point minimum qui correspond à l’intersection du pointillé horizontal et du pointillé vertical à gauche du tableau, puis une montée jusqu’à l’asymptote horizontale.
– Pour la fonction constante puis décroissante, on peut tracer une droite horizontale jusqu’au pointillé vertical à gauche du tableau, puis une descente brusque jusqu’à l’asymptote horizontale.
– Pour la fonction décroissante puis constante, on peut tracer une descente brusque jusqu’au pointillé vertical à gauche du tableau, puis une droite horizontale jusqu’à l’asymptote horizontale.

EXERCICE 6 :

$\\\\a) \lim_{x\to+\infty}f(x)=\lim_{x\to+\infty}x\sqrt{x}=\lim_{x\to+\infty}x^\frac{3}{2}=+\infty. \\\\b) \lim_{x\to+\infty}g(x)=\lim_{x\to+\infty}\frac{(4x^2-x+5)(x-1)}{(x+1)(x-1)}=\lim_{x\to+\infty}(4x-5)=+\infty. \\\\c)\lim_{x\to+\infty}h(x)=\lim_{x\to+\infty}e^x\,(\frac{1}{x}+2)=+\infty\times 2=+\infty. \\\\d)\lim_{x\to+\infty}k(x)=\lim_{x\to+\infty}x^2\,(-3-\frac{1}{x}\,)=\lim_{x\to+\infty}-3x^2=-\infty.$

EXERCICE 7 :

1.
a. On peut utiliser la fonction graphique de la calculatrice pour représenter la courbe de C.

On voit que la fonction est croissante et tend vers l’asymptote horizontale y=8 pour x qui tend vers l’infini.

b. On a :

$\lim_{x\to+\infty}C(x)=\lim_{x\to+\infty}\frac{8}{1+e^{-x}}=8$ .

2.
a. Le coût moyen de fabrication d’une puce lorsqu’on en fabrique q est donné par :
$C_M(q)=\frac{C(q)}{q}=\frac{8}{q(1+e^{-q})}$ .

b. On peut tracer la courbe de à l’aide de la fonction graphique de la calculatrice. On voit que la fonction est décroissante et tend vers zéro pour q qui tend vers l’infini.

c. On a :
$\lim_{q\to+\infty}C_M(q)=\lim_{q\to+\infty}\frac{8}{q(1+e^{-q})}=0$ .

Interprétation :

lorsque la quantité de puces fabriquées augmente, le coût moyen de fabrication diminue et tend vers zéro.

Cela peut s’expliquer par des phénomènes d’économies d’échelle : plus la production est importante, plus les coûts fixes sont dilués sur une grande quantité de puces, ce qui permet de réduire le coût moyen de fabrication.