Corrigé des exercices sur les suites numériques en terminale.

EXERCICE N°1 :

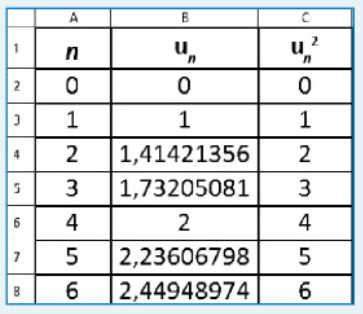
En observant les premières valeurs de et , on peut conjecturer que $u_n=\sqrt{4^n-1}$ pour tout $n\in\mathbb{N}$ .

On peut le démontrer par récurrence.
Initialisation :

Pour n=0, on a $u_0=0=\sqrt{4^0-1}$ . L’hypothèse est vérifiée au rang 0.
Hérédité :

Supposons que $u_n=\sqrt{4^n-1}$ vraie pour un certain entier n.

Alors,
$u_{n+1}=\sqrt{u_n^2+1}=\sqrt{(4^n-1)+1}=\sqrt{4^{n+1}-1}$ .
Ainsi, l’hypothèse est vérifiée au rang .
Conclusion :

On en déduit que $u_n=\sqrt{4^n-1}$ pour tout $n\in\mathbb{N}$ .

EXERCICE N°2 :

Initialisation :

Pour n=0, on a . L’hypothèse est vérifiée au rang 0.

Hérédité :

Supposons que soit vraie pour un certain entier n.

Alors,
$V_{n+1}=V_n+2n+2=(n+1)(n+2)= (n+1)((n+1)+1)$ .
Ainsi, l’hypothèse est vérifiée au rang .

Conclusion :

On en déduit que pour tout $n\in\mathbb{N}, V_n=n(n+1)$ .

EXERCICE N°3 :

Initialisation :

Pour n=0, on a $2^0=1\geq\, 1+1$ .

L’hypothèse est vérifiée au rang 0.
Hérédité :

Supposons $2^n\geq\, n+1$ pour un certain entier n.

On a alors :
$2^{n+1}=2\times 2^n\geq\, 2(n+1)\geq\, n+2+1$ .
Ainsi, l’hypothèse est vérifiée au rang .
Conclusion :

On en déduit que $2^n\geq\, n+1$ pour tout entier naturel n.

EXERCICE N°4 :

Initialisation :

Pour n=0, on a $OA_0=1=\sqrt{4\times 0+1}$ .

L’hypothèse est vérifiée au rang 0.
Hérédité :

Supposons que $OA_n=\sqrt{4n+1}$ pour un certain entier n.

On a alors :
$OA_{n+1}=\sqrt{OA_n^2+A_nA_{n+1}^2}=\sqrt{(4n+1)+4}=\sqrt{4(n+1)+1}$ .
Ainsi, l’hypothèse est vérifiée au rang .
Conclusion :

On en déduit que $OA_n=\sqrt{4n+1}$ pour tout $n\in\mathbb{N}$ .

EXERCICE N°5 :

1) a) On a $\lim_{n\to \infty}0,9^n=0$ et donc $\lim _{n\to \infty}u_n=3(2-0)=6$ .
b) On a $\lim _{n\to \infty}1,01^n=+\infty$ et donc $\lim _{n\to \infty}v_n=+\infty$ .
c) On a $\lim _{n\to \infty}0,9^n=0$ et $\lim _{n\to \infty}3+0,2^n=3$ , donc $\lim _{n\to \infty}w_n=\frac{3}{0-5}=-\frac{3}{5}$ .
d) On peut réécrire sous la forme \frac{4^n}{3^n}+\frac{5}{3^n}. On a $\lim _{n\to \infty}\frac{4^n}{3^n}=+\infty$ et $\lim _{n\to \infty}\frac{5}{3^n}=0$ , donc $\lim _{n\to \infty}t_n=+\infty$ .

2) a) Le premier terme de la suite est -3.

On peut écrire $S_n=\frac{-3(1-0,8^n)}{1-0,8}$ .

En effet,

$S_n=u_1(1+0,8+0,8^2+...+0,8^{n-1})=-3(1+0,8+0,8^2+...+0,8^{n-1})=-3\frac{1-0,8^n}{1-0,8}$ .
b) La suite est convergente car , et sa limite est $\frac{-3}{1-0,8}=15$ .

EXERCICE N°6 :

On a $u_n=(-3)\times 0,8^{n-1}$ .

Ainsi, $S_n=-3\frac{1-0,8^n}{1-0,8}=3(0,8^n-1)$ .

On en déduit que la limite de la suite est $3\times (-1)=-3$ .

EXERCICE N°7 :

1) a) La fonction f est dérivable sur $]0;+\infty[$ et on a $f'(x)=\frac{3}{(1+2x)^2}>0$ pour tout .

Donc, f est strictement croissante sur $[0;+\infty[$ .
b) Si $x\in[0;1]$ , alors $f'(x)=\frac{3}{(1+2x)^2}\leq\, \frac{3}{(1+2\times 1)^2}=1$ .

2) Initialisation :

Pour n=0, on a $u_0=0,7\geq\, 0 et u_0\leq\, 1$ .

L’hypothèse est vérifiée au rang 0.

Hérédité :

Supposons que $0\leq\, u_n\leq\, 1$ pour un certain entier n soit vraie.

Alors, $0\leq\, 3u_n\leq\, 3$ et $0\leq\, 2u_n<2$ , donc
$0\leq\, u_{n+1}=\frac{3u_n}{1+2u_n}<\frac{3}{1}=3$

et
$0\leq\, u_{n+1}=\frac{3u_n}{1+2u_n}\geq\, 0$ .
Ainsi, l’hypothèse est vérifiée au rang.

Conclusion :

On en déduit que pour tout $n\in\mathbb{N}, 0\leq\, u_n\leq\, 1$ .

3) La suite est décroissante et minorée par 0, donc elle converge.

Soit l sa limite.

En passant à la limite dans la relation de récurrence, on a $l=\frac{3l}{1+2l}$ .

Cette équation admet comme solution, qui est la seule solution possible car f est strictement croissante sur [0;1].

Ainsi, la suite converge vers 0.

EXERCICE N°8 :

1) Les dix premiers termes de la suite sont :
1, 4, 9, 16, 25, 36, 49, 64, 81, 100.

2) a) On peut conjecturer que u_n=n^2.

b) Initialisation :

Pour n=1, on a . L’hypothèse est vérifiée au rang 1.
Hérédité :

Supposons que pour un certain entier n.

Alors,
$u_{n+1}=u_n+2n+1=n^2+2n+1=(n+1)^2$ .
Ainsi, l’hypothèse est vérifiée au rang n+1.
Conclusion :

On en déduit que pour tout $n\in\mathbb{N}, u_n=n^2$ .

EXERCICE N°9 :

Initialisation :

Pour n=1, on a $1^2=\frac{1\times 2\times 3}{6}$ .

L’hypothèse est vérifiée au rang 1.
Hérédité :

Supposons $\sum\limits_{q=1}^{n}q^2=\frac{n(n+1)(2n+1)}{6}$ .

Alors,
$\sum\limits_{q=1}^{n+1}q^2 \\\\=\sum\limits_{q=1}^{n}q^2+(n+1)^2=\frac{n(n+1)(2n+1)}{6}+(n+1)^2 \\\\(n+1)\,\frac{2n^2+7n+6}{6} \\\\(n+1)\,\frac{(n+1)(2n+3)}{6} \\\\=\frac{(n+1)(n+2)(2n+3)}{6}$ .

Ainsi, l’hypothèse est vérifiée au rang n+1.
Conclusion :

On en déduit que pour tout entier naturel n non nul,

$\sum_{q=1}^{n}q^2=\frac{n(n+1)(2n+1)}{6}$ .

EXERCICE N°10 :

1) a) On a $\lim\limits_{n\to \infty}u_n=\lim\limits_{n\to \infty}\frac{4^n+5}{2\times 3^n}=0$ car $\frac{4^n+5}{2\times 3^n}\leq\, \frac{4^n+5^n}{2\times 3^n}= (\frac{4}{5})^n+\frac{5}{2}\times (\frac{2}{3})^n$ qui tend vers 0 quand n tend vers l’infini.

b) On a $\lim\limits_{n\to \infty}v_n=\lim\limits_{n\to \infty}(1+\frac{2n-5}{3+2n})=1$ .
c) On a $l=\lim\limits_{n\to \infty}\frac{4n-1+\frac{5}{\sqrt{n}}}{n}=4+\lim\limits_{n\to \infty}\frac{5}{n^{\frac{3}{2}}}=4$ .

d) On a $\lim\limits_{n\to \infty}t_n=+\infty$ .

2) a) La suite est géométrique de raison 0,8 et de premier terme -3.

Ainsi, $u_n=(-3)\times 0,8^{n-1}$ .

b) On a $\lim\limits_{n\to \infty}u_n=\lim\limits_{n\to \infty}(-3)\times 0,8^{n-1}=0$ .

3) Les trois dernières suites tendent toutes vers 0, donc elles sont bornées.

EXERCICE N°11 :

1) On a $v_n=4u_n-3=4(-\frac{1}{3}u_{n-1}+1)-3=-\frac{4}{3}v_{n-1}$ .
Ainsi, la suite (v_n) est géométrique de raison $-\frac{1}{3}$ , et son premier terme est .

2) On peut écrire $v_n=4u_n-3=4(-\frac{1}{3})^n+4-3=-\frac{17}{4}\times (\frac{-1}{3})^n+\frac{1}{4}$ .
Ainsi, $u_n=\frac{17}{4}\times (\frac{-1}{3})^n+\frac{3}{4}$ .

3) La suite (u_n) tend vers $\frac{3}{4}$ .

EXERCICE N°12 :

1) On a $u_n=(\frac{1}{3})^n-8$ .

Comme $\frac{1}{3}<1$ , on a $(\frac{1}{3})^n\to 0$ lorsque $n\to+\infty$ .

Donc $u_n\to -8$ lorsque $n\to+\infty$ .

Par conséquent, la suite (u_n) est bornée.

2) On a $-1\leq\, \sin(5n+1)\leq\, 1$ pour tout entier naturel $n$.

Donc $-8\leq\, 5\sin(5n+1)-3\leq\, 2$ .

Ainsi, (u_n) est bornée.

3) La fonction $x\mapsto \cos(x)-x$ est continue et décroissante sur $\mathbb{R}$ .

On a $\cos(n^2)\in [-1,1]$ pour tout entier naturel , donc $u_n\in [-n-1,n+1]$ pour tout entier naturel $n$.

Ainsi, (u_n) est bornée.

Voir Corrigés 11 à 12...

Télécharger puis imprimer cette fiche en PDF.

Télécharger ou imprimer cette fiche «corrigé des exercices sur les suites numériques en terminale.» au format PDF afin de pouvoir travailler en totale autonomie.