Corrigé des exercices sur le logarithme en terminale.

EXERCICE N° 1 :

a) La seule solution est x=0 car .
b) On a qui donne .
c) On résout l’équation , donc qui donne x=ln2.
d) On résout l’équation $4e^{-x}=15$ , donc $e^{-x}=\frac{15}{4}$ qui donne $x=ln(\frac{4}{15})$ .
e) On résout l’équation $e^{2x-1}-2=0$ , donc $e^{2x-1}=2$ qui donne et finalement .
f) L’équation n’a pas de solution car $e^{-x}$ est toujours positif.

EXERCICE N° 2 :

a) On a .
b) On a $x=\frac{1}{2}$ .
c) On résout l’équation , donc , ce qui donne x=e^{7/2}.
d) On résout l’équation , donc , ce qui donne $x=\frac{e^3+1}{2}$ .
e) On a x=1/e.
f) On résout l’équation , donc , ce qui donne ou (mais cette dernière solution est exclue car elle n’appartient pas à l’ensemble de définition de ln).

EXERCICE N° 3 :

a) On peut simplifier $ln3+ln( \frac{1}{3})=ln( \frac{3}{3})=0$ .
b) On peut simplifier .
c) On peut simplifier $\frac{1}{2}ln \sqrt{2}=ln(\frac{ \sqrt{2}}{2})=ln(\frac{1 }{\sqrt{2}})=-ln \sqrt{2}=-\frac{1}{2}ln2$ .

EXERCICE N° 4 :

a) L’ensemble de définition est ]-∞; -1[ ∪ ]1; +∞[. On peut simplifier , donc l’équation est équivalente à , donc $1-x^2=e^{2(ln2-ln5)}=\frac{4}{25}$ , ce qui donne $x=\pm\sqrt{ \frac{21}{25} }$ .

Cependant, x=√(21/25) ne convient pas car il n’appartient pas à l’ensemble de définition, donc la seule solution est x=-√(21/25)=-√21/5.
b) L’ensemble de définition est ]3/2; +∞[.

On peut simplifier ,

donc x(x-3)=4 et finalement x=4 ou x=-1.

Cependant, x=-1 ne convient pas car il n’appartient pas à l’ensemble de définition, donc la seule solution est x=4.
c) L’ensemble de définition est ]0; 3[.

On peut simplifier , donc $-x^2+3x=\frac{4}{1}$ et finalement $x=\frac{1}{2}$ ou x=2.

Cependant, x=2 ne convient pas car il n’appartient pas à l’ensemble de définition, donc la seule solution est x=1/2.

EXERCICE N° 5 :

1. On a

, donc f(x) tends vers -∞ quand x tends vers 0 car $ln(\frac{x+1}{x})$ tends vers -∞.

On peut interpréter graphiquement ce résultat en disant que admet une asymptote verticale en x=0.
2. a) On a f(x) tends vers +∞ quand x tends vers +∞ car 2x-1 tends vers +∞ et ln(x/(x+1)) tends vers 0.
b) On a

$\lim_{x\to +\infty}[(2x-1-(y-1))/ln(1+x/(x+1))]=\lim_{x\to +\infty}(2x/(x+1))/(1+x/(x+1))=2$

, donc y=2x-1 est une asymptote oblique à en +∞.

On peut dire que est située en dessous de la droite y=2x-1 car pour tout x.
3. On résout l’inéquation $1-e^{ 2x } \geq\, 0$ , donc $e^{2x} \leq\, 1$ , ce qui donne x≤0. On peut également écrire l’inéquation sous la forme $e^{2x} \geq\, 1$ , c’est à dire x≥0, mais cette solution n’appartient pas à l’ensemble de définition de ln.
4. On cherche à résoudre l’équation $2x-1+ln(\frac{x}{x+1})=0$ .

On peut réécrire l’équation sous la forme $ln(\frac{x}{x+1})=-2x+1$ , donc $\frac{x}{x+1}=e^{-2x+1}$ , ce qui donne l’équation $x+xe^{-2x+1}=1$ .

On sait que l’équation a une unique solution dans $]0;+\infty[$ car $x+xe^{-2x+1}$ est une fonction croissante dans cet intervalle (puisque sa dérivée est $1-2xe^{-2x+1}>0$ ).

En utilisant la méthode de dichotomie, on trouve que la solution est .
5. Voir figure ci-dessous.

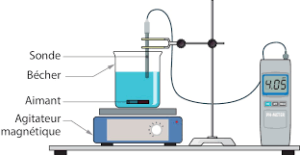
EXERCICE N° 6 :

1. On a $pH=-log[H_3O^+]=-log(5 \times 10^{-9}) \approx 8.30$ , donc la solution est basique.

Si la concentration en ions est égale à 0,1 mol/L, alors pH=-log(0,1)≈1 (la solution est acide).
2. Une solution neutre a un pH égal à 7.

On a , donc $[H_3O^+]=10^{-pH}=10^{-7}$ mol/L.
3. Si l’on augmente la concentration en ions H_3O^+, on diminue le pH de la solution car , donc une concentration plus élevée implique un logarithme plus petit (et donc un pH plus petit).
4. Pour incrémenter le pH d’une solution, il faut ajouter une base (qui réagit avec les ions pour les neutraliser) ou enlever un acide (qui libère des ions dans la solution). Pour décrémenter le pH d’une solution, il faut faire l’opposé (ajouter un acide ou enlever une base).

VOCABULAIRE : Décrémenter, c’est soustraire 1.

EXERCICE N° 7 :

1. a) On a $\lim_{x\to -\infty}ln(1+e^{2x})=-\infty$ car $e^{2x}$ tends vers 0 et ln tends vers $-\infty$ quand son argument tend vers 0.
b) En utilisant la règle de l’Hôpital, on trouve que $\lim_{x\to +\infty}[(x+2)/e^{2x}]=0$ .

Donc l’équation de l’asymptote oblique est pour une certaine constante c.

En utilisant l’expression $f(x)=2-x-ln(1+e^{-2x})$ qui est équivalente à , on trouve que c=1.

Donc l’asymptote oblique est .

c) En utilisant l’expression $f(x)=2-x-ln(1+e^{-2x})$ , on trouve que $f(-x)=2+x-ln(1+e^{2x})=f(x)+2x$ , donc l’axe des ordonnées est un axe de symétrie pour C.

d) On a $\lim_{x\to +\infty}f(x)=\lim_{x\to +\infty}(x+2-ln(e^{2x}(1+e^{2x})^{-1}))=+\infty$

car x+2 tends vers +∞ et $ln(e^{2x}(1+e^{2x})^{-1})$ tends vers -∞.

Donc il y a une seconde asymptote oblique en +∞.

En utilisant $f(x)=2-x-ln(1+e^{-2x})$ , on trouve que l’équation de cette asymptote est y=-2x.
2. On a $f(-x)=x+2-ln(1+e^{2x})=f(x)$ , donc C est symétrique par rapport à l’axe des ordonnées.
3. On résout l’équation $1-e^{2x} \geq\, 0$ comme dans l’exercice précédent et on trouve $x \leq\, 0$ .
4. On calcule la dérivée de f : $f'(x)=2-e^{2x}/(1+e^{2x})=2(1-1/(1+e^{2x}))=2(1-t/(1+t))$ où $t=e^{2x}>0$ .

La fonction est décroissante car sa dérivée est $\frac{t}{(1+t)^2}>0$ pour t>0.

Donc pour tout x, ce qui implique que f est décroissante sur $\mathbb{R}$ .

De plus, f(-x)=f(x), donc C est symétrique par rapport à l’axe des ordonnées et il suffit d’étudier les variations de f sur $[0; +\infty[$ .

On a et $\lim_{x\to +\infty}f(x)=-\infty$ , donc C intersecte l’axe des abscisses en un unique point $\alpha$ .

Pour déterminer son encadrement d’amplitude $10^{-2}$ , on utilise la méthode de dichotomie.

On trouve que $\alpha$ est plus grand que 0,69 et plus petit que 0,70.
5. Voir figure ci-dessous.

Télécharger puis imprimer cette fiche en PDF.

Télécharger ou imprimer cette fiche «corrigé des exercices sur le logarithme en terminale.» au format PDF afin de pouvoir travailler en totale autonomie.

Réviser les cours et exercices avec nos Q.C.M :

Q.C.M en 6ème Q.C.M en 5ème Q.C.M en 4ème Q.C.M en 3ème Q.C.M en 2de Q.C.M en 1ère Q.C.M en Terminale

D'autres ressources pour progresser en autonomie :

Chronomètre Horloge France Tables Multiplication Arrondir des décimaux Rapporteur et Angles Médiatrice Symétrie Axiale d'un triangle Symétrie Centrale d'un triangle Translation d'un triangle Rotation Homothétie Bissectrice Tracer droite parallèle Conversion Aires et Volumes Addition de deux relatifs Soustraction Relatifs Addition et soustraction de trois relatifs Produit Deux Relatifs Produit Trois Relatifs Quotient Relatifs Carré Entier Racine Carrée Théorème Pythagore Liste Diviseurs Décomposition Facteurs Premiers Calcul du PGCD PGCD Algorithme Euclide Test Nombre Premier Déterminer Fonction Linéaire Déterminer Fonction Affine Traceur Courbe Trigonométrie Angle Trigonométrie Longueur Périmètre d'un Cercle Aire d'un Disque Volume du Parallélépipède Rectangle Volume du cylindre Surface d'une Sphère et Volume d'une boule Volume d'une pyramide à base rectangulaire Section d'une pyramide Visualiser Section Cône en 2D Section d'un Cône Carte Mondiale Coordonnées Géographiques

Mathématiques Web c'est 2 252 922 fiches de cours et d'exercices téléchargées.