Les équations et inéquations du second degré à travers un cours de maths en 1ère au format PDF.
Cette leçon fait intervenir les notions suivantes :
– définition d’une équation et d’une inéquation du second degré à une inconnue ;
– mise sous forme canonique;
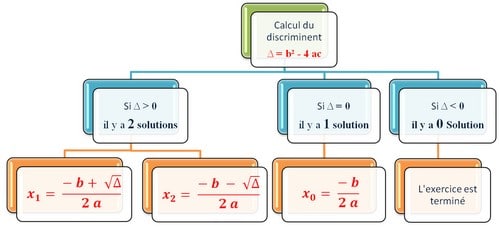
– calcul du discriminant delta;
– factorisation et signe du trinôme;
– résolution graphique.
I. Les équations en maths du second degré et les trinômes
P(x) = ax² + bx + c est un trinôme du second degré (a non nul).
II. Résolution des équations du second degré
Télécharger puis imprimer cette fiche en PDF.
Télécharger ou imprimer cette fiche «les équations et inéquations du second degré : cours de maths en 1ère en PDF.» au format PDF afin de pouvoir travailler en totale autonomie.
D'autres cours et exercices à consulter
- Trigonométrie et relations métriques : cours de maths en 1ère en PDF.
- Probabilités : cours de maths en 1ère en PDF.
- Fonction exponentielle : cours de maths en 1ère en PDF.
- Dérivée d’une fonction : cours de maths en 1ère en PDF.
- Produit scalaire : cours de maths en 1ère en PDF.
- Les fonctions et leurs variations : cours de maths en 1ère en PDF.
- Suites numériques : cours de maths en 1ère en PDF.
- Géométrie dans l’espace : cours de maths en 1ère en PDF.