Corrigé des exercices sur le produit scalaire en 1ère.

EXERCICE 1:

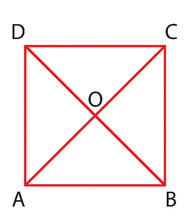
a) Comme O est le centre du carré, on a $\vec{AB}=-\vec{CD}$ et $\vec{AO}=-\vec{OD}$ (les vecteurs ont la même norme mais des directions opposées car ils sont symétriques par rapport à O).
Ainsi, $\vec{AB}.\vec{AO}=-\vec{CD}.\vec{OD}=-CD^2=-8^2=-64$ .

b) Comme O est le centre du carré, $\vec{OB}=-\vec{OA}$ et $\vec{OD}=-\vec{OC}$ (les vecteurs ont la même norme mais des directions opposées car ils sont symétriques par rapport à O).
Ainsi, $\vec{OB}.\vec{OD}=-\vec{OA}.\vec{OC}=-OA^2=-4^2=-16$ .

c) Les vecteurs $\vec{AB}$ et $\vec{AD}$ sont adjacents et forment un angle droit car ils sont des côtés du carré. Ainsi, leur produit scalaire est nul : $\vec{AB}.\vec{AD}=0$ .

d) Les vecteurs $\vec{BO}$ et $\vec{BC}$ sont adjacents et forment un angle droit car ils sont des côtés du carré. Ainsi, leur produit scalaire est nul : $\vec{BO}.\vec{BC}=0$ .

EXERCICE 2:

On utilise la formule du produit scalaire en coordonnées :

$\vec{u}.\vec{v}=u_1v_1+u_2v_2+u_3v_3$

Comme l’angle entre $\vec{u}$ et $\vec{v}$ vaut 60 degrés, on a $cos(60^{\circ})=\frac{\vec{u}.\vec{v}}{\|\vec{u}\|\|\vec{v}\|}$ ce qui donne :

$\vec{u}.\vec{v}=\|\vec{u}\|\|\vec{v}\|\cos(60^{\circ})=2\times 3\times \frac{1}{2}=3$ .

EXERCICE 3:

On utilise la formule du produit scalaire en coordonnées :

$\vec{u}.\vec{v}=u_1v_1+u_2v_2+u_3v_3$

Et on sait que $\|\vec{u}\|=6 et \|\vec{v}\|=2$ donc $\vec{u}.\vec{u}=6^2=36$ et $\vec{v}.\vec{v}=2^2=4$ .
On a également $\vec{u}.\vec{v}=-6$ .

En combinant ces informations, on obtient :

$\cos(\theta)=\frac{\vec{u}.\vec{v}}{\|\vec{u}\|\|\vec{v}\|}=\frac{-6}{6\times 2}=-\frac{1}{2}$

L’angle cherché est donc $\theta=\arccos(-\frac{1}{2})=120^{\circ}$ .

EXERCICE 4:

a) $\vec{u}.\vec{v}=u_1v_1+u_2v_2=(-2)\times (-1)+3\times (-5)=13$

b) $(4\vec{u}).\vec{v}=4(u_1v_1+u_2v_2)=4\times 13=52$

c) $(\vec{u}-\vec{v}).(\vec{u}+\vec{v})=\vec{u}.\vec{u}-\vec{v}.\vec{v}=||\vec{u}||^2-||\vec{v}||^2=4^2-(-5)^2=-9$

EXERCICE 5:

Le vecteur $\vec{AB}$ est donné par $\vec{AB}=\begin{pmatrix}1-(-3)\\3-(-2)\end{pmatrix}=\begin{pmatrix}4\\5\end{pmatrix}$ .

Le produit scalaire entre $\vec{AB}$ et $\vec{u}$ est donné par :

$\vec{AB}.\vec{u}=4\times (-5)+5\times 4=-20+20=0$ .

Comme le produit scalaire est nul, cela signifie que les vecteurs $\vec{AB}$ et $\vec{u}$ sont orthogonaux.

EXERCICE 6:

a) On utilise la propriété distributive du produit scalaire : $\vec{AB}.\vec{CD} = ( \vec{AB} + \vec{BA} ).( \vec{DC} + \vec{CD} ) = \vec{BA}.\vec{DC} + \vec{AB}.\vec{CD}$ , d’où $\vec{AB}.\vec{CD} = \vec{BA}.\vec{DC}$ .

b) On utilise la relation de Chasles : $\vec{ED} = \vec{EA} + \vec{AB} + \vec{BC} + \vec{CD}$ , d’où $\vec{AB}.\vec{ED} = \vec{AB}.\vec{EA} + \vec{AB}.\vec{AB} + \vec{AB}.\vec{BC} + \vec{AB}.\vec{CD}$ .

Or $\vec{AB}.\vec{EA} = \vec{AB}.\vec{EC}$

car $\vec{EA} = \vec{ED}+\vec{DC}+\vec{CE}, \vec{AB}.\vec{AB} = \|\vec{AB}\|^2$ ,

$\vec{AB}.\vec{BC} = \vec{AC}.\vec{BC} - \vec{AC}.\vec{AB} = 0$ car $\vec{AC}$ et $\vec{AB}$ sont orthogonaux et $\vec{AC}.\vec{BC} = 0$ car ils sont adjacents et forment un angle droit.

Ainsi, on a

$\vec{AB}.\vec{ED} = \vec{AB}.\vec{EC} + \|\vec{AB}\|^2 + \vec{AB}.\vec{CD} = \vec{AB}.\vec{AC} + \vec{AB}.\vec{EC} + \vec{AB}.\vec{CD} + \|\vec{AB}\|^2 = \vec{AB}.\vec{AC} + \vec{AB}.\vec{EC}$ ,

d’où $\vec{AB}.\vec{AC} + \vec{AB}.\vec{EC} = \vec{AB}.\vec{ED}$ .

c) On utilise la relation de Chasles : $\vec{AC} = \vec{AB} + \vec{BC}$ , d’où $\vec{AB}.\vec{AC} = \vec{AB}.\vec{AB} + \vec{AB}.\vec{BC} = \|\vec{AB}\|^2$ . On sait également que $\vec{AB}.\vec{BA} = -\|\vec{AB}\|^2$ car les vecteurs sont opposés.

En combinant ces éléments, on obtient $\vec{AB}.\vec{AC} = \vec{AB}^2 - \vec{BA}.\vec{BC}$ .

EXERCICE 7:

On utilise la relation de Chasles : $\vec{MD} = \vec{MC} + \vec{CD}$ , d’où $\vec{MC}.\vec{MD} = \vec{MC}$ .

$(\vec{MC}+\vec{CD}) \\\\= \|\vec{MC}\|^2+\vec{MC}.\vec{CD} \\\\= \|\vec{MC}\|^2 - (10-\|\vec{MC}\|)^2\\\\ = 2\|\vec{MC}\|^2-20\|\vec{MC}\|+80$ .

Cette expression est de la forme .

Le coefficient a est strictement positif, donc la fonction est une parabole ouverte vers le haut. Son minimum est atteint en $x= -\frac{b}{2a}= \frac{10}{4} = 2,5$ .

Ainsi, l’ensemble des points M vérifiant $\vec{MC}.\vec{MD}=-9$ est donc le cercle de centre H et de rayon 2,5.

EXERCICE 8:

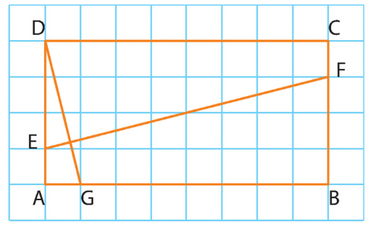
1. Dans le repère (A ; G,E), les coordonnées des vecteurs sont $\vec{AE} =\begin{pmatrix}2\\0\end{pmatrix}, \vec{AG} =\begin{pmatrix}1\\0\end{pmatrix}, \vec{CE} =\begin{pmatrix}-2\\4\end{pmatrix}, \vec{CF} =\begin{pmatrix}-2\\1\end{pmatrix}, \vec{DE} =\begin{pmatrix}0\\4\end{pmatrix}, \vec{DF} =\begin{pmatrix}0\\1\end{pmatrix})$

, et les coordonnées des points sont .

2. Le vecteur $\vec{EF}$ est donné par $\vec{EF} = \vec{CF} - \vec{CE} =\begin{pmatrix}0\\-3\end{pmatrix}$ .

Le vecteur $\vec{DG}$ est donné par $\vec{AB} - \vec{AD} - \vec{DG} = \begin{pmatrix}8\\0\end{pmatrix} - \begin{pmatrix}0\\4\end{pmatrix} - \vec{DG} =\begin{pmatrix}8\\-4\end{pmatrix} - \vec{DG}$ , d’où $\vec{DG} =\begin{pmatrix}-2\\4\end{pmatrix}$ .

Ainsi, $\vec{EF}.\vec{DG} = 0\times (-2) + (-3)\times 4 = -12$ .

3. Le produit scalaire $\vec{EF}.\vec{DG}$ est négatif, ce qui montre que les vecteurs $\vec{EF}$ et $\vec{DG}$ ne sont pas orthogonaux, et donc que les droites (EF) et (DG) ne sont pas perpendiculaires.

EXERCICE 9 :

a) On a $\vec{BA} = -\vec{AB}$ et $\vec{BF} = \frac{1}{2}\vec{BA}$

donc $\vec{BA}.\vec{BF} = -\frac{1}{2}||\vec{BA}||^2 = -\frac{1}{2}AB^2$

b) On a $\vec{CF} = \frac{1}{2}\vec{CD}$

et donc $\vec{CF}.\vec{CD} = \frac{1}{2}||\vec{CD}||^2 = \frac{1}{2}CD^2 = \frac{1}{2}AB^2$

c) On a $\vec{AF} = \vec{AB}+\vec{BF}$

et donc $\vec{AF}.\vec{AB} = \vec{AB}^2 + \vec{AB}.\vec{BF} = AB^2 + \frac{1}{2}AB^2 = \frac{3}{2}AB^2$

d) On a $\vec{BE} = -\vec{BA}+\vec{BC} = -\vec{BA}$

et donc $\vec{AB}.\vec{BE} = -||\vec{AB}||^2 = -AB^2$

EXERCICE 10 :

a) $\vec{u}.\vec{v} = 2\times (-3)+1\times (-1) = -7$

b) $\vec{w}.\vec{v} = 1\times (-3)+4\times (-1) = -7$

c) $\vec{u}.(\vec{v}+\vec{w}) = \vec{u}.\vec{v}+\vec{u}.\vec{w} = -7-2 = -9$

d) $(-2\vec{u}).\vec{v}+3(\vec{v}.\vec{w}) = -4\times (-7)+3((-3)\times (1)+(-1)\times (4)) = 28-15 = 13$

EXERCICE 11 :

On a $\vec{u}.\vec{v} = (-3)\times (-8)+4\times (-6) = 24-24 = 0$

donc les vecteurs $\vec{u}$ et $\vec{v}$ sont orthogonaux.

EXERCICE 12 :

a) Un vecteur directeur de (d_1) est $\vec{u}_1 = (3;2)$ et un vecteur directeur de (d_2) est $\vec{u}_2 = (-2;3)$ .

On a $\vec{u}_1.\vec{u}_2 = 3\times (-2)+2\times 3 = 0$ donc les droites (d_1) et d2 sont perpendiculaires.

b) Un vecteur directeur de (d_1) est $\vec{u}_1 = (1;1)$ et un vecteur directeur de (d_2) est $\vec{u}_2 = (-1;1)$ .

On a $\vec{u}_1.\vec{u}_2 = 1\times (-1)+1\times 1 = 0$ donc les droites (d_1) et (d_2) sont perpendiculaires.

c) Un vecteur directeur de la droite (d_1) est $\vec{u}_1 = (-1;3)$ .

On a $\vec{u}_1.\vec{u}_2 = (-1)\times (-1)+3\times 3 = 1 \neq 0$ donc les droites (d_1) et (d_2) ne sont pas perpendiculaires.

EXERCICE 13 :

a) $\vec{u}.\vec{v} = (-2)\times (-1)+3\times (-5) = 1-15 = -14$

b) $(4\vec{u}).\vec{v} = 4(-2)\times (-1)+4\times 3\times (-5) = 8-60 = -52$

c) $(\vec{u}-\vec{v}).(\vec{u}+\vec{v}) = (\vec{u}.\vec{u}-\vec{v}.\vec{v}) = (||\vec{u}||^2-||\vec{v}||^2) = (4+9)-(1+25) = -13$

EXERCICE 14 :

On a $\vec{u}.\vec{v} = (-3)\times (-8)+4\times (-6) = 24-24 = 0$ donc les vecteurs $\vec{u}$ et $\vec{v}$ sont orthogonaux.

2. On a $\vec{AB} = (1-(-3);3-(-2)) = (4;5)$ et $\vec{u} = (-5;4)$ .

On a $\vec{AB}.\vec{u} = 4\times (-5)+5\times 4 = -20+20 = 0$ donc les vecteurs $\vec{AB}$ et $\vec{u}$ sont orthogonaux.

EXERCICE 15 :

1. On utilise la loi des cosinus : $BC^2 = AB^2+AC^2-2\times AB\times AC\times \cos(\widehat{BAC}) = 9+16+12 = 37$ donc $BC = \sqrt{37}$

2. On utilise la loi des cosinus : $MP^2 = MN^2+NP^2-2\times MN\times NP\times \cos(\widehat{MNP}) = 25+49-70\times \cos(61^\circ) \approx 23,1$

donc $MP \approx \sqrt{23,1}$

3. On utilise la loi des cosinus :

$\cos(\widehat{EFG}) = \frac{EF^2+FG^2-EG^2}{2\times EF\times FG} = \frac{49+36-121}{2\times 7\times 6} = -\frac{1}{12} \\donc\\\\ \widehat{EFG} \approx 103 , 6^\circ$

4. On utilise la loi des cosinus :

$\cos(\widehat{EDF}) = \frac{EF^2+DF^2-ED^2}{2\times EF\times DF} = \frac{25+64-81}{2\times 5\times 8} = \frac{1}{8}\\\\ donc \\\\\widehat{EDF} \approx 82{,}5^\circ$

EXERCICE 16 :

a) On a $\vec{u}.(\vec{u}+\vec{v}) = \vec{u}.\vec{u}+\vec{u}.\vec{v} = a^2$

b) On a $(2\vec{u}-3\vec{v}).\vec{v} = 2\vec{u}.\vec{v}-3\vec{v}.\vec{v} = -3b^2$

c) On a $(\vec{u}+\vec{v})^2 = \vec{u}^2+2\vec{u}.\vec{v}+\vec{v}^2 = a^2+b^2$

EXERCICE 17 :

On a $\vec{v} = 3\vec{u}$ donc $\vec{u}.\vec{v} = 3a^2$ .

Les vecteurs $\vec{u}$ et $\vec{w}$ sont orthogonaux donc $\vec{u}.\vec{w} = 0$ .

On a $\vec{u}+\vec{w} = (\vec{u}+\vec{v})+(\vec{w}-\vec{v}) = \frac{a}{\sqrt{10}}\times (3\vec{u}+\vec{w})-\frac{3a}{\sqrt{10}}\times \vec{v}$

donc $(\vec{u}+\vec{v}).(\vec{u}+\vec{w}) = \frac{a^2}{10}(3a^2)+0 = \frac{3}{10}a^4$ .

On a $(\vec{u}+\vec{w})^2 = \vec{u}^2+2\vec{u}.\vec{w}+\vec{w}^2 = a^2+121a^2 = 122a^2$ .

EXERCICE 18 :

a) On a

$\vec{AB}.\vec{CD} = |\vec{AB}|\times |\vec{CD}|\times \cos(\widehat{AB,CD}) = AB\times DC\cos(\widehat{DC,AB}) = BA\times DC$

b) On a

$\vec{AB}.\vec{CD}+\vec{AB}.\vec{CE} = \vec{AB}.(\vec{CD}+\vec{CE}) = \vec{AB}.\vec{DE} = \vec{AB}.\vec{ED} = \vec{AB}.\vec{EC}+\vec{AB}.\vec{CD}$

c) On a

$\vec{AB}.\vec{AC} = AB\times AC\cos(\widehat{AB,AC}) = AB\times AC\cos(\widehat{BAC}-\widehat{CAB}) = AB(AB-BC) = AB^2-BA\times BC$

EXERCICE 19 :

1. Soit M un point du plan. On a $\vec{MA}+\vec{MB} = \vec{AB}$

donc

$(\vec{MA}+\vec{MB})^2 = \vec{AB}^2 = 144$

ce qui donne

$\vec{MA}^2+2\vec{MA}.\vec{MB}+\vec{MB}^2 = 144$ .

Comme I est le milieu de [AB], on a $\vec{MA}=\vec{MI}-\vec{AI}$ et $\vec{MB} = \vec{MB}-\vec{AI}$ .

En injectant ces expressions dans l’équation précédente, on obtient

$\vec{MI}.\vec{AI}+\vec{MI}.\vec{BI}+\vec{BI}.\vec{AI} = 68$ .

Posons $\vec{MI} = (x;y)$ et $\vec{AI} = (-\frac{1}{2};0)$ .

On a alors $\vec{BI} = (x+\frac{1}{2};y)$ et donc $\vec{MI}.\vec{AI} = -\frac{x}{2}$ .

En injectant ces expressions dans l’équation précédente et en développant, on obtient l’équation suivante :

$-\frac{x}{2}+2(x+\frac{1}{2})y+4y^2 = 68$ .

Ce qui donne l’équation suivante pour y : .

Cette équation admet des solutions réelles si et seulement si le discriminant est positif, ce qui donne $x^2\geq\, 31$ .

Ainsi, l’ensemble des points M qui vérifient l’équation est l’ensemble des points situés à l’extérieur ou sur le cercle de centre I et de rayon $\sqrt{31}$ .

2. Soit M un point du plan.

On a $\vec{MC}+\vec{MD} = \vec{CD} = \sqrt{100} = 10$

donc

$(\vec{MC}+\vec{MD})^2 = \vec{CD}^2 = 100$ ce qui donne $\vec{MC}^2+2\vec{MC}.\vec{MD}+\vec{MD}^2 = 100$ .

Comme H est le milieu de [CD], on a $\vec{MC}=\vec{MH}-\vec{CH}$ et $\vec{MD} = \vec{MD}-\vec{DH}$ .

En injectant ces expressions dans l’équation précédente, on obtient $\vec{MH}.\vec{CH}+\vec{MH}.\vec{DH}+\vec{CH}.\vec{DH} = -49$ .

Posons $\vec{MH} = (x;y)$ et $\vec{CH} = (5;0)$ .

On a alors $\vec{DH} = (x-5;y-10)$ et donc $\vec{MH}.\vec{CH} = 5x$ .

En injectant ces expressions dans l’équation précédente et en développant, on obtient l’équation suivante : .

Ainsi, l’ensemble des points M qui vérifient l’équation est la droite passant par H et parallèle à la droite (CD).

EXERCICE 20 :

On a $\vec{AB} = (1;a)$ et $\vec{AC} = (-a;1)$ .

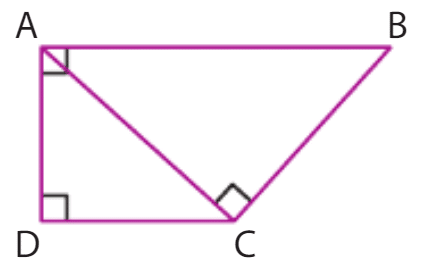
On a $\vec{AB}.\vec{AC} = -a+a = 0$ .

D’un autre côté, on a donc les triangles ABD et BCD sont rectangles en B et C respectivement et $AC^2 = AB^2+BC^2 = AB\times CD$ .

Voir Corrigés 11 à 20...

EXERCICE 21 :

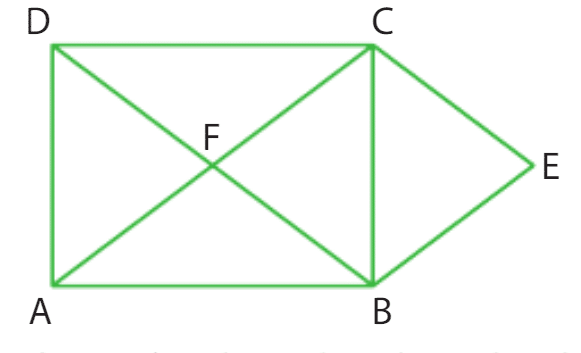
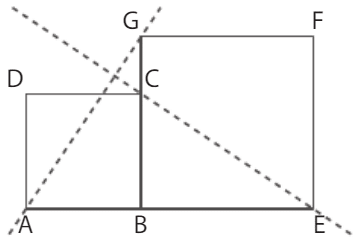
A. Avec coordonnées
1. Les coordonnées des points sont : ,

donc il suffit de trouver les coordonnées du point G.

Le vecteur $\vec{GB}$ est égal à $\vec{GE}+\vec{EA}+\vec{AB} = (-a+1,a)+(0,a)+(1,0) = (2-a,2a)$

donc les coordonnées de G sont (2-a,a) .
2. Les droites (AG) et (CE) sont perpendiculaires si et seulement si $\vec{AG}.\vec{CE} = 0$ .

On a $\vec{AG} = (-a+1,a)$ et $\vec{CE} = (-a,a-1)$

donc $\vec{AG}.\vec{CE} = -a(a-1)+(a)(a-1) = 0$ .

B. Sans coordonnées
1. On a

$(\vec{AB}+\vec{BG}).(\vec{CB}+\vec{BE}) \\\\= \vec{AB}.\vec{CB}+\vec{AB}.\vec{BE}+\vec{BG}.\vec{CB}+\vec{BG}.\vec{BE} \\\\= \vec{AB}.\vec{CB}+\vec{BG}.\vec{BE}+\vec{AB}.\vec{BE}+\vec{BG}.\vec{CB}$ .

Comme les vecteurs $\vec{AB}$ et $\vec{CB}$ sont orthogonaux et de même norme, on a $\vec{AB}.\vec{CB} = \vec{CB}^2-\vec{BQ}^2 = (a-1)^2+a^2 = 2a^2-2a+2$ .

De même, on a $\vec{BG}.\vec{BE} = \vec{BE}^2-\vec{BQ}^2 = (a^2+1)-a^2 = 1$ .

Il reste donc à calculer les produits scalaires $\vec{AB}.\vec{BE}$ et $\vec{BG}.\vec{CB}$ .

On a $\vec{AB}.\vec{BE} = \vec{AB}.\vec{BC}-\vec{EC}.\vec{AB} = -a+1$

et $\vec{BG}.\vec{CB} = \vec{BG}.\vec{BC}-\vec{CG}.\vec{BG} = a+1$ .

En injectant ces calculs dans l’expression précédente, on obtient ce qui donne a = 0.

Ainsi, les droites (AG) et (CE) sont perpendiculaires.

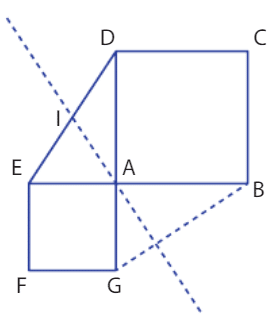
EXERCICE 22 :

A. Sans coordonnées
1. On a $AD+AE = a\sqrt{2}+a = 2a\frac{\sqrt{2}}{2}+2a\frac{\sqrt{2}}{2}+\sqrt{2}a = 2Al$ .
2. On a

$(AD+AE).(AB+AG) = AD.AB+AD.AG+AE.AB+AE.AG = a^2+(a+a)\times (-a)+(a+a)\times (a)+(a+a)\times (0) = 0$ .

Donc les droites (AI) et (BG) sont perpendiculaires.

B. Avec coordonnées
1. On a A(0,0), $I(-\frac{a}{2},\frac{a}{2}), B(a,0)$ et $G(2a,\frac{a}{2})$ .
2. Les vecteurs $\vec{AI} = (-\frac{a}{2},\frac{a}{2})$ et $\vec{BG} = (a,\frac{a}{2})$ sont-ils orthogonaux ?

On a $\vec{AI}.\vec{BG} = -\frac{a^2}{2}+a\frac{a}{2} = \frac{a^2}{2} \neq 0$ , donc les droites ne sont pas orthogonales.

Avec les coordonnées, on peut également calculer les équations des droites (AI) et (BG) et vérifier qu’elles sont perpendiculaires (on peut utiliser la méthode des coefficients directeurs).

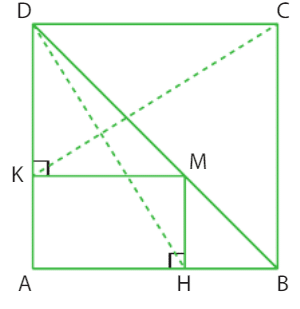
EXERCICE 23 :

1.
a) On utilise le repère (A;B,D) et on note (x;y) les coordonnées de M.

Les coordonnées de H sont (x,0) et les coordonnées de K sont (0,y).

Les coordonnées de C sont $(\frac{y}{2},\frac{y}{2})$ car AC est la diagonale du carré.

Les coordonnées de D sont $(\frac{1-x}{2},\frac{1-x}{2})$ .

Les vecteurs CK et DH sont alors respectivement $(\frac{y}{2},\frac{y}{2})-(0,y) = (\frac{y}{2},-\frac{y}{2})$ et $(\frac{x}{2},-\frac{x}{2})-(x,0) = (-\frac{x}{2},-\frac{x}{2})$ et leur produit scalaire vaut $-\frac{xy}{2}+\frac{xy}{2}=0$ , donc les droites (CK) et (DH) sont perpendiculaires.
b) On a $\vec{BK} = (0,y)$ et $\vec{DH} = (x,0)-(x,y)\times \frac{(0,1).(x,y)}{\|(x,y)\|^2} = (x,\frac{x^2-y^2}{x^2+y^2})$

et $\vec{CK} = (\frac{y}{2},\frac{y}{2})-(0,y)\times \frac{(1,0).(0,y)}{\|(\frac{y}{2},y)\|^2} = (\frac{y^2}{2y^2+1},\frac{y^2}{2y^2+1})-\frac{1}{y^2+\frac{1}{4}}(0,y) = (\frac{2y^2}{2y^2+1},\frac{y}{2y^2+1)}$ .

On a donc $\vec{CK}.\vec{DH} = \frac{2xy^2}{(2y^2+1)^2}-\frac{xy^2}{(x^2+y^2)(2y^2+1)}-\frac{xy^2}{(x^2+y^2)(2y^2+1)}+\frac{y^3}{(x^2+y^2)(2y^2+1)} = \frac{-xy(x^2-y^2)}{(x^2+y^2)(2y^2+1)} = 0$

donc les droites (CK) et (DH) sont perpendiculaires.

2.
a) On utilise le repère (A;B,D) et on note (x;y) les coordonnées de M. Les coordonnées de H sont (x,0) et les coordonnées de K sont (0,y) .

Pour démontrer que les longueurs DH et CK sont égales, on calcule les coordonnées de leur milieu et on montre qu’elles sont égales. Les coordonnées du milieu de DH sont $(\frac{x}{2},-\frac{x}{2})$ et les coordonnées du milieu de CK sont $(\frac{y^2}{2y^2+1},\frac{y}{2y^2+1})$ .

On a donc à montrer que $\frac{x}{2}=\frac{y^2}{2y^2+1}$ et $-\frac{x}{2}=\frac{y}{2y^2+1}$ , ce qui est vérifié en remplaçant y par $\frac{\sqrt{2}}{2}$ et en utilisant le fait que $x = 1-\frac{\sqrt{2}}{2}y$ .
b) On peut également utiliser la géométrie pour démontrer que DH et CK ont même longueur. On remarque que les triangles DMH et DCK sont semblables, donc $\frac{DH}{CK}=\frac{HM}{CK}=\frac{CK}{CM}=\frac{CK}{CD}=\frac{1}{\sqrt{2}}$ . De plus, les triangles DHC et CKM sont semblables, donc $\frac{CD}{CK}=\frac{DH}{CM}=\sqrt{2}$ , donc DH=CK.

Voir Corrigés 21 à 23...

Télécharger puis imprimer cette fiche en PDF.

Télécharger ou imprimer cette fiche «corrigé des exercices sur le produit scalaire en 1ère.» au format PDF afin de pouvoir travailler en totale autonomie.