Corrigé des exercices sur les fractions, inéquations en 2de.

EXERCICE 1 :

ÉTAPE 1:

1. Dans l’exercice 1, nous devons mettre les nombres donnés sous forme irréductible et montrer les calculs.
2. Dans l’exercice 2, nous devons mettre les nombres donnés sous forme scientifique.

$a=\frac{1+\frac{2}{5}}{3-\frac{7}{5}}=\frac{ \frac{5}{5}+\frac{2}{5}}{\frac{15}{5}-\frac{7}{5}}=\frac{ \frac{7}{5}}{\frac{8}{5}}= \frac{7}{5}\times \frac{5}{8}=\frac{7}{8}$
Forme décimale :
0,875

ÉTAPE 2:

1. Pour l’exercice 1, j’ai l’expression pour a : $a = \frac{7}{8}$ .
2. Je peux maintenant passer au calcul de b et c.

$b=\frac{3^7\times (2^{-3})^5\times 6^4}{(3^2)^5\times (2^{-5})^2}=$

Résultat :
$\frac{3}{2}$
Forme décimale :
1,5

ÉTAPE 3:

1. Pour l’exercice 1, j’ai l’expression pour b : b = $\frac{3}{2}$ .
2. Je peux maintenant passer au calcul de c.

$c=\frac{10^4 \times 15^2}{(2^3)^2 \times 12^3}$ =

Résultat exact :
$\frac{15625}{768}$
Approximation décimale :
20.34505208333…

ÉTAPE 4:

1. Pour l’exercice 1, j’ai l’expression pour c : $c =\frac{ 15625}{768}$ .
2. Nous pouvons passer à l’exercice 2.

$a=\frac{13}{25}\times 10^9=$

Résultat :
a = 520000000

ÉTAPE 5 :

1. Pour l’exercice 2, j’ai l’expression pour a : a = 520000000.
2. Je peux maintenant passer au calcul de b.

$b=\frac{4195}{125}\times 10^{-5}=$

Résultat :
$b = \frac{839}{2500000}$

ÉTAPE 6 :

1. Pour l’exercice 2, j’ai l’expression pour b : $b = \frac{839}{2500000}$ .
2. J’ai maintenant les réponses finales pour les deux exercices.

Réponse finale:
EXERCICE 1 :
a = $\frac{7}{8}$
b = $\frac{3}{2}$
$c = \frac{15625}{768}$

EXERCICE 2 :

$a=5,2 \times 10^8$

$b=3,356 \times 10^{-1}$

EXERCICE 3 :

Tout d’abord, rappelons que $\sqrt{81}=9$ car $9^2=81$, et que $\sqrt{242}$ ne peut pas être simplifié.

Nous pouvons donc simplifier la fraction $\dfrac{\sqrt{81}}{\sqrt{242}}$ : $\frac{\sqrt{81}}{\sqrt{242}} = \frac{9}{\sqrt{242}} = \frac{9}{2\sqrt{121}} = \frac{9}{22} \sqrt{121} = \frac{9}{22} \times 11 = \frac{99}{22}$

Ensuite, nous pouvons simplifier la racine carrée $\sqrt{\dfrac{98}{25}}$ :

$\sqrt{\frac{98}{25}} = \frac{\sqrt{98}}{\sqrt{25}} = \frac{\sqrt{2\cdot 49}}{5} = \frac{7\sqrt{2}}{5}$

Finalement, nous pouvons multiplier les deux résultats : $a = \frac{\sqrt{81}}{\sqrt{242}}\times \sqrt{\frac{98}{25}} = \frac{99}{22} \times \frac{7\sqrt{2}}{5}= \frac{693\sqrt{2}}{110} = \frac{63\sqrt{2}}{10}$

Nous ne pouvons pas simplifier davantage car et sont premiers entre eux.

EXERCICE 4 :

On commence par développer et simplifier l’équation :

$\begin{align*} 3(2-5x)+3+x-(1-2x) =5x+9 \\ 6-15x+3+x-1+2x =5x+9 \\ 10-12x =5x+9 \\ -12x-5x =9-10 \\ -17x =-1 \\ x =\frac{1}{17} \end{align*}$

La solution de cette équation dans $\mathbb{R}$ est donc $x=\frac{1}{17}$ .

On développe et on regroupe les termes pour obtenir une équation linéaire en $y$ :

$\begin{align*} 2x(3-5y)+5y =3x-2 \\ 6x-10xy+5y =3x-2 \\ (6x+5)+(10x-5)y =3x-2 \\ y =\frac{3x-2-5}{10x-5} \\ y =\frac{3x-7}{5(2x-1)} \end{align*}$

La valeur interdite pour est $x=\frac{1}{2}$ , car le dénominateur 2x-1 de la fraction devient alors nul.

EXERCICE 5 :

a) L’intervalle représentant l’ensemble des réels x satisfaisant à la condition -1 ≤ x ≤ 5 est [ -1 , 5 ].

b) L’intervalle représentant l’ensemble des réels x satisfaisant à la condition 3 < x ≤ 7 est ] 3 , 7 ].

c) L’intervalle représentant l’ensemble des réels x satisfaisant à la condition x ≥ 3 est [ 3 , +∞ [.

d) L’intervalle représentant l’ensemble des réels x satisfaisant à la condition x ≤ -5 est ] -∞ , -5 ].

a) Sur une droite graduée :

I = ]-∞ ; 4[ est représenté par la partie gauche de la droite, qui exclut 4 et contient tous les nombres à gauche de 4.

J = [1 ; 7] est représenté par un segment fermé de la droite allant de 1 à 7 inclus.

L’intersection de I et J est l’ensemble des nombres compris entre 1 et 4 exclus, soit ]1 ; 4[.

La réunion de I et J est l’ensemble des nombres inférieurs ou égaux à 7 et qui sont strictement à gauche de 4, soit ] -∞ ; 4 [ ∪ [1 ; 7].

b) Sur une droite graduée :

I = ]-7 ; -3] est représenté par un segment ouvert de la droite allant de -7 à -3 inclus.

J = ]-4 ; +∞[ est représenté par la partie droite de la droite, qui exclut -4 et contient tous les nombres à droite de -4.

L’intersection de I et J est l’ensemble des nombres compris entre -7 et -3 exclus, qui sont strictement à droite de -4, soit ]-4 ; -3[.

La réunion de I et J est l’ensemble des nombres qui sont inférieurs ou égaux à -3 ou qui sont strictement à droite de -4, soit ] -∞ ; -3] ∪ ]-4 ; +∞[.

EXERCICE 6 :

$A = \frac{1}{5}\times \frac{-4}{3}+\frac{7}{2}= \frac{-4}{15}+\frac{35}{10} = \frac{-4}{15}+\frac{105}{30}=\frac{-8}{30}+\frac{105}{30}=\frac{97}{30}$

$B = \frac{13}{7}+(-\frac{8}{7}):(-\frac{4}{5})=\frac{13}{7}+\frac{8}{7}\times \frac{5}{4}=\frac{13}{7}+\frac{10}{7}=\frac{23}{7}$

$C = (\frac{3}{2}+\frac{3}{5})(\frac{5}{4}-\frac{4}{3})=\frac{15}{10} \times \frac{5}{12} - \frac{12}{15} \times \frac{15}{20} = \frac{25}{24}-\frac{36}{60}=\frac{25}{24}-\frac{3}{5}=\frac{25}{24}-\frac{36}{60}=\frac{25}{24}-\frac{18}{24}=\frac{7}{24}$

$D = -\frac{3}{8}-\frac{5}{8}\times \frac{7}{9}=-\frac{3}{8}-\frac{35}{72}=-\frac{27}{72}-\frac{35}{72}=-\frac{62}{72}=-\frac{31}{36}$

EXERCICE 7 :

$A= \frac{\frac{3}{2}-\frac{1}{3}}{\frac{3}{4}+\frac{2}{3}} = \frac{\frac{7}{6}}{\frac{17}{12}}=\frac{7}{6}\times \frac{12}{17}=\frac{14}{17}$

$B= 2+\frac{\frac{2}{7}}{\frac{5}{14}} = 2+\frac{2}{7}\times \frac{14}{5}=2+\frac{4}{5}=\frac{14}{5}$

$C=-\frac{3}{14}-\frac{3}{\frac{7}{5}}+2 = -\frac{3}{14}-\frac{3\times 5}{7}+2=-\frac{3}{14}-\frac{15}{7}+2 =-\frac{3}{14}-\frac{30}{14}+2=-\frac{31}{7}$

$E=\frac{3-\frac{7}{5}}{1-\frac{9}{10}}= \frac{\frac{8}{5}}{\frac{1}{10}}=\frac{8}{5}\times 10 =\frac{16}{5}$

$F=\frac{7}{-8}+\frac{6}{4}-1= -\frac{7}{8}+\frac{3}{2}-1=-\frac{7}{8}+\frac{12}{8}-\frac{8}{8}=\frac{-3}{8}$

EXERCICE 8 :

$A=5\sqrt{2}+12\sqrt{2}-14\sqrt{2}=3\sqrt{2}$

$B=\sqrt{4}\sqrt{5}-12\sqrt{5}+\sqrt{5}= -11\sqrt{5}$

$C=2\sqrt{3}+5\sqrt{3}+24\sqrt{3}=31\sqrt{3}$

$D=15\sqrt{7}-2\sqrt{7}+\sqrt{7}=14\sqrt{7}$

EXERCICE 9 :

$A = \dfrac{\sqrt{2}}{2}(\sqrt{2}+\dfrac{1}{\sqrt{2}}) = \dfrac{\sqrt{2}}{2}(\sqrt{2}+\sqrt{2}) = \boxed{2}$

$B = \sqrt{18}(\sqrt{2}-\dfrac{\sqrt{18}}{18}) = \sqrt{3^2\cdot2}\left(\sqrt{2}-\dfrac{3\sqrt{2}}{3^2\cdot2}\right) \\B= \sqrt{3^2\cdot2}\left(\dfrac{3\sqrt{2}-3\sqrt{2}}{3^2\cdot2}\right)\\B = \boxed{0}$

$C = \sqrt{3}(2-5\sqrt{3}) = 2\sqrt{3}-5\sqrt{3}^2 = 2\sqrt{3}-45 = \boxed{-43}$

$D = 5\sqrt{2}(\sqrt{2}-7\sqrt{18}) = 5\sqrt{2}\sqrt{2}(1-7\sqrt{2^2\cdot3^2}) = 5\cdot2(-47) = \boxed{-470}$

$E = (\sqrt{6}+2)\sqrt{2} = \sqrt{6\cdot2}+2\sqrt{2} = \boxed{2\sqrt{3}+2\sqrt{2}}$

$F = 2\sqrt{12}(\sqrt{12}-\sqrt{3}+\sqrt{6})\\F = 2\sqrt{4\cdot3}\left(\sqrt{4\cdot3}-\sqrt{3}+\sqrt{2\cdot3}\right) \\F= 2\cdot2\sqrt{3}(2\sqrt{3}-\sqrt{3}+ \sqrt{6})\\F = 2\cdot2\sqrt{3}\cdot\sqrt{6}\\F = \boxed{4\sqrt{18}}$

EXERCICE 10 :

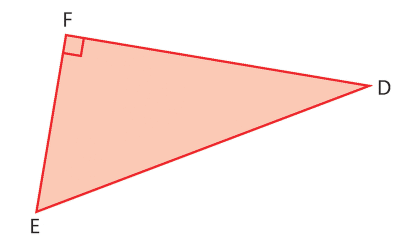
1. On utilise le théorème de Pythagore dans le triangle EDF :

$EF^2 = (5\sqrt{2})^2 + (3\sqrt{2})^2$

On simplifie en utilisant la racine carrée :

$EF = \sqrt{68} = \sqrt{4\times17} = 2\sqrt{17}$

Donc EF = $2\sqrt{17}$ cm.

2. Le périmètre du triangle EDF est la somme des longueurs des côtés :

$P = 5\sqrt{2} + 3\sqrt{2} + 2\sqrt{17}$
$P = (5+3)\sqrt{2} + 2\sqrt{17}$
$P = 8\sqrt{2} + 2\sqrt{17}$

On peut utiliser une calculatrice pour obtenir une valeur décimale approchée :

$P \approx 19,69$ cm

Donc le périmètre du triangle EDF arrondi au millimètre est de 19,7 cm.

EXERCICE 11 :

1. On peut simplifier $\sqrt{75}$ en $\sqrt{25}\cdot\sqrt{3}=5\sqrt{3}$ .

On a donc :
$5\sqrt{12}-\sqrt{75}=5\sqrt{4}\cdot\sqrt{3}-5\sqrt{3}=5\cdot 2\cdot \sqrt{3}-5\sqrt{3}=5\sqrt{3}.$
Donc a=5 et b=3

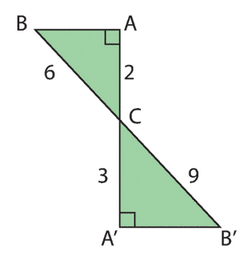
2. Les côtés opposés de ABCD sont parallèles et de même longueur, donc ABCD est un parallélogramme.

3. Le périmètre est la somme des longueurs des côtés de ABCD. Le côté AB mesure $5\sqrt{2}$ , le côté BC mesure 5 cm et le côté CD mesure 8 cm.

On a $DC=AB=5\sqrt{2}$ car ABCD est un parallélogramme.

Finalement, le périmètre est :
$P=AB+BC+CD+DA=5\sqrt{2}+5+8+5=5\sqrt{2}+18.$
L’arrondi au millimètre est donc $P\approx 27,28$ cm.

4. L’aire de ABCD est la base AB multipliée par la hauteur correspondante, qui est la distance entre les droites (AB) et (CD).

Cette distance est la longueur de la perpendiculaire issue de A sur (CD).

On peut construire cet orthogonal en traçant la droite (AE) telle que A soit le milieu de [CE].

On obtient alors un triangle rectangle AEC en A, rectangle en E.

La longueur de CE est $CD-DE=CD-\frac{BC}{2}=8-\frac{5}{2}=\frac{11}{2}$ cm.

On utilise ensuite le théorème de Pythagore dans AEC pour calculer la hauteur AE :
$(AE)^2=AC^2-EC^2=(AB+BC)^2-EC^2=(5\sqrt{2}+5)^2-\left(\frac{11}{2}\right)^2.$
On obtient $AE=\sqrt{503}$ cm.

Finalement, l’aire de ABCD est :
$A=AB\times AE=5\sqrt{2}\times \sqrt{503}=5\sqrt{1006}.$
L’aire exacte est donc $A=5\sqrt{1006}\,cm^2$ .

EXERCICE 12 :

On cherche un nombre de marches compris entre 130 et 150 qui est divisible par 3 et qui a un reste de 1 lorsqu’on le divise par 4.

Le plus petit multiple de 3 qui a un reste de 1 lorsqu’on le divise par 4 est 13 (car $3 \times 4 + 1 = 13$ ).

Le plus grand multiple de 3 qui est inférieur ou égal à 150 est 147.

Donc le nombre de marches de l’escalier est 147.

EXERCICE 13 :

1. On a $\frac{AB}{A'B'} = \frac{4\sqrt{2}}{3\sqrt{3}} \times \frac{\sqrt{3}}{\sqrt{3}} = \frac{4\sqrt{6}}{9}$ .

2. On a $\frac{4\sqrt{6}}{9} = \sqrt{\frac{16}{81} \times \frac{6}{1}} = \sqrt{\frac{64}{9} \times \frac{1}{6}} = \sqrt{\frac{32}{27}}$ .

3. On a $AB = 4\sqrt{2}$ et $AB' = 3\sqrt{3}$ .

4. On peut simplifier $\frac{\sqrt{32}}{\sqrt{72}}$ en factorisant le numérateur et le dénominateur par $\sqrt{2}$ .

On obtient alors

$\frac{\sqrt{32}}{\sqrt{72}} = \frac{\sqrt{2} \times \sqrt{16}}{\sqrt{2} \times \sqrt{36} \times \sqrt{2}} = \frac{4}{6\sqrt{2}} = \frac{2\sqrt{2}}{3}.$

On s’aperçoit alors que cette fraction est égale à $\frac{AB}{A'B'}$ trouvée à la question 1, donc $\frac{\sqrt{32}}{\sqrt{72}}$ peut être simplifié en $\frac{2\sqrt{2}}{3}$ .

Télécharger puis imprimer cette fiche en PDF.

Télécharger ou imprimer cette fiche «corrigé des exercices sur les fractions, puissances, inéquations et intervalles en 2de.» au format PDF afin de pouvoir travailler en totale autonomie.

Réviser les cours et exercices avec nos Q.C.M :

Q.C.M en 6ème Q.C.M en 5ème Q.C.M en 4ème Q.C.M en 3ème Q.C.M en 2de Q.C.M en 1ère Q.C.M en Terminale

Mathématiques Web c'est 2 266 319 fiches de cours et d'exercices téléchargées.

Corrigé des exercices sur les fractions, puissances, inéquations et intervalles en 2de.

Réviser les cours et exercices avec nos Q.C.M :

Cours et exercices similaires

Corrigé des exercices sur la géométrie dans l’espace en 2de.

Corrigé des exercices sur les systèmes de deux équations en 2de.

Corrigé des exercices sur les statistiques en 2de.

Vous devriez consulter :

Vecteurs et repères : exercices de maths en 2de corrigés en PDF.

Les fractions, puissances et racines carrées : exercices de maths en 2de corrigés en PDF.

Droites parallèles et perpendiculaires : exercices de maths en 6ème corrigés en PDF.

Les équations : exercices de maths en 3ème corrigés en PDF.