Les sections de volumes de l’ espace sont très importants en géométrie. Ainsi, avec un contrôle de maths sur les volumes et sections de volumes de l’espace en classe de troisième (3ème), vous pourrez progresser davantage.
Exercice n° 1:
On considère cône de sommet S et de base le disque de centre O.
Il est coupé par un plan P parallèle à la base ,on suppose que (OA) et (O’A’) sont parallèles.
Les rayons sont donnés ;OA= 12cm et OA’=4,8 cm.
La distance entre les points O et O’ est 9 cm.
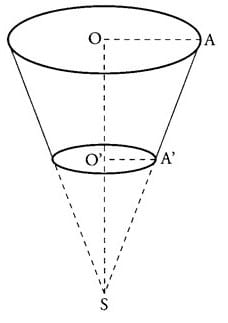
a) Calculer la mesure de l’angle à un degré près.
b) Montrer que .
c) Montrer que SO =15 cm
d) Calculer la valeur exacte du volume du cône de sommet S et de base le disque de centre O (en fonction de ).
e) Calculer le volume du cône de sommet S et de base le disque de centre O’.
En déduire le volume du tronc de cône à un près.
Exercice n° 2 : sections de volumes
On considère deux vases (voir figures ci-dessous) : l’un constitué d’une pyramide régulière et l’autre d’un cylindre de révolution et tous deux montés sur des supports (grisés sur la figure).
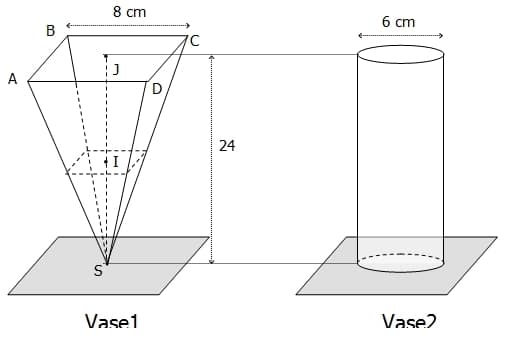
1. Quelle est la nature du quadrilatère ABCD ?
Calculer le volume V1 du vase 1 en puis en L.
2. On remplit le vase 1 jusqu’à mi-hauteur (I est le milieu de [SJ]), obtenant ainsi une « pyramide d’eau », réduction de la pyramide constituée par le vase.
a. Quelle est l’échelle de cette réduction ?
b. Par combien doit-on multiplier le volume du vase pour obtenir celui de l’eau ?
c. En déduire que le volume restant inoccupé représente les du volume initial V1.
3. On verse 512 d’eau dans le vase 2.
a. En notant V2 le volume du vase 2, justifier le fait que cela ne déborde pas.
b. Calculer, au dixième prés, la hauteur d’eau x en centimètre obtenue dans le vase 2.
Exercice n° 3 :
Une boîte en carton a la forme représentée ci-dessous :
- ABCDA’B’C’D’ est un cube de 6 cm d’arête ;
- SABCD est une pyramide régulière dont les quatre faces sont des triangles équilatéraux.
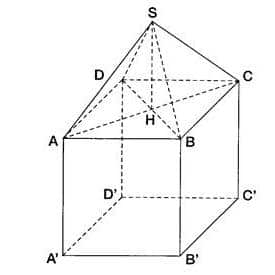
1. Calculer la longueur AC.
2. Démontrer que le triangle SAC est rectangle.
3. Calculer la hauteur SH de la pyramide SABCD.
Montrer que SH peut s’écrire .
4. Calculer le volume de la boîte arrondi au le plus proche.
Télécharger puis imprimer cette fiche en PDF.
Télécharger ou imprimer cette fiche «contrôle sur les sections de solides et volumes en troisième (3ème).» au format PDF afin de pouvoir travailler en totale autonomie.
D'autres cours et exercices à consulter
- Calcul littéral : contrôle de maths en troisième (3ème)
- Statistiques : contrôle de maths en 3ème à télécharger en PDF.
- Contrôle de trigonométrie en 3ème à imprimer en PDF.
- Généralités sur les fonctions : contrôle de maths en 3ème.
- Contrôle de maths sur les équations en 3ème à imprimer en PDF.
- Trigonométrie : contrôle de maths en 3ème (troisième ).
- Théorème de Thalès : contrôle de maths en 3ème à imprimer en PDF.
- Arithmétique : contrôle de maths en 3ème à imprimer en PDF.


