Un devoir surveillé de mathématiques sur le théorème de Thalès en troisième (3ème).
Ce contrôle de maths sur le théorème de Thalès est destiné aux enseignants, mais également aux élèves désireux de réviser un devoir surveillé de mathématiques sur le théorème de Thalès. A la fin de ce contrôle, vous devriez assimiler des compétences nouvelles. Utilisez les matériels nécessaires pour résoudre les exercices.
Exercice n° 1 :
Tracer un triangle ABC tel que :
AB = 6 cm, AC = 4,8 cm et BC = 8,4 cm
Sur [BA), placer le point E tel que BE = 11 cm.
Sur [CA), placer le point F tel que CF = 8,8 cm.
1) Calculer AE et AF.
2) Démontrer que (EF) // (BC).
3) Calculer la longueur du segment [EF] .
Exercice n° 2 :
Sur la figure, les droites (AG) et (RB) sont parallèles. L’unité de longueur est le centimètre.
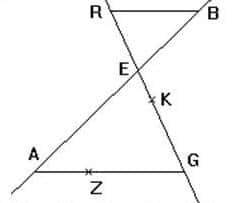
On a : BE = 3, AE = 5, AG = 10 et EG = 8.
1) Calculer les distances RB et RE.
2) On donne GK = 6,4 et GZ = 8.
Les droites (ZK) et (AE) sont-elles parallèles ?
Exercice n° 3 :
Sur la figure :
– Les droites (MK) et (OD) sont parallèles ;
– Les points E, S, M et O sont alignés dans cet ordre ;
– Les points F, S, K et D sont alignés dans cet ordre;
– SO = 6 ; SD = 10 ; SM = 4,8 ;SE = 2 et SF = 3.
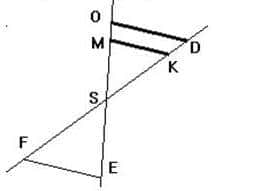
1) Calculer SK.
2) Les droites (EF) et (OD) sont-elles parallèles ?
Justifier.
Exercice n° 4 :
Sur la figure ci-dessous, on a :
(AB) // (IJ) et (BC) // (JK) ;
OA=3 cm ; OB=3,5 cm ; OC=2,5 cm et CK=1 cm.
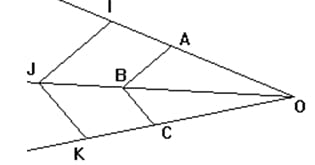
1) Calculer OJ, BJ, OI et IA.
2) Les droites (AC) et (IK) sont-elles parallèles ?
Justifier.
Télécharger puis imprimer cette fiche en PDF.
Télécharger ou imprimer cette fiche «théorème de Thalès : contrôle de maths en 3ème à imprimer en PDF.» au format PDF afin de pouvoir travailler en totale autonomie.
D'autres cours et exercices à consulter
- Contrôle sur les sections de solides et volumes en troisième (3ème).
- Généralités sur les fonctions : contrôle de maths en 3ème.
- Arithmétique : contrôle de maths en 3ème à imprimer en PDF.
- Contrôle de maths sur les équations en 3ème à imprimer en PDF.
- Contrôle de maths sur les statistiques en 3ème (troisième).
- Contrôle de maths sur les fonctions affines en 3ème.
- Contrôle de maths sur les fonctions linéaires en 3ème.
- Contrôle de trigonométrie en 3ème à imprimer en PDF.


