Les propriétés des cours sont toujours très importantes en géométrie. De plus, ce chapitre fait intervenir vos connaissances ainsi que vos compétences. Dans un triangle, si une droite passe par les milieux de deux côtés, alors on dit qu’elle est parallèle au troisième côté. Ensuite, la longueur du segment joignant les milieux de deux côtés est égale à la moitié de celle du troisième côté. Pour réussir ce contrôle, il faut rester bien concentré et utilisez tous les matériels nécessaires.
En outre, avant de commencer, lisez bien l’énoncé pour avoir un bon aperçu. Evitez toujours les erreurs de calcul lors de votre contrôle. A la fin de ce contrôle, vous devriez être capable de maîtriser toutes les notions de ce cours.
Exercice n° 1 : 4 points.
|
|
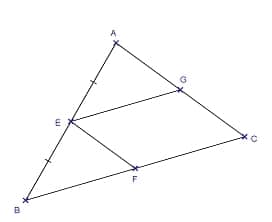
Les droites (EF) et (AC) sont parallèles.
On donne AC = 7 cm. 1. Démontrer que F est le milieu de [BC]. 2. Quelle est la longueur du segment [EF] ? (à justifier)
|
Exercice n° 2 : 6 points.
|
|
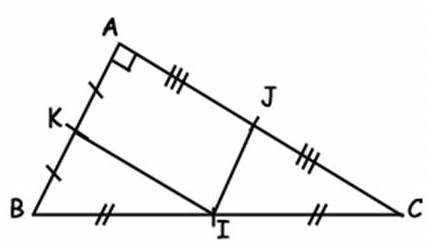
Montrer que AJIK est un rectangle.
|
Exercice n° 3 : 6 points.
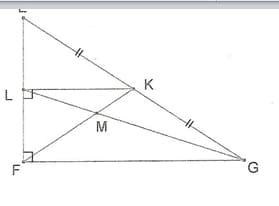
| EFG est un triangle rectangle en F K est le milieu du segment [EG]. La droite passant par K et perpendiculaire à (EF) coupe [EF] en L.1. a. Démontrer que les droites (LK) et (FG) sont parallèles. b. Démontrer que L est le milieu du segment [EF].2. Les droites (FK) et (GL) se coupent en M. Que représentent les droites (FK) et (GL) pour le triangle EFG ? En déduite que la droite (EM) coupe le segment [FG] en son milieu. |
|
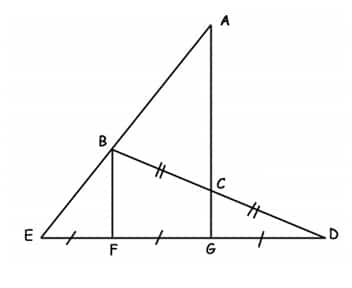
Exercice n° 4 : 4 points.
|
|
|
Télécharger puis imprimer cette fiche en PDF.
Télécharger ou imprimer cette fiche «contrôle sur la droite des milieux en quatrième (4ème)» au format PDF afin de pouvoir travailler en totale autonomie.
D'autres cours et exercices à consulter
- Contrôle sur le cosinus sur la trigonométrie en 4ème.
- Contrôle sur le calcul littéral de maths en 4ème (quatrième).
- Puissances : contrôle de maths en 4ème (quatrième ).
- Fractions : contrôle de maths en 4ème à télécharger en PDF.
- Proportionnalité : contrôle de maths en quatrième (4ème)
- Contrôle sur les équations en 4ème à télécharger en PDF.
- Contrôle de maths sur les statistiques en 4ème (quatrième).
- Nombres relatifs : contrôle de maths en 4ème à télécharger en PDF.