Un contrôle sur la symétrie centrale en maths est toujours essentiel pour les élèves en classe de cinquième (5ème). En effet, c’est un chapitre qui leur permet de développer des compétences nouvelles. De plus la symétrie centrale en maths nécessite une bonne maîtrise et de la concentration.
Exercice 1 : (2,5 pts)
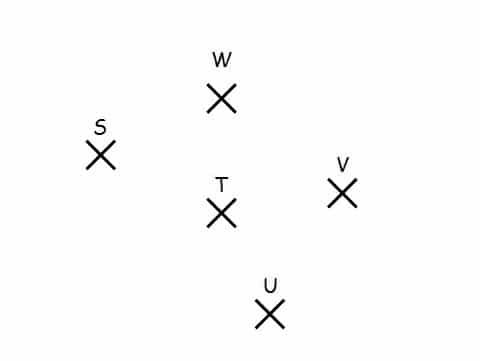
En laissant apparents les traits de construction, construire :
– S’ symétrique de S par rapport à T
– T’ symétrique de T par rapport à U
– U’ symétrique de U par rapport à V
– V’ symétrique de V par rapport à W
– W’ par rapport à S symétrique de W
Exercice 2 : (3 pts)
Sans l’aide d’aucune figure, compléter les phrases suivantes (symétrie centrale) :
è M’ est le symétrique de M par rapport à O signifie que le point …. est ………… du segment […. ….].
è C est le symétrique de B par rapport à A signifie que le point …. est ………….. du segment […. ….].
Exercice 3 : (6 pts) ‘symétrie centrale maths’
1. En laissant apparents les traits de construction, construire le symétrique de la figure par rapport à I :
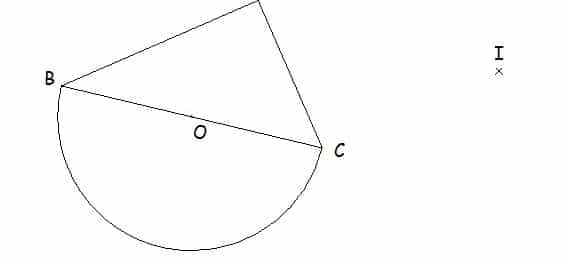
2. Citer 2 droites parallèles (à justifier) .
3. Citer 2 segments de même longueur (à justifier) .
Exercice 4 : (8,5 pts) ‘symétrie centrale maths ‘
1. Construire un triangle ABD tel que : AB = BD = 4 cm et = 90°.
Construire le cercle C de diamètre [AB] et de centre C.
2. Construire les points P, J et L symétriques des points B, C et A par rapport à D.
3. Tracer le symétrique du cercle C par rapport au point D. Quel est son centre ? Quel est son rayon ?
4. Combien mesure le segment [PL] ? Justifier la réponse par une propriété du cours.
5. Pourquoi la droite (PJ) est-elle perpendiculaire à la droite (BD) ? Justifier la réponse par une propriété du cours.
6.Compléter :
Quel est le symétrique du point B par rapport à D ?
Quel est le symétrique du point L par rapport à D ?
Que peut-on déduire pour les droites (BL) et (PA) ? Justifier la réponse par une propriété du cours.
Télécharger ou imprimer cette fiche «contrôle sur la symétrie centrale de maths en 5ème (cinquième).» au format PDF afin de pouvoir travailler en totale autonomie.
D'autres cours et exercices à consulter
- Contrôle de maths sur les fractions en 5ème (cinquième).
- Devoir en commun de maths en 5ème à télécharger en PDF.
- Devoir en commun de maths en cinquième (5ème).
- Contrôle sur le calcul littéral en maths en 5ème à télécharger en PDF.
- Contrôle sur les nombres relatifs en 5ème à télécharger en PDF.
- Contrôle sur la proportionnalité en maths cinquième (5ème)
- Contrôle sur le parallélogramme de maths en 5ème (cinquième ).
- Aires de figures : contrôle de maths en 5ème à imprimer en PDF.

