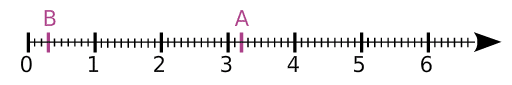I. Sous-multiples de l’unité
1.Les dixièmes
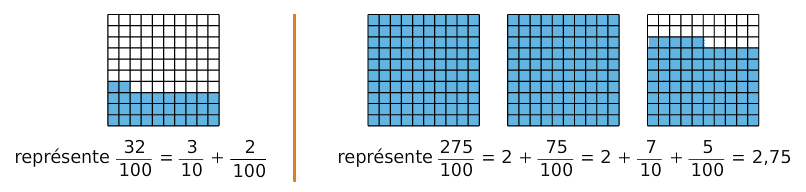
Lorsque l’on décompose une unité en dix parties égales, on obtient des dixièmes.
Un dixième se note .
Dans l’unité, il y a dix dixièmes donc .
Exemple :
2. Les centièmes
Lorsque l’on décompose une unité en cent parties égales, on obtient un centième.
Un centième se note .
Dans l’unité, il y a cent centièmes donc .
Exemple :
3.Les millièmes
Lorsque l’on décompose une unité en mille parties égales, on obtient des millièmes.
Un millième se note .
Dans l’unité il y a mille millième donc .
Exemple :
II. Décomposition et nom des chiffres
Tout nombre pouvant s’écrire sous la forme d’une fraction décimale, c’est à dire dont le numérateur est un nombre entier et le dénominateur est 1,10,100,1 000,10 000 …, est un nombre décimal.
Il peut aussi se noter en utilisant une virgule, c’est son écriture décimale : elle est composée
d’une partie entière et d’une partie décimale.
Remarque :
Un nombre décimal a une partie décimale finie.
Exemple :
On considère le nombre décimal 1 345,824.
- Ce nombre se lit mille-trois-cent-quarante-cinq unités et huit-cent-vingt-quatre-unités.
- Il peut se décomposer sous la forme
- Voici le nom de chaque chiffre :
- 1 est le chiffre des milliers
- 3 est le chiffre des centaines
- 4 est le chiffre des dizaines
- 5 est le chiffre des unités
- 8 est le chiffre des dixièmes
- 2 est le chiffre des centièmes
- 4 est le chiffre des millièmes.
Remarque :
Un nombre entier est un nombre décimal particulier.
En effet, 25 peut s’écrire avec une virgule 25=25,0 ou sous la forme d’une fraction décimale .
III. Repérage sur une demi-droite graduée
Exemple :
Quelles sont les abscisses des points A et B?
Une unité est divisée en dix parts égales, ce qui signifie qu’elle est partagée en dix-dixièmes.
Le point A se trouve 2 dixièmes après 3. Donc son abscisse est .
Le point B a pour abscisse .
On note A(3,2) et B(0,3).
IV. Comparaison et rangement
1.Comparaison de deux nombres décimaux
Comparer deux nombres, c’est trouver qui est le plus grand, ou le plus petit, ou dire si ils sont égaux.
Remarque :
On utilise les symboles > pour « plus grand que » et < pour « plus petit que ».
Pour comparer deux nombres décimaux écrits sous forme décimale :
- on compare les parties entières;
- si les parties entières sont égales, alors on compare les chiffres de dixièmes;
- ils sont égaux, donc on compare les chiffres des centièmes;
- ils sont égaux, donc on compare les chiffres des millièmes;
- et ainsi de suite jusqu’à ce que les deux nombres aient des chiffres différents.
Exemple :
Comparer les nombres 81,357 et 81,36.
- On compare d’abord les parties entières des deux nombres;
- elles sont égales, donc on compare les chiffres des dixièmes;
- ils sont égaux, donc on compare les chiffres des centièmes.
- 5<6 donc 81,357<81,36.
Remarque :
Quand les parties entières sont égales, on peut comparer les parties décimales.
et
.
Or, 360 millièmes est plus grand que 357 millièmes donc 81,36>81,357.
2.Rangement de deux nombres décimaux
Exemple :
Ranger les nombres dans l’ordre croissant.
On repère le plus petit, puis le plus petit des nombres qui restent, et ainsi de suite jusqu’au dernier.
On obtient donc .
Avez-vous assimilé le cours sur les nombres décimaux en 6ème ?
QCM de maths en 6ème sur les nombres décimaux.