Proportionnalité et pourcentages : cours de maths en 6ème en PDF.
I. Tableaux de proportionnalité
1.Coefficient de proportionnalité
Exemple :
Au marché, le raison est vendu 3,50€ le kilogramme.
Pour 4 kg, on paie 4 fois plus que pour 1 kg, c’est-à-dire 14 €.
En effet, €.
Pour 0,50 kg, on paie deux fois moins que pour 1 kg, c’est-à-dire 1,75 €.
En effet, €.
On dit que le prix, en euros, est proportionnel à la masse, en kilogrammes.
On obtient le prix (en euros) en multipliant la masse (en kilogrammes) par 3,5.
Remarque :
Dans le tableau ci-dessus, on passe d’un nombre de la première ligne au nombre correspondant
de la deuxième ligne en multipliant par le même nombre.
On dit que ce nombre (3,5) est un coefficient de proportionnalité ( il s’agit du prix d’un kilogramme de raisins).
2.Multiplication d’une quantité par un nombre
Exemple 1 :
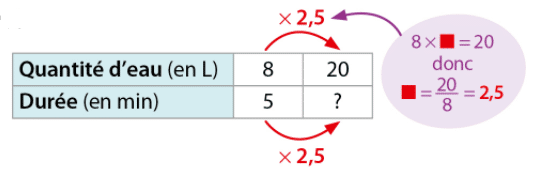
Le débit d’un robinet est régulier, c’est-à-dire que le nombre de litres qui s’écoulent est proportionnel à la durée d’écoulement. En 5 min, il s’écoule 8 litres d’eau.
En combien de temps s’écoulera-t-il 20 L d’eau ?
Donc il s’écoulera 20 L d’eau du robinet en 12,5 min.
Exemple 2 :
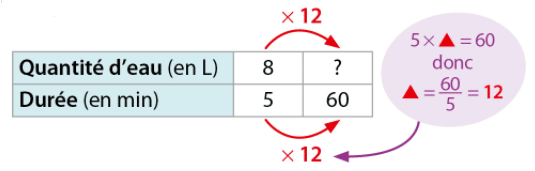
On reprend l’exemple 1 ci-dessus. En 5 min, il s’écoule 8 L d’eau.
Si on laisse le robinet ouvert 60 min, combien de litres d’eau s’écouleront ?
Donc en 60 min, il s’écoulera 96 L d’eau.
3.Additivité de la proportionnalité
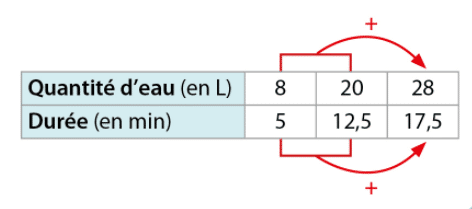
Exemple :
On reprend l’exemple 1 du paragraphe 2.En 5 min, il s’écoule 8 L et en 12,5 min, il s’écoule 20 L.
min et
L.
Donc en 17,5 min, il s’écoulera 28 litres d’eau.
II. Passage par l’unité et pourcentage
1.Passage par l’unité
Exemple :
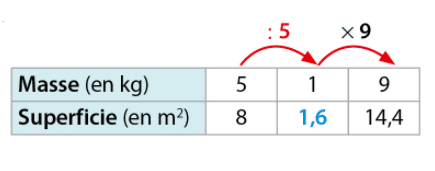
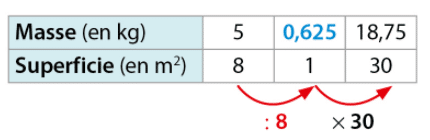
Avec 5 kg de peinture, on peut recouvrir 8 m² de façade.
- Pour calculer la superficie de façade recouverte avec 9 kg de peinture, on peut procéder ainsi :
– avec 1 kg de peinture, on peut recouvrir 8 m²: 5 c’est-à-dire 1,6 m².
– avec 9 kg de peinture, on peut recouvrir .
- Pour calculer la masse de peinture nécessaire pour 30 m² de façade, on peut procéder ainsi :
-pour 1m², il faut 5 kg : 8 c’est-à-dire 0,625 kg de peinture.
– pour 30 m², il faut .
On peut aussi utiliser ce tableau de proportionnalité :
2.Appliquer un taux de pourcentage
t désigne un nombre. Prendre t % d’une quantité, c’est multiplier cette quantité par .
Exemple :
Un yaourt de 125 g contient 14% de fruits.
Calculer la masse de fruits dans ce yaourt, c’est prendre 14% de 125 g, c’est-à-dire prendre
.
Donc il y a 17,5 g de fruits dans ce yaourt de 125 g.
- Prendre 50 % d’une quantité, c’est prendre la moitié.
- Prendre 25 % d’une quantité, c’est prendre le quart.
- Prendre 75 % d’une quantité, c’est prendre les trois-quarts.
Exemple :
25 % des 28 élèves d’une classe de 6° portent des lunettes.
donc 7 élèves de cette classe portent des lunettes.
Avez-vous assimilé ce cours sur la proportionnalité et les pourcentages en 6ème ?
QCM de maths sur la proportionnalité et les pourcentages en 6ème.
