Nombres complexes : cours de maths en terminale en PDF.

Les nombres complexes à travers un cours de maths en terminale complet et à assimiler

Cette leçon fait intervenir les notions suivantes :

définition du nombre complexe;
forme algébrique;
forme géométrique;
formule d’Euler;
formule de Moivre;
équations complexes;
représentation géométrique d’un nombre complexe;
partie réelle et imaginaire d’un nombre complexe;
opérations sur les nombres complexes.

I.Forme algébrique d’un nombre complexe

Théorème et définition :

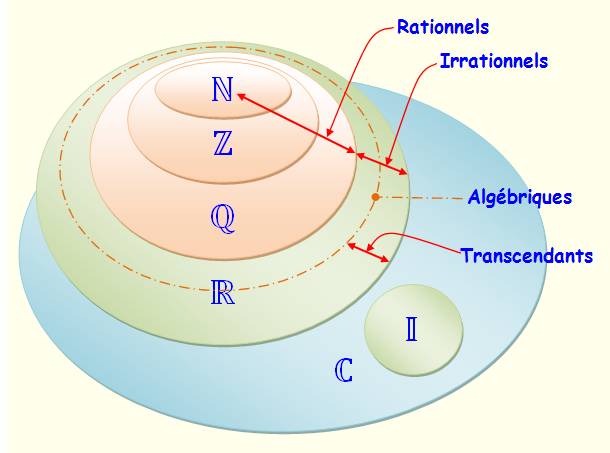
Il existe un ensemble de nombres noté $\mathbb{C}$ , dont les éléments sont appelés les nombres complexes, tel que :

$\mathbb{C}$ contient l’ensemble $\mathbb{R}$ des nombres réels;
les règles de calculs dans $\mathbb{C}$ sont les mêmes que dans $\mathbb{R}$ ;
$\mathbb{C}$ contient un élément noté $i$ tel que $i^2=-1$ ;
tout nombre complexe z peut s’écrire de manière unique sous la forme $z=x+iy$ avec $x$ et $y$ deux nombres réels (cette écriture s’appelle l’écriture algébrique du nombre complexe z).Le nombre x est appelé partie réel (notée Re(z)) du nombre z et le nombre y est appelé partie imaginaire (notée Im(z)) du nombre complexe z.

Exemple :

Le nombre $z=\sqrt{3}+2i$ est un nombre complexe.

$\sqrt{3}$ est sa partie réelle et 2 est sa partie imaginaire.

Propriétés :

z est un nombre réel si et seulement si Im(z)=0.
z est un imaginaire pur si et seulement si Re(z)=0.

II.Conjugué d’un nombre complexe

Définition :

On considère z un nombre complexe dont la forme algébrique est z=x+iy avec x et y deux nombres réels.On appelle conjugué du nombre z, le nombre complexe, noté $\overline{z}$ , tel que $\overline{z}=x-iy$ .

Exemple :

$\overline{1+3i}=1-3i$ et $\overline{2-5i}=2+5i$ .

Propriétés :

On considère deux nombres complexes $z$ et $z'$ .Nous avons les propriétés suivantes :

$\overline{\overline{z}}=z$
$\overline{z+z'}=\overline{z}+\overline{z'}$
$\overline{(\frac{1}{z})}=\frac{1}{\overline{z}}$ avec $z\neq 0$
$z\in \mathbb{R}\Leftrightarrow \overline{z}=z$
$z$ est un imaginaire pur $\Leftrightarrow \overline{z}=-z$
$\overline{zz'}=\overline{z}\overline{z'}$
$\overline{(\frac{z}{z'})}=\frac{\overline{z}}{\overline{z'}}$ avec $z'\neq 0$
$\overline{(z^n)}=(\overline{z}) ^n$ avec $n\in \mathbb{N}$
$\overline{(kz)}=k \overline{z}$ avec $k\in \mathbb{R}$

III.Représentation graphique des nombres complexes

1. Affixe d’un point

Définition :

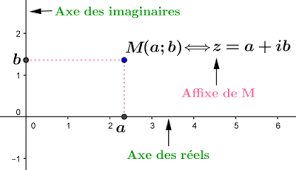
On considère le plan complexe muni d’un repère orthonormé direct $(O,\vec{u},\vec{v})$

On associe à tout nombre complexe z=x+iy , on associe le point M(x;y).

M est appelé le point image de z et z est appelé l’affixe du point M dans le repère orthonormé direct $(O,\vec{u},\vec{v})$ . On note M(z) qui se lit le point M d’affixe z.

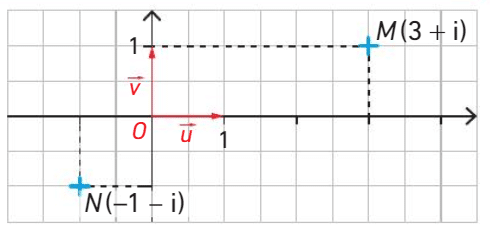
Exemple :

Le point M d’affixe $z=3+i$ a pour coordonnées $M(3,1)$ .

Le point N d’affixe $z=-1-i$ a pour coordonnées $M(-1,-1)$ .

2.Affixe d’un vecteur

Définition :

A tout nombre complexe z affixe du point M(x,y), on associe le vecteur $\vec{w}=\vec{OM}$ tel que $\vec{w}(x;y)$ .et on note $\vec{ w}(z)$ , le vecteur $\vec{ w}$ d’affixe z.

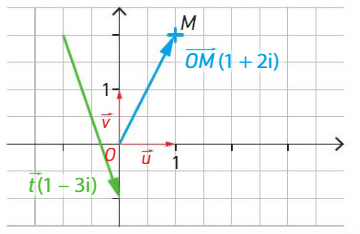
Exemples:

Le vecteur $\vec{OM}$ d’affixe z=1+2i a pour coordonnées $\vec{\,OM}(1;2)$ .

Le vecteur $\vec{t}$ d’affixe 1-3i a pour coordonnées $\vec{\,t}(1;-3)$ .

Propriétés :

On considère deux vecteurs $\vec{w}$ et $\vec{w'}$ d’affixes respectives $z$ et $z'$ .Le vecteur $\vec{w}+\vec{w'}$ a pour affixe $z+z'$ .

Le vecteur $k\vec{w}$ a pour affixe $kz$ avec $k\in \mathbb{R}$ .

3.Les équations du second degré dans 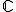$\mathbb{C}$

Propriété :

On considère un nombre réel $a$ .

Si a>0, les solutions sont $z=\sqrt{a}$ et $z=-\sqrt{a}$ ;
Si a<0, les solutions sont $z=i\sqrt{-a}$ et $z=-\sqrt{-a}$ ;
Si a=0, la solution est z=0.

Exemple :

L’équation $z^2=-4$ admet comme solutions dans $\mathbb{C}$ : $z=2i$ et $z=-2i$ .

4.Les équations du type az²+bz+c=0

Propriété :

On considère des nombres réels a,b et c avec $a\neq 0$ .On considère dans $\mathbb{C}$ , l’équation (E) : $az^2+bz+c=0$ de discriminant $\Delta =b^2-4ac$ .

Si $\Delta$ >0, les solutions sont $z_1=\frac{-b+\sqrt{ \Delta }}{2a}$ et $z_2=\frac{-b-\sqrt{ \Delta }}{2a}$ ;
Si $\Delta$ <0, les solutions sont $z_1=\frac{-b+i\sqrt{- \Delta }}{2a}$ et $z_2=\frac{-b-i\sqrt{ -\Delta }}{2a}$ ;
Si $\Delta$ =0, la solution est $z =\frac{ \sqrt{ \Delta }}{2a}$ .