La somme des angles est un calcul fondamental à maîtriser dans ce chapitre sur le triangle.

Exercice 2 : 

Soit ABC un triangle rectangle en A. Montrer que  et  sont complémentaires.
 +  = 180 – 90 = 90° donc ces deux angles sont complémentaires.

Exercice 3 : 

Soit ABC un triangle tel que  et  soient complémentaires. Montrer que ABC est rectangle en A.
donc ABC est rectangle en A.

Exercice 4 : 

Soit ABC un triangle isocèle en A et d la médiatrice de [BC].
1) Montrer que A appartient à d.
ABC est isocèle en A donc AB=AC ainsi A est sur la médiatrice du segment [BC]

2) Déterminer les images de A, B et C par la symétrie d’axe d.
3) Montrer que les angles à la base du triangle ABC sont de même mesure.

Exercice 5 : 

Soit ABC un triangle isocèle en A et ayant un angle de 60°.
1er cas : L’angle de 60° est (BAC) ˆ: Déterminer  et . En déduire que ABC est équilatéral.
Les angles à la base ont la même mesure donc 180-60=120 et 120:2=60 °

2ème cas : L’angle de 60° est  : Déterminer  et . En déduire que ABC est équilatéral.
3ème cas : L’angle de 60° est  : Pourquoi est-il inutile d’étudier ce troisième cas ?

Exercice 6 :  

Soit ABC un triangle quelconque et O le point d’intersection des médiatrices de [AB] et de [AC].
1) Montrer que OA = OB puis que OA = OC.
D’après la propriété de la médiatrice comme O appartient à la médiatrice de [AB] alors OA=OB
et comme O appartient à la médiatrice de [AC] alors OA=OC . 

2) En déduire que O est le centre du cercle circonscrit au triangle.
Nous avons OA=OB et OA=OC donc par transitivité OA=OB=OC donc le cercle de centre O et de rayon OA passe par les trois sommets du triangle ABC, c’est son cercle circonscrit.

3) En déduire également que O appartient aussi à la médiatrice de [BC]
Comme OB=OC alors O appartient à la médiatrice du segment [BC].

Exercice 7 :

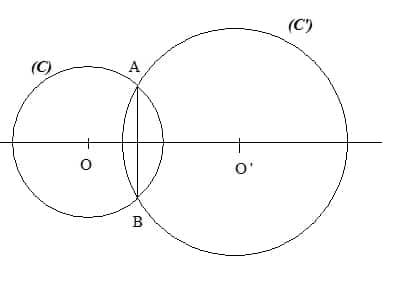
( C ) est un cercle de centre  O  et  de rayon  2 cm.

( C’ )  est un cercle de centre O’ et de rayon  3 cm.

Les deux cercles se coupent en A et B.

Démontre que (OO’)  est la médiatrice de [AB].

Nous avons OA=OB car ce sont des rayons du cercle (C)donc O appartient à la médiatrice du segment [AB] et nous avons O’A=O’B car ce sont des rayons du cercle (C’) donc O’ appartient à la médiatrice du segment [AB].

Donc les points O et O’ appartiennent à la médiatrice du segment [AB], par unicité de la médiatrice d’un segment, on en déduit que (OO’) est la médiatrice du segment [AB].

Exercice 8 :

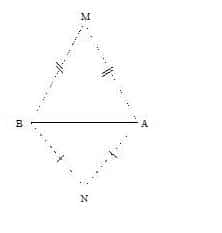
Expliquer pourquoi sur la figure ci-dessous (MN) perpendiculaire à (AB).

M est sur la médiatrice de [AB] et N aussi car MB=MA et NB=NA.

Donc la droite (MN) est la médatrice du segment [AB] ainsi par définition 

de la médiatrice d’un segment, on en déduit que  (MN) perpendiculaire à (AB).

Exercice 9 :

Tracer un segment [AB].

Construire son milieu I sans utiliser de quadrillage ni d’instrument graduée.

Il suffit de tracer la médiatrice du segment [AB] à la règle non graduée et avec le compas.

Exercice 10 :

On donne une droite (d) et un point N qui n’est pas sur cette droite.

Construire deux points A et B de (d) tel que la médiatrice de [AB] passe par N.

Il faut construire le symétrique N’ par rapport à l’axe (d) et construire le losange NAN’B avec A et B sur D.

Exercice 11 :

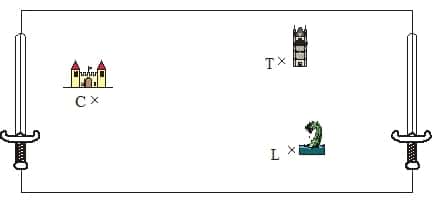
Le bon roi Gatovert a caché son épée magique.

Tu dois la retrouver sur le plan ci-dessous, sachant qu’il l’a enterrée à égale distance de son château C, de la vielle tour T et du lac au dragon L.

Il faut tracer le triangle TLC et deux médiatrices de ce triangle.

Son épée est au point d’intersection de ces deux médiatrices.

Exercice 12 :

a) Tracer trois points R, S et T non alignés.

Construire un point K à égale distance des trois points.

C’est le point d’intersection des médiatrices du triangle RST.

b) Comment s’appelle le point que tu as construit ? Y a-t-il plusieurs solutions ?

C’est le point d’intersection des médiatrices du triangle RST. Non, la solution est unique.

Exercice 13 :

a) Tracer un segment [AB] de longueur 3,8 cm.

Construire un triangle ABC sachant que côté [AC] mesure 5 cm et que le rayon du cercle circonscrit est de 3 cm.

b) Combien y a-t-il de triangles possibles ?

c) Construis-les tous.

Exercice 14 :

a) Construire les triangles EFG et MNP tels que :

· EF 8,4 cm, FG = 7,4 cm et EG = 6,3 cm ;

· MN 5,9 cm, NP = 6,5 cm et MP = 8 cm.

b) Tracer leur cercle circonscrit.

c) Quelle différence y-a-t-il entre les centres de ces deux cercles ?

Exercice 15 :

Construire à chaque fois le cercle circonscrit d’un triangle ABC :

a) AB 4,5 cm, BC 7 cm et  75°.

b) ABC est isocèle en A avec AB = 5 cm et  120°.

c) ABC est équilatéral ce côté 6 cm.

d) ABC est rectangle en A, avec AB = 5 cm et AC = 7 cm.