Corrigé des exercices sur les nombres relatifs en 4ème.

Exercices 6ème

Exercices 5ème

Exercices 4ème

Exercices 3ème

Exercices 1ère

Cours Terminale

Exercices Terminale

Les nombres relatifs en 4ème sont nécessaires à la progression de l’élève tout au long de son année scolaire. Préparez -vous pour les prochains cours à l’avance. Pendant les vacances, procurez-vous le manuel de maths de l’année ou du semestre suivant aussi tôt que possible. Si possible, vous pouvez demander à votre professeur dans quel ordre vous devez aborder les leçons. Quoi qu’il en soit, commencez à étudier aussi tôt que possible et ainsi, lorsque les cours reprendront vous aurez déjà les notions solides.

Participer en classe est parmi les méthodes les plus efficaces pour la compréhension d’un cours. Ainsi, asseyez-vous dans les premiers rangs pour prendre des notes efficaces. Répondez aux questions posées au quart de tour et si vous avez des questions à posez, n’hésitez pas. Vous allez vous surprendre même peut-être à obtenir la meilleure note de la classe. Restez concentré au maximum pour développer des compétences à la fin de ce chapitre sur les nombres relatifs en 4ème.

Exercice 1 :

Calculer les expressions suivantes :

$A = 9 + (-16) + (-8) +22= 7$
$B = - 48 + 24 + 36 + (- 12)=0$
$C = - 7,5 + 12,3 + (- 2,5) + (- 5) + 12,7=10$
$D = - 35 - (- 8) + 14 - 26= - 39$
$E = 54 - 17 - (- 11,5) - 6 + 4 = 46,5$
$F = - 18 + (- 17) - (- 16) + 15 - (- 14) = 10$

Exercice 2 :

Sans effectuer les produits, indiquer les produits égaux.

Si il y a un nombre pair de signes – alors le signe du produit est +.

Si il y a un nombre impair de signes – alors le signe du produit est -.

$A = 2 \times 3 \times 4 \times 5$

$B = - 2 \times (- 3) \times (- 4) \times (- 5 ) = 2 \times 3 \times 4 \times 5 = A$

$C = - 2 \times 3 \times (- 4) \times 5 = 2 \times 3 \times 4 \times 5=A$

$D = - 2 \times (- 3) \times 4 \times (- 5) = - 2 \times 3\times 4 \times 5 = - A$

$E = 2 \times (- 3 )\times (- 4 )\times (- 5) = - 2 \times 3 \times 4 \times 5 = - A$

Exercice 3 :

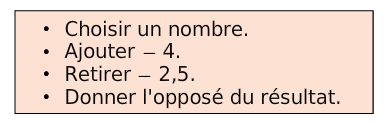
Voici un programme de calcul.

Appliquer ce programme à chacun des nombres suivants :

a. $-(- 2,5 -4-(-2,5))=-(-2,5-4+2,5)=-(-4)=4$

b. $- (0 -4-(-2,5)) =-(0-4+2,5)=-(-1,5)=1,5$

c. $-(1,5-4-(-2,5))=-(1,5-4+2,5)=-(4-4)=0$

d. $-(- 1-4-(-2,5))=-(-5+2,5)=-(-2,5)=2,5.$

Exercice 4 :

Calculer les expressions suivantes :

$A=(-3)\times [3-(+5)]=(-3)\times (-2)=6$

$B=4-[5\times (-2)+(-2)]=4-[-10-2 ]=4-(-12)=4+12=16$

$C=-4\times [(3+(-4))\times (-2-(-3))]=-4\times [(-1)\times (-2+3)]=-4\times [(-1)\times (+1)]=-4\times (-1)=4$

Exercice 5 :

Calculer les expressions suivantes :

$A=\frac{11\times (-3)}{(-5)\times (-2)}=\frac{-33}{10}=-3,3$

$B=\frac{(-3)\times 2\times (-5)}{-10\times 4}=\frac{30}{-40}=-\frac{3}{4}=-0,75$

$C=-\frac{7\times (-2)\times 8}{14\times 5}=-\frac{-112}{70}=\frac{112}{70}=1,6$

$D=\frac{(-1)\times (-3)\times (-2)\times (-1)}{5\times (-4)}=\frac{6}{-20}=-\frac{6:2}{20:2}=-\frac{3}{10}=-0,3$