Les calculs d’aires sont à maîtriser impérativement par les élèves en 5ème. En effet, ce chapitre leur procure de nouvelles compétences en maths. En outre, avec les calculs d’aires et de périmètres en 5ème, vous allez progresser tout au long de l’année scolaire.
Exercice 1 : Pour prendre un bon départ sur les formules d’aires.
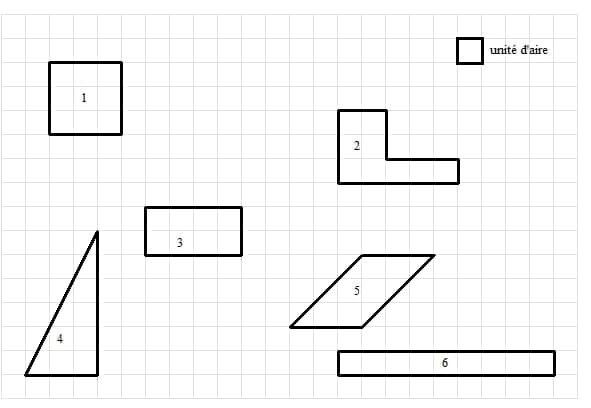
A – « L’intrus » : Sur le quadrillage ci-dessous, on a dessiné six figures.
Sachant que l’unité d’aire est le carreau, calcule l’aire de chacune des 6 figures et trouve ainsi l’intrus .
Aire de la figure 1 : 9 u.a ; Aire de la figure 2 : 9 u.a ; Aire de la figure 3 : 8 u.a ;
Aire de la figure 4 :9 u.a ; Aire de la figure 5 : 9 u.a ; Aire de la figure 6 : 9 u.a ;
L’intrus est la figure 3.
B – 1°) Complète:
Aire du rectangle : Aire = Lxl avec L : la longueur l : la largeur
Aire du carré : Aire = cxc = c2 avec c : le côté
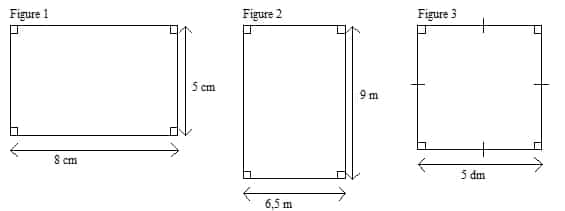
2°) Calcule l’aire des figures suivantes:
Figure 1 : Aire = 5×8=40 cm².
Figure 2 : Aire =6,5×9=58,5 cm².
Figure 3 : Aire = 5×5=25 dm².
Exercice 2 : Revoir les UNITES D’AIRE.
|
km² |
hm² |
dam² |
m² |
dm² |
cm² |
mm² |
|||||||
|
|
ha |
a |
ca |
|
|
|
|||||||
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
1 m² = 100 dm² = 10 000cm² = 1 000 000 mm²
1 m² = 0,01 dam² = 0,000 1 hm² = 0,000 001 km²
ca = 1 m² 1 a = 1 dam² 1 ha = 1 hm²
- Indique une unité appropriée pour exprimer chaque longueur ou chaque aire :
a) la hauteur de la salle de classe : 3 m b) l’étendue d’un champ :300 m
c) la distance Paris – Lyon : 400 km d) la superficie d’une table : 6 m²
e) le périmètre d’un stade : 600 m f) l’aire d’un confetti : 6 mm²
- Complète :
360 cm² = 3,6 dm² 1 km² = 1 000 000 m² 10 000 m² = 1 hm².
8 m² = 800 dm ² = 80 000 cm² .
145 cm² = 0,014 5 m² = 1 450 000 mm²
0,1 dam ² =10 m² = 0,000 01km²
- Complète :
| 15,4 m ² =1 540dm ²
|
154 km ² =15 400 000 000 dm ² |
| 0,02 cm ² = 200 mm ²
|
2 024 mm ² = 0,02024 m ² |
| 3,5 dam ² = 3 500 000 cm ²
|
6 325 cm ² = 0,6325 m ² |
| 4,9 km ² = 4 900 000 m ²
|
3 060 mm ² = 0,306 cm ² |
| 2,74 dm ² =274 cm ²
|
58 830 cm ² = 5,883 m ² |
| 0,68 cm ² =68 mm ²
|
46 000 m ² =0,046 km ² |
| 1 600 m ² =0,001 6 km ²
|
172 mm ² = 1,7 2 cm ² |
| 3 m ² =30 000 cm ²
|
7,2 mm ² =0,072 cm ² |
| 3 ha =300a=3×100=300 m ²
|
18 ha = 18×100 a=800 a=800×100 m²=80 000 m² =800 000 000 cm² |
Exercice 3 :
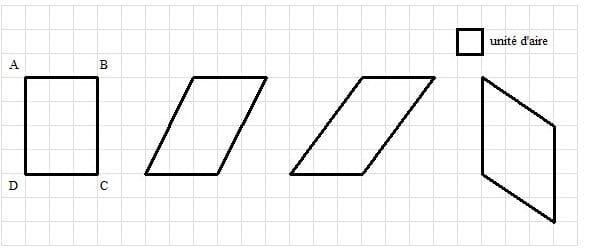
En prenant comme unité d’aire le carreau, donne l’aire du rectangle ABCD puis l’aire de chacun des parallélogrammes.
3×4=12 3×4=12 3×4=12 4×3 = 12
Exercice 4 :
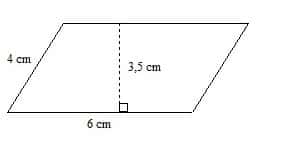
La figure ci-dessous est un parallélogramme.
1° Calculer son aire.
6×3,5=21 cm²
2° Calculer son périmètre.
2x(4+6)=20 cm
Exercice 5 :
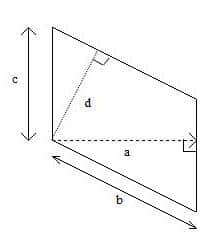
On considère le parallélogramme ci-dessous.
( a et d désignent les hauteurs ) .
Entourer les produits qui expriment l’aire de ce parallélogramme ?
|
a |
c |
b |
a |
a |
b |
Exercice 6 :
Compléter le tableau suivant, où c désigne un côté de parallélogramme, h la hauteur relative à ce côté, et A l’aire du parallélogramme:
|
c |
h |
A |
|
7,3 cm |
5,4 cm |
39,42 cm² |
|
225 m |
2 dam |
4,5 dam2 |
|
5 m |
2,3 m |
11,5 m2 |
|
… m |
15 cm |
4,5 m2 |