Corrigé des exercices sur les suites numériques en terminale.

EXERCICE N°1 :

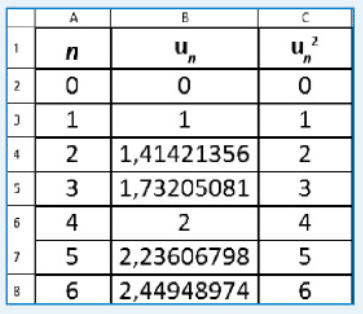
En observant les premières valeurs de $u_n$ et $u_n^2$ , on peut conjecturer que $u_n=\sqrt{4^n-1}$ pour tout $n\in\mathbb{N}$ .

On peut le démontrer par récurrence.
Initialisation :

Pour n=0, on a $u_0=0=\sqrt{4^0-1}$ . L’hypothèse est vérifiée au rang 0.
Hérédité :

Supposons que $u_n=\sqrt{4^n-1}$ vraie pour un certain entier n.

Alors,
$u_{n+1}=\sqrt{u_n^2+1}=\sqrt{(4^n-1)+1}=\sqrt{4^{n+1}-1}$ .
Ainsi, l’hypothèse est vérifiée au rang $n+1$ .
Conclusion :

On en déduit que $u_n=\sqrt{4^n-1}$ pour tout $n\in\mathbb{N}$ .

EXERCICE N°2 :

Initialisation :

Pour n=0, on a $V_0=0=0(0+1)$ . L’hypothèse est vérifiée au rang 0.

Hérédité :

Supposons que $V_n=n(n+1)$ soit vraie pour un certain entier n.

Alors,
$V_{n+1}=V_n+2n+2=(n+1)(n+2)= (n+1)((n+1)+1)$ .
Ainsi, l’hypothèse est vérifiée au rang $n+1$ .

Conclusion :

On en déduit que pour tout $n\in\mathbb{N}, V_n=n(n+1)$ .

EXERCICE N°3 :

Initialisation :

Pour n=0, on a $2^0=1\geq 1+1$ .

L’hypothèse est vérifiée au rang 0.
Hérédité :

Supposons $2^n\geq n+1$ pour un certain entier n.

On a alors :
$2^{n+1}=2\times 2^n\geq 2(n+1)\geq n+2+1$ .
Ainsi, l’hypothèse est vérifiée au rang $n+1$ .
Conclusion :

On en déduit que $2^n\geq n+1$ pour tout entier naturel n.

EXERCICE N°4 :

Initialisation :

Pour n=0, on a $OA_0=1=\sqrt{4\times 0+1}$ .

L’hypothèse est vérifiée au rang 0.
Hérédité :

Supposons que $OA_n=\sqrt{4n+1}$ pour un certain entier n.

On a alors :
$OA_{n+1}=\sqrt{OA_n^2+A_nA_{n+1}^2}=\sqrt{(4n+1)+4}=\sqrt{4(n+1)+1}$ .
Ainsi, l’hypothèse est vérifiée au rang $n+1$ .
Conclusion :

On en déduit que $OA_n=\sqrt{4n+1}$ pour tout $n\in\mathbb{N}$ .

EXERCICE N°5 :

1) a) On a $\lim_{n\to \infty}0,9^n=0$ et donc $\lim _{n\to \infty}u_n=3(2-0)=6$ .
b) On a $\lim _{n\to \infty}1,01^n=+\infty$ et donc $\lim _{n\to \infty}v_n=+\infty$ .
c) On a $\lim _{n\to \infty}0,9^n=0$ et $\lim _{n\to \infty}3+0,2^n=3$ , donc $\lim _{n\to \infty}w_n=\frac{3}{0-5}=-\frac{3}{5}$ .
d) On peut réécrire $t_n$ sous la forme \frac{4^n}{3^n}+\frac{5}{3^n}. On a $\lim _{n\to \infty}\frac{4^n}{3^n}=+\infty$ et $\lim _{n\to \infty}\frac{5}{3^n}=0$ , donc $\lim _{n\to \infty}t_n=+\infty$ .

2) a) Le premier terme de la suite est -3.

On peut écrire $S_n=\frac{-3(1-0,8^n)}{1-0,8}$ .

En effet,

$S_n=u_1(1+0,8+0,8^2+...+0,8^{n-1})=-3(1+0,8+0,8^2+...+0,8^{n-1})=-3\frac{1-0,8^n}{1-0,8}$ .
b) La suite $(S_n)$ est convergente car $|0,8|<1$ , et sa limite est $\frac{-3}{1-0,8}=15$ .

EXERCICE N°6 :

On a $u_n=(-3)\times 0,8^{n-1}$ .

Ainsi, $S_n=-3\frac{1-0,8^n}{1-0,8}=3(0,8^n-1)$ .

On en déduit que la limite de la suite $(S_n)$ est $3\times (-1)=-3$ .

EXERCICE N°7 :

1) a) La fonction f est dérivable sur $]0;+\infty[$ et on a $f'(x)=\frac{3}{(1+2x)^2}>0$ pour tout $x>0$ .

Donc, f est strictement croissante sur $[0;+\infty[$ .
b) Si $x\in[0;1]$ , alors $f'(x)=\frac{3}{(1+2x)^2}\leq \frac{3}{(1+2\times 1)^2}=1$ .

2) Initialisation :

Pour n=0, on a $u_0=0,7\geq 0 et u_0\leq 1$ .

L’hypothèse est vérifiée au rang 0.

Hérédité :

Supposons que $0\leq u_n\leq 1$ pour un certain entier n soit vraie.

Alors, $0\leq 3u_n\leq 3$ et $0\leq 2u_n<2$ , donc
$0\leq u_{n+1}=\frac{3u_n}{1+2u_n}<\frac{3}{1}=3$

et
$0\leq u_{n+1}=\frac{3u_n}{1+2u_n}\geq 0$ .
Ainsi, l’hypothèse est vérifiée au rang $n+1$ .

Conclusion :

On en déduit que pour tout $n\in\mathbb{N}, 0\leq u_n\leq 1$ .

3) La suite $(u_n)$ est décroissante et minorée par 0, donc elle converge.

Soit l sa limite.

En passant à la limite dans la relation de récurrence, on a $l=\frac{3l}{1+2l}$ .

Cette équation admet $l=0$ comme solution, qui est la seule solution possible car f est strictement croissante sur [0;1].

Ainsi, la suite $(u_n)$ converge vers 0.

EXERCICE N°8 :

1) Les dix premiers termes de la suite $(u_n)$ sont :
1, 4, 9, 16, 25, 36, 49, 64, 81, 100.

2) a) On peut conjecturer que u_n=n^2.

b) Initialisation :

Pour n=1, on a $u_1=1=1(1+1)$ . L’hypothèse est vérifiée au rang 1.
Hérédité :

Supposons que $u_n=n^2$ pour un certain entier n.

Alors,
$u_{n+1}=u_n+2n+1=n^2+2n+1=(n+1)^2$ .
Ainsi, l’hypothèse est vérifiée au rang n+1.
Conclusion :

On en déduit que pour tout $n\in\mathbb{N}, u_n=n^2$ .

EXERCICE N°9 :

Initialisation :

Pour n=1, on a $1^2=\frac{1\times 2\times 3}{6}$ .

L’hypothèse est vérifiée au rang 1.
Hérédité :

Supposons $\sum\limits_{q=1}^{n}q^2=\frac{n(n+1)(2n+1)}{6}$ .

Alors,
$\sum\limits_{q=1}^{n+1}q^2 \\\\=\sum\limits_{q=1}^{n}q^2+(n+1)^2=\frac{n(n+1)(2n+1)}{6}+(n+1)^2 \\\\(n+1)\,\frac{2n^2+7n+6}{6} \\\\(n+1)\,\frac{(n+1)(2n+3)}{6} \\\\=\frac{(n+1)(n+2)(2n+3)}{6}$ .

Ainsi, l’hypothèse est vérifiée au rang n+1.
Conclusion :

On en déduit que pour tout entier naturel n non nul,

$\sum_{q=1}^{n}q^2=\frac{n(n+1)(2n+1)}{6}$ .

EXERCICE N°10 :

1) a) On a $\lim\limits_{n\to \infty}u_n=\lim\limits_{n\to \infty}\frac{4^n+5}{2\times 3^n}=0$ car $\frac{4^n+5}{2\times 3^n}\leq \frac{4^n+5^n}{2\times 3^n}= (\frac{4}{5})^n+\frac{5}{2}\times (\frac{2}{3})^n$ qui tend vers 0 quand n tend vers l’infini.

b) On a $\lim\limits_{n\to \infty}v_n=\lim\limits_{n\to \infty}(1+\frac{2n-5}{3+2n})=1$ .
c) On a $l=\lim\limits_{n\to \infty}\frac{4n-1+\frac{5}{\sqrt{n}}}{n}=4+\lim\limits_{n\to \infty}\frac{5}{n^{\frac{3}{2}}}=4$ .

d) On a $\lim\limits_{n\to \infty}t_n=+\infty$ .

2) a) La suite $(u_n)$ est géométrique de raison 0,8 et de premier terme -3.

Ainsi, $u_n=(-3)\times 0,8^{n-1}$ .

b) On a $\lim\limits_{n\to \infty}u_n=\lim\limits_{n\to \infty}(-3)\times 0,8^{n-1}=0$ .

3) Les trois dernières suites tendent toutes vers 0, donc elles sont bornées.

EXERCICE N°11 :

1) On a $v_n=4u_n-3=4(-\frac{1}{3}u_{n-1}+1)-3=-\frac{4}{3}v_{n-1}$ .
Ainsi, la suite $(v_n)$ est géométrique de raison $-\frac{1}{3}$ , et son premier terme est $v_0=4u_0-3=1$ .

2) On peut écrire $v_n=4u_n-3=4(-\frac{1}{3})^n+4-3=-\frac{17}{4}\times (\frac{-1}{3})^n+\frac{1}{4}$ .
Ainsi, $u_n=\frac{17}{4}\times (\frac{-1}{3})^n+\frac{3}{4}$ .