Corrigé des exercices sur les intégrales en terminale.

EXERCICE N°1 :

a) L’intégrale de $3dx$ entre 0 et 4 vaut :

$\int_{0}^{4}3dx=3\times(4-0)=12$

b) L’intégrale de $(\frac{1}{2}t+2)dt$ entre 3 et 7 vaut :

$\int_{3}^{7}(\frac{1}{2}t+2)dt=[\frac{1}{4}t^2+2t]_{3}^{7}=(\frac{1}{4}(7)^2+2(7))-(\frac{1}{4}(3)^2+2(3))=15$

EXERCICE N°2 :

Pour déterminer si les fonctions proposées sont des primitives de f, il suffit de dériver chaque fonction et de voir si on obtient f.

a) On a : $F'_1(x)=\frac{e^x}{\,(e^x+1\,\,)^2}\times\frac{-1}{e^x+1}=-\frac{e^x}{\,(e^x+1\,\,)^3}$

$F'_1(x)$ est différente de f(x), donc $F_1(x)$ n’est pas une primitive de f(x).

b) On a : $F'_2(x)=\frac{e^x}{\,(e^x+1\,\,)^2}\times\frac{2e^x+1}{e^x+1}-\frac{e^x}{\,(e^x+1\,\,)^2}\times\frac{(2e^x+1)^2}{\,(e^x+1\,\,)^2}=\frac{e^x}{\,(e^x+1\,\,)^3}(e^x-1)$

$F'_2(x)$ est égale à f(x), donc $F_2(x)$ est une primitive de f(x).

c) On a : $F'_3(x)=\frac{-2e^{-2x}}{\,(e^{-x}+1\,\,)^2}-\frac{(2e^{-x}+1)(-e^{-x})}{\,(e^{-x}+1\,\,)^2}=-\frac{e^{-x}}{\,(e^{-x}+1\,\,)^2}$

$F'_3(x)$ est différente de f(x), donc $F_3(x)$ n’est pas une primitive de f(x).

d) On a : $F'_4(x)=\frac{-e^{-x}(e^{-x}+2)}{\,(e^{-x}+1\,\,)^2}+\frac{(e^{-x}+2)(-e^{-x})}{\,(e^{-x}+1\,\,)^2}=-\frac{e^{-x}}{\,(e^{-x}+1\,\,)^2}$

$F'_4(x)$ est égale à f(x), donc $F_4(x)$ est une primitive de f(x).

EXERCICE N°3 :

a) Une primitive de $5x^4-3x+7$ est : $\frac{5}{5}x^5-\frac{3}{2}x^2+7x+C$ , où C est une constante d’intégration.

b) Une primitive de $4(3x-1)^5$ est : $\frac{4}{18}(3x-1)^6+C$ , où C est une constante d’intégration.

c) Pour trouver une primitive de $\frac{7x}{x^2+4}$ , on fait le changement de variable $u=x^2+4$ .

Alors, on a :

$\int\frac{7x}{x^2+4}dx=\frac{1}{2}\int\frac{7}{u}du=7ln|u|+C=7ln|x^2+4|+C$

d) Une primitive de 3xe^x est : $(3x-3)e^x+C$ , où C est une constante d’intégration.

EXERCICE N°4 :

a) On a 2-2e^t\leq 0 pour tout t réel, car $e^t\geq 1$ pour $t\geq 0$ et donc $e^t-1\geq 0$ .

De plus, $2-2e^t=(1-e^t)(1+e^t)\leq 0$ car $1-e^t\leq 0$ et $1+e^t\geq 0$ pour tout t réel.

b) On a $e^{t^2}\geq e^t$ pour tout $t\geq 1$ , car $t^2>t$ pour tout t>1 et donc $e^{t^2}>e^t$ . Donc :

$2-2e^{t^2}\leq 2-2e^t$

c) On a :

$\int_{0}^{1}(2-2e^{t^2})dt\leq\int_{0}^{1}(2-2e^t)dt$

$\Rightarrow\,\,\,\int_{0}^{1}(2-2e^{t^2})dt\leq 2-2(e-1)$

Mais on a aussi :

$2-2(e-1)\leq\int_{0}^{1}(2-2e^{t^2})dt$

$\Rightarrow\,\,\,0\leq\int_{0}^{1}(2-2e^{t^2})dt\leq ln2$

Donc, on a :

$0\leq\int_{0}^{1}\frac{x^n}{1+x}dx\leq ln2$

EXERCICE N°5 :

a) On utilise une intégration par parties pour calculer :

$\int_{0}^{1}\frac{x^n}{1+x}dx=[ln(1+x)\times\frac{x^n}{n+1}]_{0}^{1}-\int_{0}^{1}\frac{1}{(1+x)^2}\times\frac{x^n}{n+1}dx$

$=ln2\times\frac{1}{n+1}-\frac{1}{n+1}\int_{0}^{1}\frac{1}{(1+x)^2}\times d(x^{n+1})$

$=ln2\times\frac{1}{n+1}-\frac{1}{n+1}[x^{n+1}\times\frac{-1}{1+x}]_{0}^{1}+\frac{1}{n+1}\int_{0}^{1}\frac{x^{n+2}}{(1+x)^2}dx$

$=ln2\times\frac{1}{n+1}+\frac{1}{n+1}\int_{0}^{1}\frac{x^{n+2}-x^{n+1}}{(1+x)^2}dx$

$=ln2\times\frac{1}{n+1}+\frac{1}{n+1}\int_{0}^{1}(\frac{x^{n+2}}{(1+x)^2}-\frac{x^{n+1}}{(1+x)^2})dx$

$=ln2\times\frac{1}{n+1}+\frac{1}{n+1}\int_{0}^{1}(\frac{x^{n+2}}{1+x}-\frac{x^{n+1}}{1+x})\times\frac{1}{1+x}dx$

$\Rightarrow\,\,\,0\leq\int_{0}^{1}\frac{x^n}{1+x}dx\leq ln2$

EXERCICE N°6 :

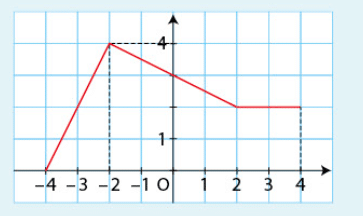
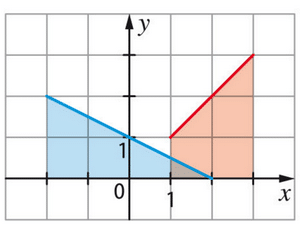
a) Pour calculer $\int_{-4}^{-2}f(t)dt$ , on utilise l’aire sous la courbe entre -4 et -2.

Cette aire est représentée par un rectangle de base 2 et de hauteur 0,5.

Donc :

$\int_{-4}^{-2}f(t)dt=Aire=2\times0,5=1$

b) Pour calculer $\int_{-2}^{2}f(t)dt$ , on utilise l’aire sous la courbe entre -2 et 2.

Cette aire est représentée par un rectangle de base 4 et de hauteur 1. Donc :

$\int_{-2}^{2}f(t)dt=Aire=4\times1=4$

c) Pour calculer $\int_{2}^{4}f(t)d$ t, on utilise l’aire sous la courbe entre 2 et 4.

Cette aire est représentée par un rectangle de base 2 et de hauteur -0,5. Donc :

$\int_{2}^{4}f(t)dt=Aire=2\times(-0,5)=-1$

EXERCICE N°7 :

a) $\int_{-2}^{1}5dx=5\times(1-(-2))=15$

b) $\int_{-1}^{2}(-t+4)dt=[-\frac{1}{2}t^2+4t]_{-1}^{2}=(-\frac{1}{2}(2)^2+4(2))-(-\frac{1}{2}(-1)^2+4(-1))=7$

c) $\int_{-3}^{3}(x+3)dx=[\frac{1}{2}x^2+3x]_{-3}^{3}=(\frac{1}{2}(3)^2+3(3))-(\frac{1}{2}(-3)^2+3(-3))=18$

d) $\int_{0}^{5}(2x+1)dx=2\times\frac{5^2}{2}+5=30$

e) $\int_{-2}^{2}(1-\frac{x}{2})dx=[x-\frac{x^2}{4}]_{-2}^{2}=(2-\frac{4}{4})-(-2-\frac{4}{4})=4$

f) $\int_{-1}^{1}(1-|x|)dx=2\int_{0}^{1}(1-x)dx=2[x-\frac{x^2}{2}]_{0}^{1}=2-(0-0)=2$

EXERCICE N°8 :

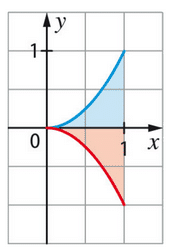
1. L’aire en bleu est délimitée par la courbe de $f(x)=x^2$ entre x=0 et x=1, ainsi que par la droite $y=-x^2$ .

L’intersection entre les deux courbes est lorsque $x=\sqrt{\frac{1}{2}}$ .

L’aire de la surface en bleu est donc la somme de l’intégrale suivante :

$\int_{0}^{\sqrt{\frac{1}{2}}}(x^2-(-x^2))dx=2\int_{0}^{\sqrt{\frac{1}{2}}}x^2dx=\frac{1}{3}$

L’aire en bleu est donc $\frac{1}{3}$ unité d’aire.

2. La surface en rouge est le complémentaire de la surface en bleu par rapport à l’aire délimitée par les courbes de f(x) et g(x).

Comme f(x) est au-dessus de g(x) sur [0;1], la surface en rouge est la somme des aires de f(x) sur $[0;\sqrt{\frac{1}{2}}]$ et de g(x) sur $[\sqrt{\frac{1}{2}};1]$ .

Comme les aires délimitées par f(x) et g(x) sont symétriques par rapport à l’axe des ordonnées, elles ont la même aire.

Donc, l’aire de la surface en rouge est la moitié de l’aire de l’aire délimitée par f(x) sur [0;1], qui est :

$\int_{0}^{1}f(x)dx=\int_{0}^{1}x^2dx=\frac{1}{3}$

L’aire en rouge est donc $\frac{1}{6}$ unité d’aire.

3. La surface en bleu est délimitée par la courbe de $f(x)=x^2$ entre x=0 et x=1, ainsi que par la droite $y=-x^2$ .

Donc, l’aire de la surface en bleu est :

$\int_{0}^{1}(x^2-(-x^2))dx=2\int_{0}^{1}x^2dx=\frac{2}{3}$

On retrouve bien l’aire précédemment calculée.

EXERCICE N°9 :

$I=\int_{1}^{3}xdx=[\frac{1}{2}x^2]_{1}^{3}=\frac{1}{2}(3)^2-\frac{1}{2}(1)^2=\frac{8}{2}=4$

$J=\int_{-2}^{2}-0,5x+1dx=[-\frac{1}{4}x^2+x]_{-2}^{2}=(-\frac{1}{4}(2)^2+2)-(-\frac{1}{4}(-2)^2-2)=-1$

Donc $I \neq J$ . L’affirmation est fausse.

EXERCICE N°10 :

1) Une primitive de $2xe^{x^2-3}$ est $e^{x^2-3}+C$ , où C est une constante d’intégration.

Une primitive de $\frac{x}{x^2+4}$ est $\frac{1}{2}ln(x^2+4)+C$ , où C est une constante d’intégration.

Pour trouver une primitive de $cos(x)sin^2(x)$ , on fait le changement de variable $u=sin(x)$ .

Alors, on a :

$\int cos(x)sin^2(x)dx=-\int u^2du=-\frac{u^3}{3}=-\frac{sin^3(x)}{3}+C$

2) Une primitive de $\frac{2x+1}{x^2+x+1}$ est $ln(x^2+x+1)+C$ , où C est une constante d’intégration.

Une primitive de $\frac{x}{(x^2+1)^2}$ est $-\frac{1}{2}\frac{x}{x^2+1}-\frac{1}{2}arctan(x)+C$ , où C est une constante d’intégration.

Pour trouver une primitive de $x(x^2+5)^{-3}$ , on utilise la substitution $u=x^2+5$ . Alors, on a :

$\int x(x^2+5)^{-3}dx=\frac{1}{2}\int u^{-3/2}du=-u^{-1/2}=-\frac{1}{\sqrt{x^2+5}}+C$

3) Une primitive de $xe^{-x^2}$ est $-\frac{1}{2}e^{-x^2}+C$ , où C est une constante d’intégration.

Une primitive de $\frac{e^x}{e^x+1}$ est $ln(e^x+1)-x+C$ , où C est une constante d’intégration.

Pour trouver une primitive de $\frac{8x}{\sqrt{2x^2+1}}$ , on fait le changement de variable $u=2x^2+1$ .

Alors, on a :

$\int \frac{8x}{\sqrt{2x^2+1}}dx=\int u^{-1/2}du=2\sqrt{2x^2+1}+C$

EXERCICE N°11 :

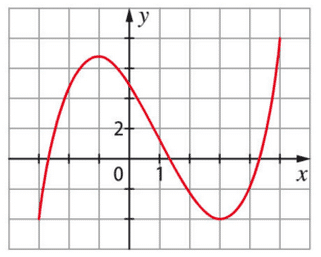
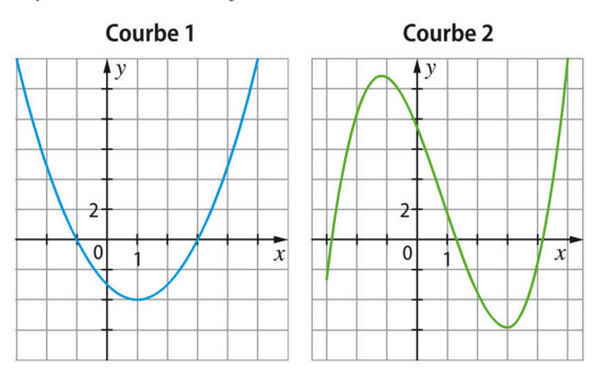
La fonction f est la dérivée de F.

On sait que F est croissante sur [0;2] et décroissante sur [2;5], donc f est positive sur [0;2] et négative sur [2;5].

La première courbe est donc celle de $f(x)$ tandis que la deuxième est celle de $-f(x)$ .

EXERCICE N°12 :

1.a) Pour tout $x\in [n;n+1]$ , on a $n\leq x\leq n+1$ , donc $\frac{1}{n+1}\leq\frac{1}{x}\leq\frac{1}{n}$ .

b) Une primitive de $\frac{1}{n}$ est $ln|x|$ , donc :

$\int_{n}^{n+1}\frac{1}{n}dx=ln|n+1|-ln|n|=ln(\frac{n+1}{n})$

c) En utilisant les inégalités de la question a), on a :

$\int_{n}^{n+1}\frac{1}{n+1}dx\leq\int_{n}^{n+1}\frac{1}{x}dx\leq\int_{n}^{n+1}\frac{1}{n}dx \Rightarrow\,\,\,I_{n}\leq\frac{1}{n+1}\leq I_{n}$

Donc, on a : $\frac{1}{n+1}\leq I_{n}\leq\frac{1}{n}$

2) La limite quand n tend vers l’infini de $\frac{1}{n+1}$ est 0 et la limite quand n tend vers l’infini de $\frac{1}{n}$ est aussi 0.

Donc, par le théorème des gendarmes, la limite de la suite $(I_n)$ est 0 également.

Corrigé des exercices sur les intégrales en terminale.

Corrigé des exercices sur les intégrales en terminale.

Corrigé des exercices sur les probabilités en terminale.

Corrigé des exercices sur le produit scalaire en terminale.

Corrigé des exercices sur les limites de fonctions en terminale.

Notez Mathématiques Web !