Le parallélogramme à travers un cours de maths en 5ème à suivre intégralement pour progresser tout au long de l’année.
Cette leçon fait intervenir les notions suivantes :
- définition;
- propriété des cotés opposés;
- propriété des angles opposés;
- propriété des diagonales;
- le rectangle, le losange, le rectangle et le carré.
L’élève devra être capable de tracer à l’aide du matériel de géométrie ( règle, équerre, compas et rapporteur) mais également, savoir utiliser les différentes propriétés de cette figure concernant ses côtés opposés, ses angles opposés et ses diagonales. Nous terminerons ce chapitre par l’étude des parallélogrammes particuliers comme le rectangle le losange et le carré en classe de cinquième.
I. Le parallélogramme
1.Définition
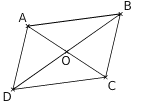
C’ est un quadrilatère ayant ses côtés opposées parallèles deux à deux.
Exemple :
Les droites (AB) et (DC) sont parallèles.
Les droites (AD) et (BC) sont parallèles.
Le quadrilatère ABCD est un parallélogramme.
Le centre de symétrie est le point O qui correspond au point d’intersection de ses diagonales.
Remarque :
Le point O est le centre de symétrie du parallélogramme ABCD.
L’image du segment [AB] par la symétrie de centre O est le segment [DC].
L’image de l’angle par la symétrie de centre O est l’angle
.
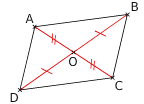
Les diagonales de cette figure se coupent en leur milieu.
Preuve :
Si un quadrilatère est un parallélogramme alors son centre de symétrie est le point d’intersection des diagonales.
Par définition du centre de symétrie, on en déduit que O est le milieu de [AC] et O est le milieu de [BD].
Par conséquent, les diagonales [AC] et [BD] se coupent en leur milieu O qui est le centre de symétrie du parallélogramme.
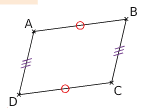
Les côtés opposés d’un parallélogramme ont la même longueur.
Preuve :
Si un quadrilatère est un parallélogramme alors son centre de symétrie est le point d’intersection des diagonales.
Le symétrique du segment [AB] est [DC] et le symétrique du segment [AD] est [BC].
La symétrie centrale conserve les longueurs de segments donc AB=DC et AD=BC.
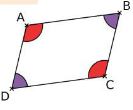
Les angles opposés d’un parallélogramme ont la même mesure.
Preuve :
Si un quadrilatère est un parallélogramme alors son centre de symétrie est le point d’intersection des diagonales.
L’mage de l’angle par la symétrie de centre O est l’angle
.
L’image de l’angle par la symétrie de centre O est l’angle
.
La symétrie centrale conserve les mesures d’angles donc et
.
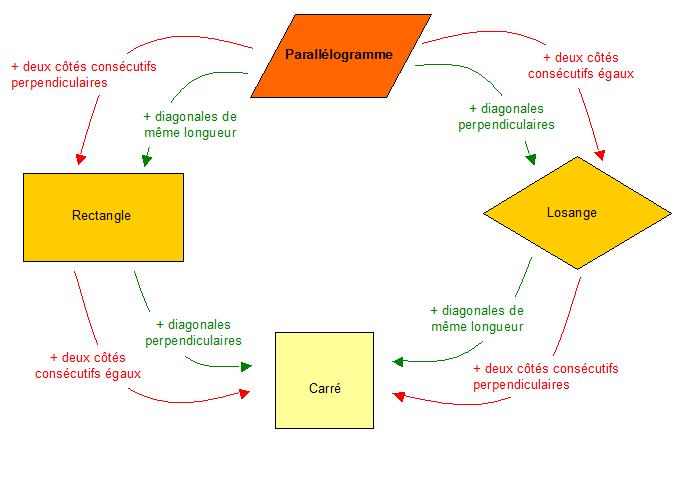
II.Les parallélogrammes particuliers
Un rectangle, un losange et un carré sont des parallélogrammes particuliers.
Un carré est à la fois un losange et un rectangle, il cumule toutes les propriétés du losange et du rectangle.
Application :
Ces affirmations sont-elles vraies ou fausses ?
- Un parallélogramme a deux axes de symétrie.
- Si E et F sont les symétriques respectifs de G et H par rapport à ,alors EFGH est un parallélogramme de centre O.
- Un parallélogramme a quatre angles égaux.
- Si un quadrilatère a trois angles droits, alors c’est un rectangle.
- Si un quadrilatère a trois côtés égaux, alors c’est un losange.