Homothéties : cours de maths en 3ème en PDF.
I. L’homothétie :
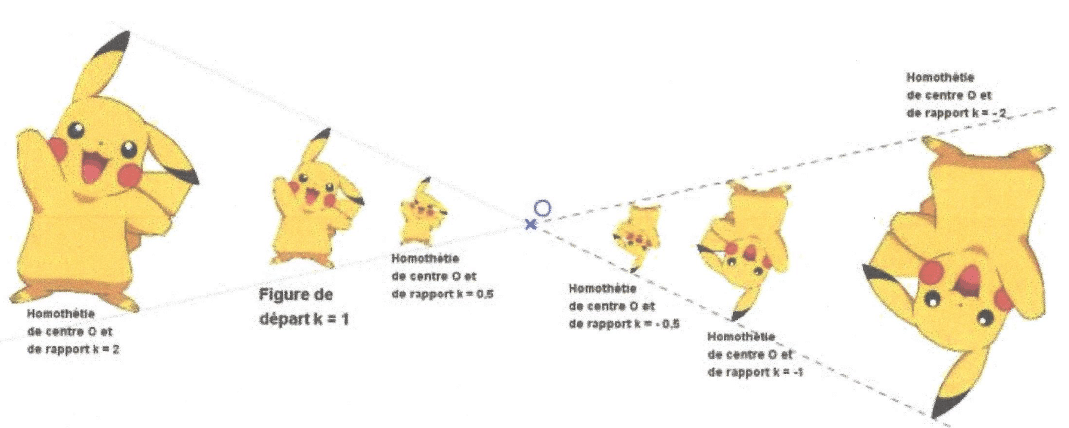
Transformer une figure par une homothétie de centre O, c’est l’agrandir ou la réduireen faisant glisser les points le long des droites passant par O.
L’image d’un point M par l’homothétie de centre O et de rapport k>0 est le point M’ tel que :
- M’ appartient à la demi-droite [OM);
.
Une homothétie conserve :
- l’alignement;
- la mesure des angles
- le parallélisme.
Si k >0, alors l’homothétie multiplie :
- les longueurs par k;
- les aires par
.
L’homothétie transforme une droite en une autre droite qui lui est parallèles.
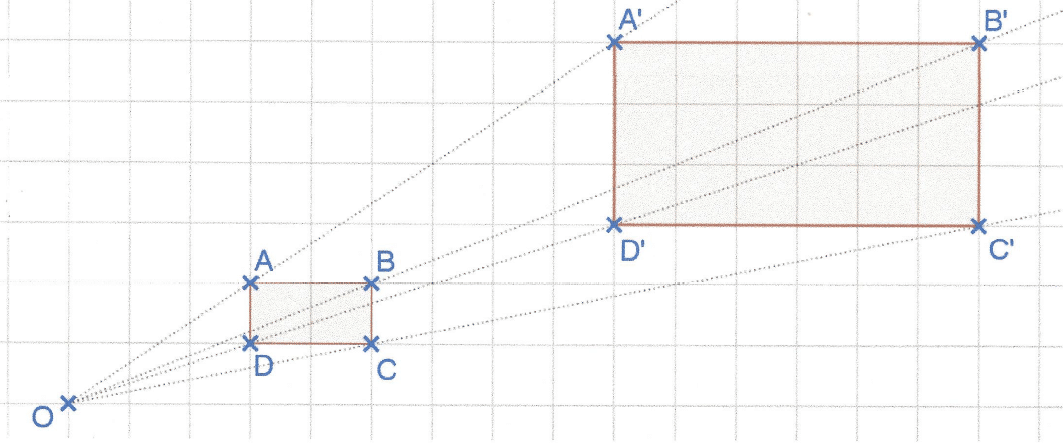
Exemple :
Le rectangle A’B’C’D’ est l’image du rectangle ABCD par l’homothétie de centre O et de rapport k=3.
AB = 2 cm donc .
donc
.
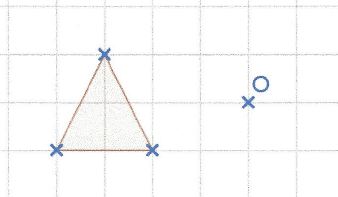
Application 1 :
Construire les images du triangle par les homothéties de centre O et de rapport 3;-1 et – 2.
Remarque :
L’image du triangle de départ par l’homothétie de centre O et de rapport – 1 est en fait une symétrie centrale de centre O.
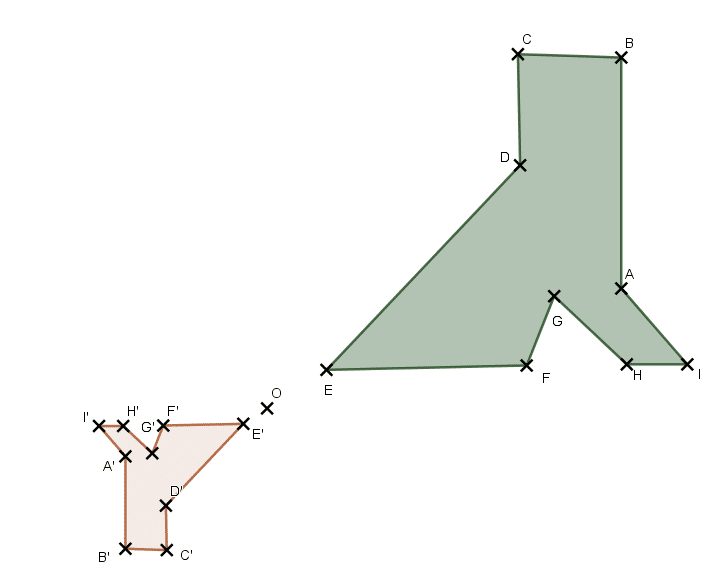
Application 2 :
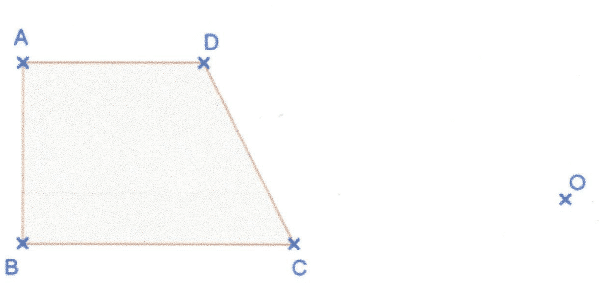
Construire les images du trapèze rectangle ABCD par les homothéties de centre O et de rapport et – 0,8.
Application 3 :
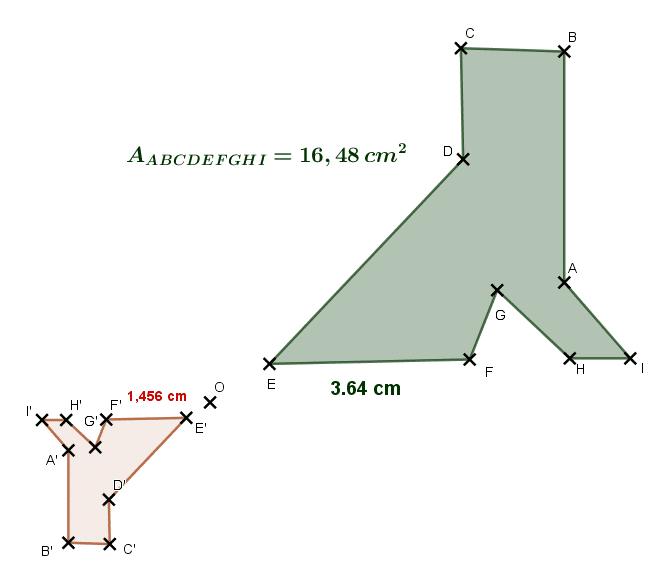
On considère l’homothétie de centre O et de rapport k qui transforme la chaussure verte en la chaussure rouge.
- Est-ce un agrandissement ou une réduction ? justifier votre réponse.
- Quel est la valeur du rapport k?
- Calculer l’aire de la chaussure rouge (arrondir le résultat au centième).
Solution :
- C’est un agrandissement car nous observons que EF = 3,64 cm et E’F’ = 1,46 cm.
donc comme
alors k<0 donc k= – 0,4.
Avez-vous assimilé ce cours sur les homothéties en 3ème ?
Résumé-Quiz
0 questions correctes sur 5
Questions:
- 1
- 2
- 3
- 4
- 5
Information
QCM sur les homothéties en 3ème.
Vous avez déjà rempli le questionnaire avant. Par conséquent, vous ne pouvez pas recommencer.
Quiz is loading...
You must sign in or sign up to start the quiz.
Vous devez finir le quiz suivant, avant de commencer celui-ci :
Résultats
0 questions sur 5 répondues correctement
Votre temps:
Temps écoulé
Vous avez atteint 0 points sur 0 , (0)
| Score moyen |
|
| Votre score |
|
Categories
- Not categorized 0%
- 1
- 2
- 3
- 4
- 5
- Répondu
- Examiner
-
Question 1 sur 5
On considère l’homothétie de centre O dont la figure violette est l’image de la figure bleu.
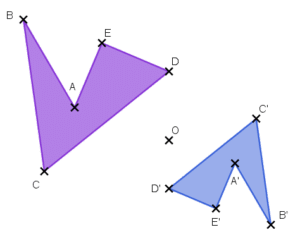
Que peut-on dire sur le rapport k de cette homothétie ?
Exact
Inexact
-
Question 2 sur 5
Soit une homothétie donc le rapport est k = – 3 ,2.
Nous pouvons affirmer que :
Exact
Inexact
-
Question 3 sur 5
Soit une homothétie donc le rapport est k = 0,76.
Nous pouvons affirmer que :
Exact
Inexact
-
Question 4 sur 5
On considère l’homothétie de centre L dont le polygone ROSE a pour image le polygone NUIT.
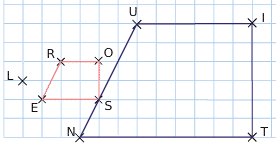
Quelle est la valeur du rapport k de cette homothétie ?
(utiliser la virgule , et pas le . point pour saisir les nombres décimaux).
- Le rapport de cette homothétie est k= (3).
Exact
Inexact
-
Question 5 sur 5
On considère l’homothétie de centre O dont le polygone ABCDE a pour image le polygone A’B’C’D’E’.
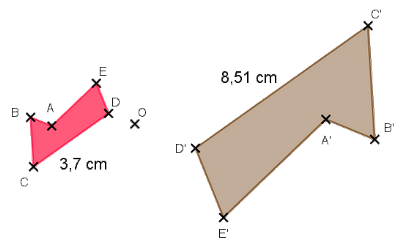
Quelle est la valeur du rapport k de cette homothétie ?
(utiliser la virgule , et pas le . point pour saisir les nombres décimaux).
- Le rapport de cette homothétie est k= (-2,3, 2.3).
Exact
Inexact
Notez Mathématiques Web !
Votre avis est précieux pour nous aider à améliorer l'application