La dérivée d’une fonction à travers un cours de maths en 1ère à assimiler.
Cette leçon fait intervenir les notions suivantes :
– définition de la dérivée en un point;
– aspect graphique de la dérivée;
– taux d’accroissement;
– dérivée d’une fonction usuelle;
– dérivée d’une somme;
– dérivée d’un produit;
– dérivée d’un quotient.
Ce document a été rédigé par un enseignant de l’éducation nationale.
I. Nombre dérivé et dérivée d’une fonction
f est une fonction définie sur un intervalle I.
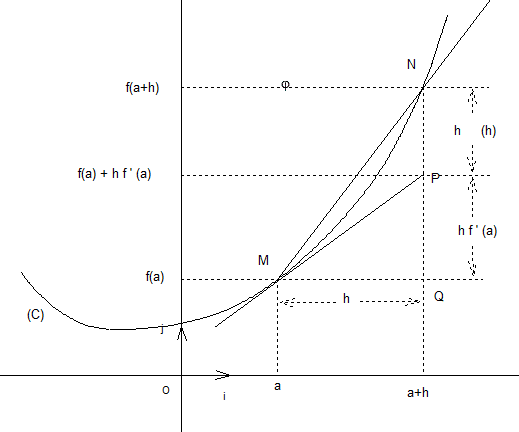
La courbe (C) ci-dessous est la représentation graphique de f dans un repère orthonormal .
M et N sont deux points de (C) d’abscisses respectives et
où
.
Si f est une fonction définie sur un intervalle I et si .
Lorsqu’il existe un nombre réel d tel que, pour tout réel h proche de 0, on ait:
On dit que la fonction f est dérivable en a et que d = f ‘(a) est le nombre dérivé de f en a.
Si f est une fonction définie sur un intervalle I et si aI.
Lorsqu’il existe un nombre réel d tel que, pour tout réel xI et proche de a, on ait:
On dit que la fonction f est dérivable en a et que d = f ‘(a) est le nombre dérivé de f en a.
II. Fonction dérivable sur un intervalle I
On dit que f est dérivable sur un intervalle I lorsqu’elle est dérivable en tout point de I
Remarques sur les notations et les « manies des physiciens »
Les physiciens expriment la différence h = x – a par la le symbole (accroissement de la variable x au voisinage du point a) et la différence f(x) – f(a) par
( accroissement correspondant entre les images de x et de a qu’ils assimilent aux ordonnées y).
Avec ces notations, ils écrivent alors au voisinage de a: .
Historiquement, la notation est due à Newton et la notation différentielle
provient de Leibniz.
III. Equation de la tangente et approximation affine de f au voisinage de x = a
La tangente (MP) à la courbe (C) en M d’abscisse a existe.Elle a pour coefficient directeur m = f ‘(a).Son équation est donc de la forme: y = mx + p, où m = f ‘(a) et son ordonnée à l’origine p est à calculer.
Pour cela, il suffit d’écrire que (MP) passe par M( a ; f(a) ).On a donc:
Ceci donne:
Donc y = f ‘(a) x + f(a) – a f ‘(a) que l’on écrit souvent sous l’une des formes, plus faciles à retenir:
ou
.
Donc, la tangente (MP) à la courbe (C) en M est la représentation graphique de la fonction affine g:
Montrons que cette fonction affine est une approximation de la fonction f lorsque x est proche de a.
En effet, l’ordonnée du point P d’abscisse x = a + h est: .
Elle s’écrit aussi: , c’est à dire:
.
Or, f(a+h) = f(a) + h f ‘(a) + h (h) avec
.
On en déduit que, lorsque h est voisin de zéro, on a: f(a+h) f(a) + h f ‘(a).
On peut donc conclure que, lorsque x est voisin de a, la fonction affine est une approximation de la fonction .
On peut même montrer, mais nous l’admettrons ici, que c’est la meilleure approximation affine de f au voisinage de a.
IV.La dérivée des fonctions usuelles.
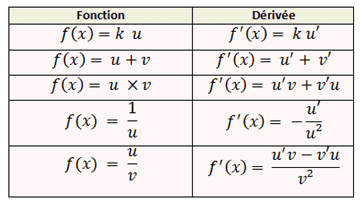
V.Les formules de dérivation