Corrigé des exercices sur les suites numériques en 1ère.

EXERCICE 1 :

On a :

$u_0=2\times 0+3=3$
$u_1=2\times 1+3=5$
$u_2=2\times 2+3=7$

Donc $u_0=3, u_1=5$ et $u_2=7$ .

EXERCICE 2 :

On a :

$u_0=\frac{0+1}{2\times 0-3}=-\frac{1}{3}$
$u_{10}=\frac{10+1}{2\times 10-3}=\frac{11}{17}$

Donc $u_0=-\frac{1}{3}$ et $u_{10}=\frac{11}{17}$ .

EXERCICE 3 :

On a :

$u_{n+1}=2(n+1)-1=2n+1+2=2n+3=u_n+2$
$u_{n-1}=2(n-1)-1=2n-3=u_n-4$
$u_{2n}=2\times 2n-1=4n-1=2(2n)-1=u_{n+1}$
$u_{n+1}=2(n+1)-1=2n+3=u_n+2$

Donc $u_{n+1}=u_n+2, u_{n-1}=u_n-4, u_{2n}=u_{n+1}$ et $u_{n+1}=u_n+2$ .

EXERCICE 4 :

1) On a :

$u_1=\frac{2\times 2-2}{2-3}=2$
$u_2=\frac{2\times 2-2}{2-3}=2$

Donc $u_2=2$ et $u_2=2$ .

2) En calculant les termes suivants, on trouve :

$u_3=-\frac{2}{5} \\\\ u_4=-6 \\\\ u_5=\frac{2}{5} \\\\ u_6=-\frac{2}{5} \\\\ u_7=\frac{2}{5} \\\\ u_8=-\frac{2}{5} \\\\ u_9=\frac{2}{5} \\\\ u_{10}=-\frac{2}{5} \\\\ u_{11}=2$

Donc $u_{15}=-\frac{2}{5}$ à $10^{-2}$ près.

EXERCICE 5 :

En lisant graphiquement les valeurs de f, on a :

$u_0=1 \\\\ u_1=4 \\\\ u_2=3 \\\\ u_3=0 \\\\ u_4=-5$

Donc $u_0=1, u_1=4, u_2=3, u_3=0$ et $u_4=-5$ .

EXERCICE 6 :

1) On a :

$u_n=u_0+nr=-3+2n$

Donc $u_n=-3+2n$ .

2) On a :

$u_{20}=-3+2\times 20=37$

Donc $u_{20}=37$ .

EXERCICE 7 :

a) On a :

$u_{n+1}=u_n-4=u_{n-1}-8$

Donc la suite $(U_n)$ est arithmétique de raison -4.

b) On a :

$v_{n+1}=-(n+1)+3=-n+2=-v_n+5$

Donc la suite $(V_n)$ est arithmétique de raison 5.

c) On a :

$w_{n+1}=(n+1)^2-3=n^2+2n+1-3=w_n+2n+1$

Donc la suite $(W_n)$ n’est pas arithmétique.

EXERCICE 8 :

a) On a :

$u_{n+1}=\frac{u_n}{2}=\frac{u_{n-1}}{2^2}=\dots=\frac{u_0}{2^{n+1}}=\frac{2}{2^{n+1}}=\frac{1}{2^n}$

Donc la suite $(U_n)$ est géométrique de raison $\frac{1}{2}$ .

b) On a :

$v_{n+1}=-3^{n+1}=(-3)^n\times (-3)=-v_n\times 3$

Donc la suite $(V_n)$ est géométrique de raison $-3$ .

c) On a :

$w_{n+1}=\frac{1}{4^{n+1}}=\frac{1}{4^n\times 4}=\frac{1}{4^n}\times \frac{1}{4}=\frac{1}{4^n}\times \frac{1}{4^n}\times \frac{1}{4}=\frac{w_n}{4}$

Donc la suite $(W_n)$ est géométrique de raison $\frac{1}{4}$ .

EXERCICE 9 :

1) On a :

$u_0=1$ (tout le gâteau est dans l’assiette)
$u_1=\frac{1}{2}$ (après le premier service, il reste la moitié)
$u_2=\frac{1}{2}\times \frac{1}{2}=\frac{1}{4}$ (après le deuxième service, il ne reste plus que le quart)

Donc $u_0=1$ et $u_1= \frac{1}{2}$ .

2) En se servant à chaque fois de la moitié de ce qui reste, Yacine divise par 2 la proportion de gâteau qui reste dans l’assiette, c’est-à-dire que la raison de la suite $(U_n)$ est $\frac{1}{2}$ .

EXERCICE 10 :

a) On a :

$u_{n+1}-u_n=(n+1)^2+2(n+1)-n^2-2n-4n-8=2n+3>0$

Donc la suite $(u_n)$ est strictement croissante.

b) On a :

$u_{n+1}-u_n=\frac{4}{n+2}-\frac{4}{n+1}=\frac{4n+4}{(n+2)(n+1)}<0$

Donc la suite $(u_n)$ est strictement décroissante.

c) On a :

$u_{n+1}-u_n=-5^{n+1}+5^n=-4\times 5^n<0$

Donc la suite $(u_n)$ est strictement décroissante.

EXERCICE 11 :

1) On a :

$\frac{u_{n+1}}{u_n}=\frac{2^{n+1}}{n+1}\times \frac{n}{2^n}=\frac{2}{1+\frac{1}{n}}\longrightarrow 2$

Donc la suite $(U_n)$ est géométrique de raison 2.

2) On a :

$\frac{2n}{n+1}>1\quad \Leftrightarrow \quad 2n>n+1\quad \Leftrightarrow \quad n>1$

Donc l’inéquation est vérifiée pour tout entier n plus grand que 1.

3) La raison de la suite $(u_n)$ est strictement positive, donc cette suite est strictement croissante.

EXERCICE 12 :

1) On a :

$u_n=1,5(u_{n-1})=1,5^2(u_{n-2})=\dots=1,5^n$

Donc $u_n=1,5^n$ .

2) On a :

$u_{10}=1,5^{10}=576,75$

Donc la 10ème poupée mesure 576,75 cm (ou 5,7675 m).

3) Si on empile les poupées, leur hauteur est égale à la somme de leur taille, c’est-à-dire :

$- 1+1,5+1,5^2+\dots+1,5^9 \approx 29,1499$

Donc la pile de 10 poupées a une hauteur d’environ 29,1499 cm.

EXERCICE 13 :

1) On a :

$u_0=2\times 0 +3=3 \\\\ u_1=2\times 1 +3=5 \\\\ u_2=2\times 2 +3=7$

Donc u_0=3, u_1=5 et u_2=7.

2) On a :

$u_0=\frac{0+1}{2\times 0-3}=-\frac{1}{3} \\\\ u_{10}=\frac{10+1}{2\times 10-3}=\frac{11}{17}$

Donc $u_0=-\frac{1}{3}$ et $u_{10}=\frac{11}{17}$ .

3) On a :

$u_0=2^0-1=0 \\\\ u_1=2^1-1=1 \\\\ u_2=2^2-1=3 \\\\ u_3=2^3-1=7 \\\\ u_4=2^4-1=15$

Donc $u_0=0, u_1=1, u_2=3, u_3=7$ et $u_4=15$ .

4) On a :

$u_{n+1}=2(n+1)-1=2n+1+2=2n+3=u_n+2 \\\\ u_{n-1}=2(n-1)-1=2n-3=u_n-4 \\\\u_{2n}=2^{2n}-1=(2^n)^2-1=(2^n-1)(2^n+1)=u_n(u_n+2) \\\\ u_{n+1}=2(n+1)-1=2n+3=u_n+2$

Donc $u_{n+1}=u_n+2, u_{n-1}=u_n-4, u_{2n}=u_n(u_n+2)$ et $u_{n+1}=u_n+2$ .

5) On a :

$u_{n+1}=(n+1)^2+1 \\\\u_{n-1}=(n-1)^2+1 \\\\u_{2n}=4n^2+1 \\\\ u_{n+1}=n^2+2n+1+1=(n+1)^2$

Donc $u_{n+1}=(n+1)^2+1, u_{n-1}=(n-1)^2+1, u_{2n}=4n^2+1$ et $u_{n+1}=(n+1)^2+1$ .

EXERCICE 14 :

1) On a :

$u_1=\frac{1}{2}\times 200+80=180 \\\\u_2=\frac{1}{2}\times 180+80=140$

Donc u_1=180 et u_2=140.

2) On a :

$u_{n+1}=\frac{1}{2}\times u_n+80$

Donc la suite $(u_n)$ est une suite arithmético-géométrique, mais il n’y a pas de forme explicite pour ses termes.

EXERCICE 15 :

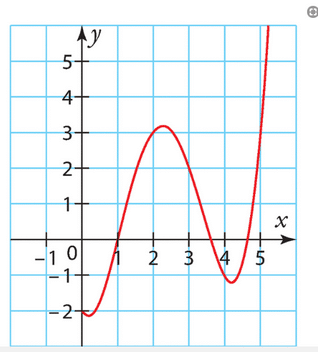
En lisant graphiquement les valeurs de f, on a :

$\\\\u_0=1 \\\\u_1=2 \\\\ u_2=5 \\\\u_3=10 \\\\ u_4=17$

Donc $u_0=1, u_1=2, u_2=5, u_3=10$ et $u_4=17$ .

EXERCICE 16 :

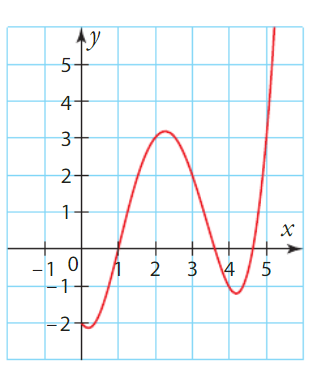
En lisant graphiquement les valeurs de f, on a :

$v_0=1 \\\\ v_1=4 \\\\ v_2=17 \\\\ v_3=58 \\\\v_4=175$

Donc $v_0=1, v_1=4, v_2=17, v_3=58$ et $v_4=175$ .

EXERCICE 17 :

1) On a :

$u_1=u_0+4=6$
$u_2=u_1+4=10$
$u_3=u_2+4=14$

Donc $u_1=6, u_2=10$ et $u_3=14$ .

2) On a :

$u_n=u_0+4n=2+4n$

Donc $u_n=2+4n$ .

EXERCICE 18 :

a) On a :

$u_{n+1}-u_n=2n+2>0$

Donc la suite $(u_n)$ est strictement croissante.

b) On a :

$u_{n+1}-u_n=\frac{4}{n+2}-\frac{4}{n+1}=-\frac{4}{(n+2)(n+1)}<0$

Donc la suite $(u_n)$ est strictement décroissante.

c) On a :

$u_{n+1}-u_n=-5^{n+1}+5^n=-4\times 5^n<0$

Donc la suite $(u_n)$ est strictement décroissante.

EXERCICE 19 :

1) On a :

$\frac{u_{n+1}}{u_n}=\frac{2^{n+1}}{n+1}\times \frac{n}{2^n}=\frac{2}{1+\frac{1}{n}}\longrightarrow 2$

Donc la suite $(U_n)$ est géométrique de raison 2.

2) On a :

$\frac{2n}{n+1}>1\quad \Leftrightarrow \quad 2n>n+1\quad \Leftrightarrow \quad n>1$

Donc l’inéquation est vérifiée pour tout entier n plus grand que 1.

3) La raison de la suite $(u_n)$ est strictement positive, donc cette suite est strictement croissante.

EXERCICE 20 :

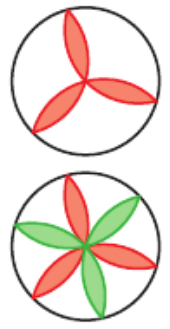
1) La rosace à l’étape 2 ressemble à ça :

Donc $u_1=6$ .

2) On a :

$u_1=6$

$u_2=6+3=9$

Donc $u_1=6$ et $u_2=9$ .

3) On peut remarquer que pour passer de l’étape n à l’étape n+1, on ajoute 4 pétales (un entre chaque paire de pétales déjà existants), donc la relation entre $u_n$ et $u_{n+1}$ est :

$u_{n+1}=u_n+4$

Donc la suite $(u_n)$ est arithmétique de raison 4.

4) On peut conjecturer que la limite de la suite est l’infini, car à chaque étape, le nombre de pétales est multiplié par environ 4/3.

5) On a :

$v_0=0,1\times 1=0,1$
$v_1=0,1\times 5=0,5$

Donc $v_0=0,1$ et $v_1=0,5$ .

6) On peut remarquer que pour passer de l’étape n à l’étape n+1, on multiplie l’épaisseur par 2 (car on plie en deux chaque couche), donc la relation entre $v_n$ et $v_{n+1}$ est :